
- •1.Разделы дисциплины и виды занятий (тематический план)
- •2. Содержание разделов дисциплины в третьем семестре
- •Раздел 16.
- •Раздел 17.
- •Раздел 18.
- •Раздел 19
- •Раздел 20
- •Раздел 21 Элементы вариационного исчисления и
- •3. Учебно-методическое обеспечение дисциплины
- •4. Методические рекомендации по организации изучения математики
- •Контрольные мероприятия
- •5. Рекомендуемый перечень тем практических занятий
- •6. Лабораторные работы
- •7. Темы, выносимые на самостоятельное изучение тема №1 операционное исчисление и задачи тау, тоэ.
- •Тема №2 вычисление вероятностей в классической схеме сиспользованием формул комбинаторики. Геометрические вероятности.
- •Тема №3 приложение теорем умножения и сложения вероятностей, формулы байеса.
- •Тема №4 числовые характеристики биноминального, равномерного, показательного и нормального распределений, распределения пуассона
- •Тема №5 частные случаи систем двух случайных величин
- •Тема №6 вычисление доверительного интервала
- •Тема №7 статистические оценки параметров распределения. Методы расчета сводных характеристик. Проверка статистических гипотез
- •Заключение
- •394026 Воронеж, Московский просп.,14
6. Лабораторные работы
Неде- ля семе- стра
|
Наименование лабораторной работы |
Объ- ем ча- сов |
В том числе в интерактивной форме (ИФ) |
Виды контроля |
|
3 семестр |
18 |
18 |
|
||
1-5 |
Решение задач уравнений математической физики |
6 |
6 |
отчет |
|
7 |
Решение задач теории вероятности |
2 |
2 |
отчет |
|
9 |
Решение задач математической статистики |
2 |
2 |
отчет |
|
11-17 |
Решение задач вариационного исчисления |
8 |
8 |
отчет |
|
7. Темы, выносимые на самостоятельное изучение тема №1 операционное исчисление и задачи тау, тоэ.
Литература: [1], [4].
Пример
. В контуре,
состоящем из последовательно соединенных
катушки индуктивности
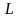 ,
конденсатора емкости
,
конденсатора емкости
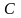 и резистора сопротивления
и резистора сопротивления
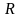 в момент времени
в момент времени
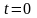 включается Э.Д.С.
включается Э.Д.С.
 (рис. 1). В этот момент ток в контуре и
заряд конденсатора равны нулю. Найти
законы изменения напряжения на
конденсаторе
(рис. 1). В этот момент ток в контуре и
заряд конденсатора равны нулю. Найти
законы изменения напряжения на
конденсаторе
 и тока в цепи
и тока в цепи
 .
.
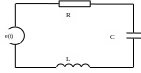
Рис. 1
Решение. Поскольку элементы цепи соединены последовательно, то из закона Кирхгофа имеем равенство
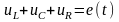 (1)
(1)
где соответствующие напряжения выражаются через ток в цепи по формулам:
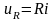 ,
(2) (2)
,
(2) (2)
 (3)
(3)
 (4)
(4)
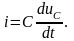 (5)
(5)
В
силу (2),(3) и (5) имеем
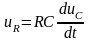 ,
,
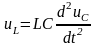 и поэтому из (1) получаем дифференциальное
уравнение
и поэтому из (1) получаем дифференциальное
уравнение
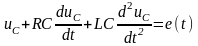 (6)
(6)
с начальными условиями
 (7)
(7)
Рассмотрим
случай постоянной Э.Д.С.
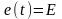 .
Совершая преобразование Лапласа с
учетом (7) получим:
.
Совершая преобразование Лапласа с
учетом (7) получим:

В
нашей задаче от дифференциального
уравнения (6) перейдем к операторному
уравнению
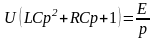 ,
откуда находим изображение напряжения
на конденсаторе:
,
откуда находим изображение напряжения
на конденсаторе:
 (8)
(8)
В квадратном трехчлене выделим полный квадрат:
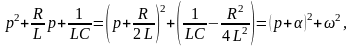
где
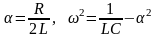 .
Раскладывая дробь в (8) на сумму простейших
дробей, получим
.
Раскладывая дробь в (8) на сумму простейших
дробей, получим
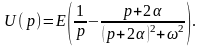 (9)
(9)
Далее рассмотрим различные возможные случаи.
а)
Если
 (сверхпроводимость), то
(сверхпроводимость), то
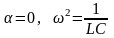 и выражение (9) примет вид
и выражение (9) примет вид
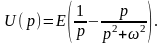 Переходя от изображения к оригиналу,
получим искомое напряжение:
Переходя от изображения к оригиналу,
получим искомое напряжение:
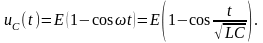
Отсюда в силу (5) находим ток в контуре:
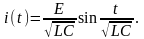
Таким образом, при имеют место гармонические колебания тока в контуре и напряжения
б)
Если сопротивление мало ( ),
то
),
то
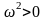 и
и
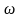 можно считать действительным положительным
числом. В этом случае в формуле (9)
выражение в скобках имеет следующий
оригинал
можно считать действительным положительным
числом. В этом случае в формуле (9)
выражение в скобках имеет следующий
оригинал
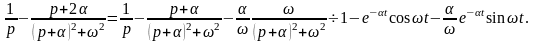
Получаем искомое напряжение на конденсаторе:
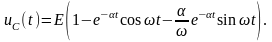
Отсюда в силу (5) находим ток в контуре:
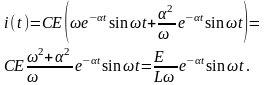
В
этом случае имеют место затухающие
колебания тока в контуре и напряжения
на конденсаторе, причем напряжение на
конденсаторе стремится к
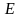 ,
а ток к нулю.
,
а ток к нулю.
в)
Если
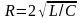 ,
то
,
то
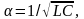
 и выражение (9) примет вид
и выражение (9) примет вид
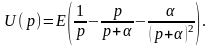 переходя от изображения к оригиналу,
получим искомое напряжение:
переходя от изображения к оригиналу,
получим искомое напряжение:
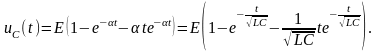
Отсюда в силу (5) находим ток в контуре:
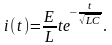
В этом случае колебания в контуре отсутствуют, напряжение на конденсаторе стремится к , а ток в цепи стремится к нулю.
г)
Если сопротивление велико (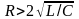 ),
то
),
то
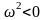 .
Обозначим
.
Обозначим
 ,
где
,
где
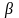 можно считать действительным
можно считать действительным
положительным числом. В этом случае в формуле (9) выражение в скобках имеет следующий оригинал
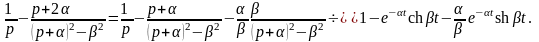
Получаем искомое напряжение на конденсаторе:

Отсюда в силу (5) находим ток в контуре:
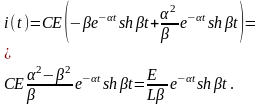
В
этом случае колебания в контуре
отсутствуют, напряжение на конденсаторе
стремится к
,
а ток в цепи стремится к нулю, так как
 .
.
Замечание. Операционный метод используется и при решении интегро-дифференциальных уравнений. В нашей задаче можно вначале находить ток , для которого в силу уравнений (1) (4) имеем
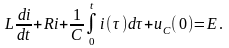 (10)
(10)
Если
 ,
то с учетом начальных условий (7) и
свойства интегрирования оригинала
получим
,
то с учетом начальных условий (7) и
свойства интегрирования оригинала
получим
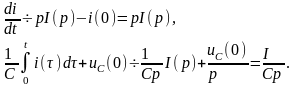
Производим преобразование Лапласа уравнения (10):
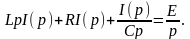
Отсюда получаем
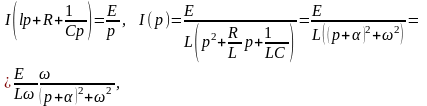 (11)
(11)
где
 Далее рассмотрим различные возможные
случаи.
Далее рассмотрим различные возможные
случаи.
а)
Если
(сверхпроводимость), то
и выражение (11) примет вид
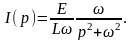 Переходя от изображения к оригиналу,
получим искомый ток:
Переходя от изображения к оригиналу,
получим искомый ток:

Таким образом, при имеют место гармонические колебания тока в контуре.
б)
Если сопротивление мало (
),
то
и
можно считать действительным положительным
числом. В этом случае
 .
.
В
этом случае имеют место затухающие
колебания тока в контуре, так как
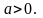
в)
Если
,
то
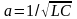 ,
и выражение (11) примет вид
,
и выражение (11) примет вид
 .
Переходя от изображения к оригиналу,
получим искомое значение тока:
.
Переходя от изображения к оригиналу,
получим искомое значение тока:

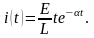
В этом случае колебания в контуре отсутствуют, ток в цепи стремится к нулю, так как
г)
Если сопротивление велико
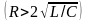 ,
то
.
,
то
.
Обозначаем , где можно считать действительным положительным числом. В этом случае выражение (11) имеет следующий оригинал

В этом случае колебания в контуре отсутствуют, ток в цепи стремится к нулю, так как .
Форма отчетности: устный опрос
