5.2. Пример
Для взвешенного орграфа найти кратчайший путь из вершины s в вершину t.
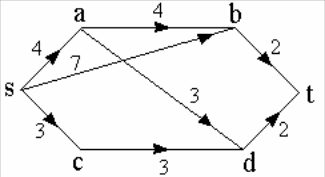
Рис. 17
1. Помечаем в соответствии с алгоритмом вершины графа:
l(s) = 0 ,
l(a) = ∞ ,
l(b) = ∞ ,
l(c) = ∞ ,
l(d) = ∞ ,
l(t) = ∞ .
Вершине s приписываем постоянную пометку, т.е. p = s.
2. Из вершины s помечаем остальные вершины:
l(a) = min {∞, 0 + 4} = 4,
l(b) = min {∞, 0 + 7} = 7,
l(c) = min {∞, 0 + 3} = 3,
l(d) = ∞ ,
l(t) = ∞ .
У вершин a, b, и с уменьшились пометки, следовательно
Q(a) = s, Q(b) = s, Q(c) = s.
Вершине c приписываем постоянную пометку, т.е. p = c. Пометка Q(с)=s также становится постоянной.
3. Из вершины c помечаем остальные вершины:
l(a) = min {4, 3 + ∞} = 4,
l(b) = min {7, 3 + ∞} = 7,
l(d) = min {∞, 3 + 3} = 6,
l(t) = ∞ .
У вершины d уменьшилась пометка, следовательно Q(d) = c.
Вершине a приписываем постоянную пометку, т.е. p = a. Пометка Q(a)=s становится постоянной.
4. Из вершины а помечаем остальные вершины:
l(b) = min {7, 4 + 4} = 7,
l(d) = min {6, 4 + 3} = 6,
l(t) = ∞ .
Вершине d приписываем постоянную пометку, т.е. p = d.. Пометка Q(d)=c становится постоянной.
5. Из вершины d помечаем остальные вершины:
l(b) = min {7, 6 + ∞} = 7,
l(t) = min {∞, 6 + 2} = 8,
У вершины t уменьшилась пометка, следовательно Q(t) = d.
Вершине b приписываем постоянную пометку, т.е. p=b. Пометка Q(b)=s становится постоянной.
6. Из вершины b помечаем вершину t:
l(t) = min {8, 7 + 2} = 8.
Метки l(t) и Q(t)=d становятся постоянными.
7. Восстанавливаем по меткам Q кратчайший путь из s в t:
Путь scdt длиной 8.
Работу алгоритма можно проиллюстрировать таблицей:
Вершина |
1 |
2 |
3 |
4 |
5 |
6 |
s |
0 |
- |
- |
- |
- |
- |
a |
∞ |
4 |
4 |
- |
- |
- |
b |
∞ |
7 |
7 |
7 |
7 |
- |
c |
∞ |
3 |
- |
- |
- |
- |
d |
∞ |
∞ |
6 |
6 |
- |
- |
t |
∞ |
∞ |
∞ |
∞ |
8 |
8 |
5.3. Упражнения
Определить кратчайший путь от вершины s до вершины t с использованием алгоритма Дейкстры.
а б
в г
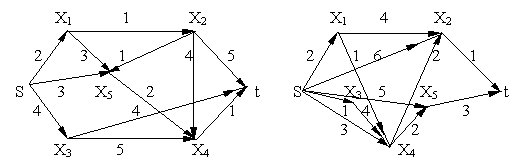
д е
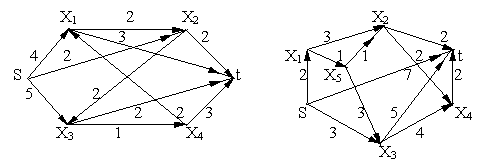
ж з
Рис. 18
6. Определение кратчайших путей между всеми парами вершин графа. Алгоритм флойда