
- •Решение задач теории графов методические указания
- •1. Определение метрических характеристик графов
- •1.1. Теоретические сведения
- •1.2. Пример
- •1.3. Упражнения
- •2. Определение сильных компонент графа
- •2.1. Теоретические сведения
- •2.2. Пример
- •2.3. Задачи для самостоятельного решения
- •3. Построение остовных деревьев графа
- •3.1. Теоретические сведения
- •3.2. Примеры решения задач
- •Решение Кратчайший остов для данного графа имеет следующий вид:
- •Алгоритм Прима
- •3.3. Упражнения
- •4. Построение эйлеровых и гамильтоновых циклов в графе
- •4.1. Теоретические сведения
- •4.2. Примеры решения задач
- •4.3. Упражнения
- •5. Определение кратчайшего пути между двумя вершинами графа. Алгоритм дейкстры
- •5.1. Теоретические сведения
- •5.2. Пример
- •5.3. Упражнения
- •6. Определение кратчайших путей между всеми парами вершин графа. Алгоритм флойда
- •6.1. Теоретические сведения
- •6.2. Пример
- •6.3. Упражнения
- •7. Определение максимального потока в транспортной сети
- •7.1. Теоретические сведения
- •Алгоритм Форда-Фалкерсона включает следующие шаги: а. Расстановка пометок
- •7.3 Упражнения
- •Библиографический список
- •Содержание
- •Решение задач теории графов методические указания
- •394026 Воронеж, Московский просп., 14
1.2. Пример
Определить метрические характеристики графа
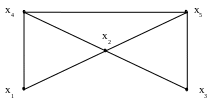
Рис. 1
Решение. Метрические характеристики определяются следующим образом:
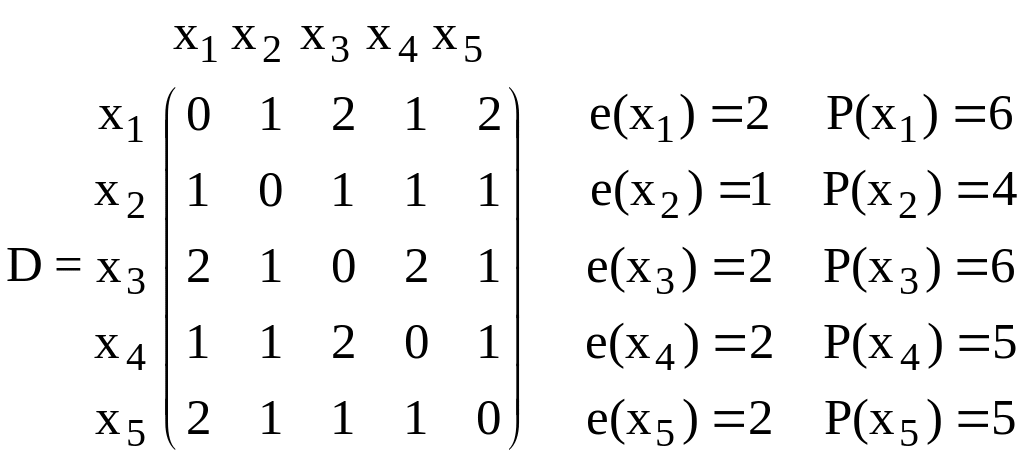
Радиус
графа равен 1, диаметр равен 2. Центр
графа - вершина
![]() ;
Медиана графа - вершина
.
;
Медиана графа - вершина
.
1.3. Упражнения
1. Определить метрические характеристики неориентированных графов
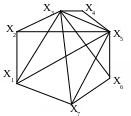
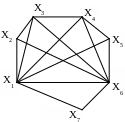
а б
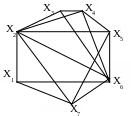
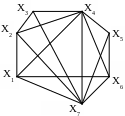
в г
Рис. 2
2. Определить метрические характеристики ориентированных графов
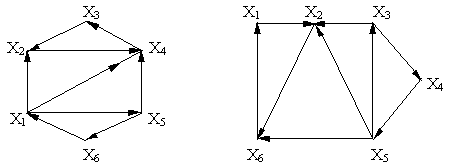
Рис. 3
2. Определение сильных компонент графа
2.1. Теоретические сведения
Орграф называется сильно связным, если любые две его вершины взаимно достижимы, односторонне связным, если для любых двух вершин по крайней мере одна достижима из другой и слабо связным, если связным является лежащий в его основе неорграф.
Сильной компонентой орграфа называется его максимальный сильно связный подграф, подграф, не содержащийся ни в каком другом сильно связном подграфе этого графа.
Для определения сильных компонент графа необходимо:
Построить матрицу достижимости графа. Матрицей достижимости графа с n вершинами называется квадратная матрица R порядка n, элементы которой определяются следующим образом:
![]()
2. Построить матрицу контрдостижимости графа. Матрицей контрдостижимости графа с n вершинами называется квадратная матрица Q порядка n, элементы которой определяются следующим образом:
![]()
![]()
Матрицу контрдостижимости можно определить по матрице достижимости следующим образом:
3. Построить матрицу сильной связности графа. Матрицей сильной связности орграфа с n вершинами называется квадратная матрица S порядка n, элементы которой определяются следующим образом:
![]()
Матрицу сильной связности можно определить следующим образом:
![]()
где * - операция поэлементного умножения матриц.
4.
По матрице сильной связности выделить
сильные компоненты графа. Если вершины
принадлежат одной сильной компоненте
орграфа, то
![]() .
При этом строки (столбцы), соответствующие
этим вершинам в матрице S, одинаковы.
.
При этом строки (столбцы), соответствующие
этим вершинам в матрице S, одинаковы.
2.2. Пример

Рис. 4
Решение. Для данного графа матрицы R, Q и S имеют вид:

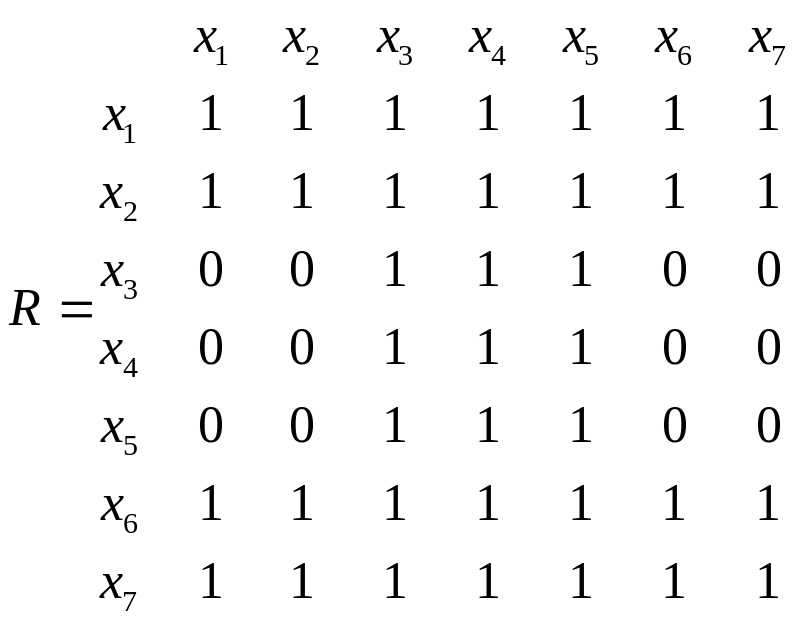

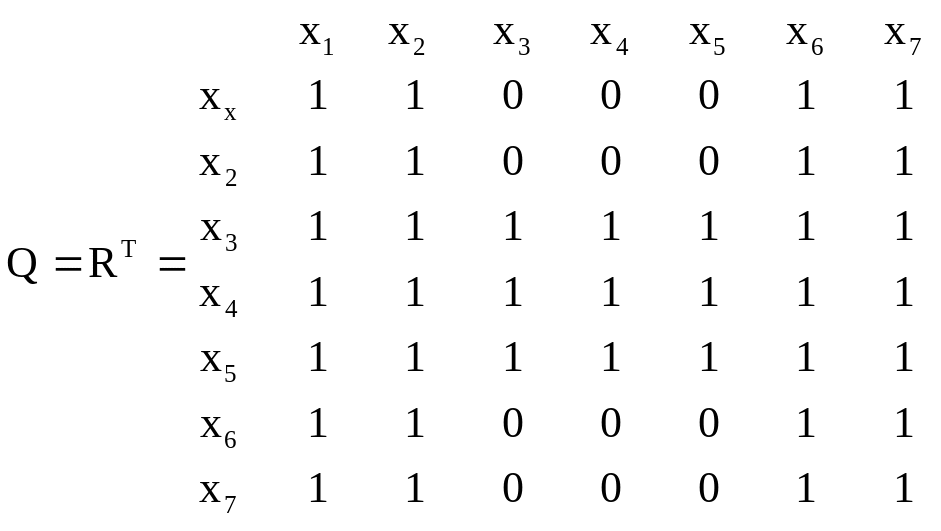

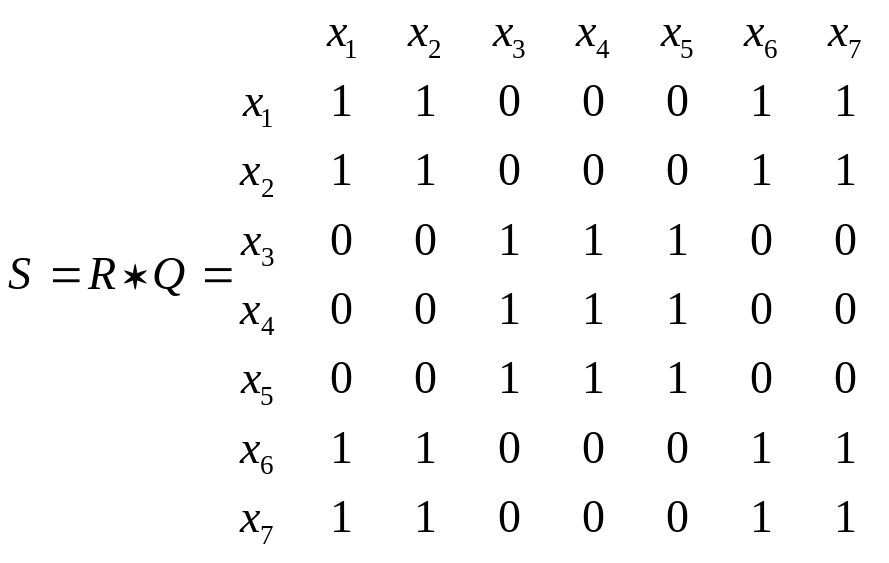
В соответствии с матрицей S сильные компоненты графа:
х1, х2, х6,х7 –первая сильная компонента;
х3, х4, х5 - вторая сильная компонента.
2.3. Задачи для самостоятельного решения
Определить сильные компоненты графов.
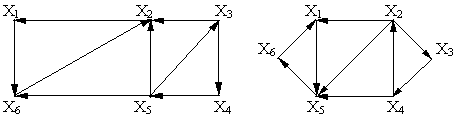
а б
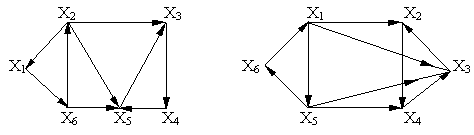
в г
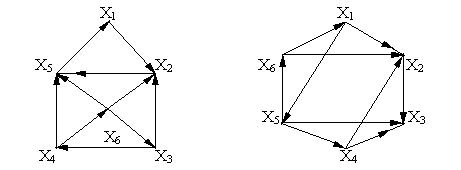
д е
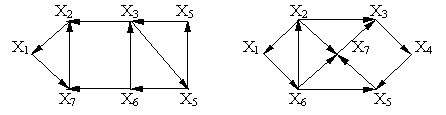
ж з
Рис. 5
