3. Построение остовных деревьев графа

3.1. Теоретические сведения

Связный ациклический граф, имеющий не менее двух вершин, называется деревом. Ориентированным деревом называется орграф без циклов, в котором имеется вершина x₀, из которой существует только один ориентированный путь в любую другую вершину. Деревом графа G называется любой его связный ациклический подграф. называется остовным деревом (остовом) Т графа G. При этом ребра остовного дерева T называются ветвями, а ребра графа G, не принадлежащие остову T - хордами. На рис 6. а представлен граф G, на рис. 6. б - одно из его деревьев, на рис. 6 в, г - два остова T₁ и T₂ графа G, на рис. 6. д - остовное 2 - дерево (лес) графа G.

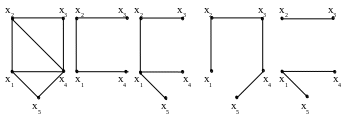
а б в г д

Рис. 6

Очевидно, что в любом графе существует остов, причем в общем случае остов может быть выделен не единственным способом.

Для построения произвольного остова связного графа могут быть использованы две стратегии: поиск в глубину и поиск в ширину.

Опишем алгоритм поиска в глубину (этот метод стал одной из основных методик проектирования графовых алгоритмов). Поиск начинается с некоторой фиксированной вершины x_o, например, с висячей. Затем выбирается вершина x₁, смежная с x_o. После этого выбирается вершина x₂, смежная с x₁, и т.д. Ещё не просмотренные вершины будем условно называть новыми. Если на k-м шаге поиска для вершины x_k существует новая вершина x_k+1, то она выбирается (перестаёт быть новой) и поиск продолжается от вершины x_k+1. Если же для вершины x_k новых вершин не существует, осуществляется возврат к вершине, из которой мы попали в x_k, и поиск осуществляется от неё. Процесс продолжается до тех пор, пока не будет произведён возврат в вершину x_o. В процессе поиска вершины соединяют рёбрами.

Поиск в ширину отличается от поиска в глубину тем, что выбор очередной вершины происходит путём просмотра не одной, а всех смежных вершин из списка новых.

Рассмотренные алгоритмы могут быть использованы для построения всех остовных деревьев графа.

При конструкторском и топологическом проектировании РЭА и ЭВА, создании вычислительных сетей важное значение имеет задача определения кратчайшего остова (остова минимального веса) взвешенного графа. Кратчайшим остовом взвешенного графа G будем называть остов, у которого сумма весов всех ребер наименьшая.

Для построения кратчайшего остова графа используются алгоритмы Краскала и Прима.

Алгоритм Краскала заключается в следующем. На начальном этапе из всех ребер графа G выбирается ребро минимального веса и включается в остов. На каждом последующем i-м шаге из еще не включенных в остов ребер выбирается ребро, имеющее минимальный вес и не составляющее циклов с уже выбранными ребрами. Процесс продолжается до тех пор, пока в остов не будет включено n-1 ребро.

Алгоритм Прима отличается от алгоритма Краскала только тем, что на каждом этапе строится не просто ациклический граф, а дерево, которое в дальнейшем последовательно разрастается. При этом, если дерево уже построено, то новое ребро выбирается не из всех оставшихся ребер графа G, а только из тех, которые соединяют вершины дерева с вершинами, не включенными в . Из этих ребер выбирается ребро минимального веса. При этом необходимо следить за тем, чтобы не появлялись циклы.