6.3. Упражнения

Определить кратчайшие пути между всеми парами вершин графов с использованием алгоритма Флойда

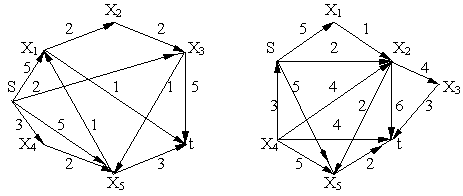
а б

в г

Рис. 20

7. Определение максимального потока в транспортной сети

7.1. Теоретические сведения

Рассмотрим граф G=(X,U), называемый в дальнейшем сетью. Пусть каждой дуге (x_i, x_j) сопоставлено положительное число c_ij , называемое пропускной способностью дуги. В сети выделяют два специальных узла, один из них называют источником (обозначим его через s), другой – стоком (обозначим его через t). Множество неотрицательных чисел f_ij , определенных на дугах (x_i,x_j), называют потоками в дугах, если выполняются следующие условия:

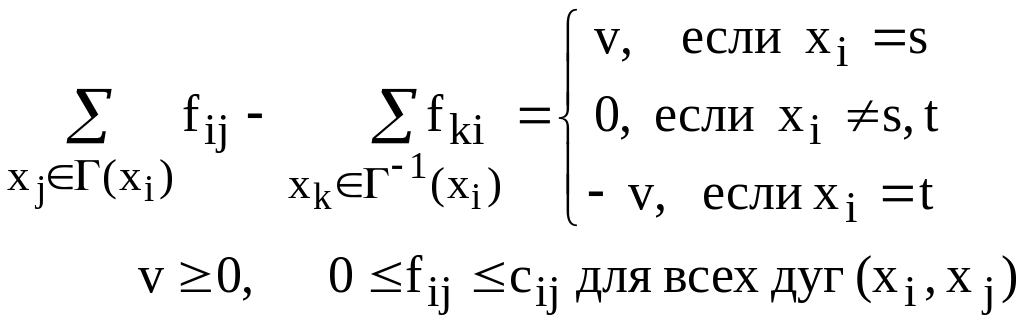
Линейные ограничения отражают тот факт, что поток, втекающий в вершину, равен потоку, вытекающему из нее, за исключением вершин, являющихся источником и стоком. При этом поток в каждой дуге не должен превышать ее пропускной способности. Величина v, равная сумме потоков по всем дугам, исходящим из источника s, или сумме потоков по всем дугам, заходящим в вершину t, называется величиной потока в сети:

Задача о максимальном потоке состоит в нахождении такого множества потоков по дугам, чтобы величина потокаv в сети была максимальной при условии отсутствия превышения пропускных способностей дуг.

Для определения максимального потока в сети можно воспользоваться алгоритмом Форда-Фалкерсона. Идея алгоритма состоит в следующем. Выбирается некоторый начальный поток из s в t и осуществляется поиск увеличивающего пути. Если увеличивающий путь найти не удаётся, выполнение алгоритма заканчивается, и текущий поток из s в t является максимальным. Если увеличивающий путь найден, то поток вдоль данного пути увеличивается до максимально возможного значения. Затем выполняется поиск нового увеличивающего пути, и т.д.

Вершина может находиться в одном из трёх состояний: вершине приписана пометка и вершина просмотрена (т.е. она имеет пометку и все смежные с ней вершины «обработаны»); пометка приписана, но вершина не просмотрена (т.е. она имеет пометку, но не все смежные с ней вершины обработаны); вершина не имеет пометки. Пометка произвольной вершины x_i состоит из двух частей и имеет один из двух видов: (+x_j, ) или (x_j, ). Часть +x_j пометки первого типа означает, что поток допускает увеличение вдоль дуги (x_j, x_i). Часть x_j пометки другого типа означает, что поток может быть уменьшен вдоль дуги (x_i, x_j). В обоих случаях  задаёт максимальную величину дополнительного потока, который может протекать от s к x_i.

Алгоритм Форда-Фалкерсона включает следующие шаги: а. Расстановка пометок

Шаг 1. Присвоить вершине s пометку (+s, (s) = ∞). Вершине s присвоена пометка и она просмотрена, все остальные вершины без пометок.

Шаг 2. Взять некоторую непросмотренную вершину с пометкой; пусть её пометка будет (x_k, (x_i)).

(I) Каждой непомеченной вершине x_j  Г (x_i), для которой f_ij < c_ij, присвоить пометку (+x_i, (x_j)), где (x_j) = min [(x_i), c_ij  f_ij ].

(II) Каждой непомеченной вершине x_j  Г^-1(x_i), для которой f_ji > 0, присвоить пометку (x_i, (x_j)), где (x_j) = min [(x_i), f_ji ]. Теперь вершина x_i и помечена, и просмотрена, а вершины x_j, пометки которым присвоены в (I) и (II), являются непросмотренными.) Обозначить каким-либо способом, что вершина x_i просмотрена.

Шаг 3. Повторять шаг 2 до тех пор, пока либо вершина t будет помечена , и тогда перейти к шагу 4, либо t будет не помечена и никаких других пометок нельзя будет расставить; в этом случае алгоритм заканчивает работу с максимальной величиной потока.

Б. Увеличение потока

Шаг 4. Положить x = t и перейти к шагу 5.

Шаг 5. (I) Если пометка в вершине x имеет вид (+z, (x)), то изменить поток вдоль дуги (z, x) с f(z, x) на f(z, x) + (t).

(II) Если пометка в вершине x имеет вид (z, (x)), то изменить поток вдоль дуги (x, z) с f(x, z) на f(x, z)  (t).

Шаг 6. Если z = s, то стереть все пометки и вернуться к шагу 1, чтобы вновь начать расставлять пометки, но используя уже улучшенный поток, найденный на шаге 5. Если z  s, то положить x = z и вернуться к шагу 5.

7.2. Пример. Найти максимальный поток от x₁ к x₉ для графа

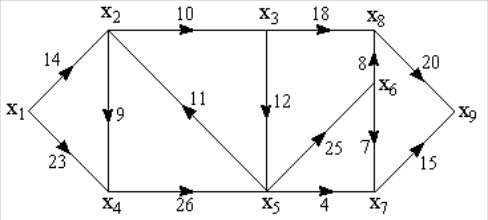
Рис. 21

Решение. В качестве начального возьмем поток с нулевыми значениями на всех дугах. Алгоритм работает следующим образом.

Шаг 1. Припишем вершине x₁ пометку (+x₁, ∞).

Шаг 2. (I) Множество вершин { x_j | x_j  Г (x₁), f_1j < c_1j , x_j не помечена} есть {x₂, x₄}, вершине x₂ приписывается пометка (+x₁, min [∞, 14 - 0]), т.е. (+x₁, 14), вершине x₄ приписывается (+x₁, min [∞, 23 - 0]), т.е. (+x₁, 23).

(II) Множество вершин { x_j | x_j  Г^-1 (x₁), f_j1 > 0, x_j непомечена} является пустым. Итак, x₁ помечена и просмотрена, x₂ и x₄ помечены и не просмотрены, а все остальные вершины не помечены. Повторяем шаг 2 и первой просматриваем вершину x₂.

(I) Множество { x_j | x_j  Г (x₂), f_2j < c_2j , x_j не помечена} есть x₃, и для x₃ пометкой будет (+x₂, min [14, 10 - 0]) = (+x₂, 10).

(II) Множество вершин { x_j | x_j  Г^-1 (x₂), f_j2 > 0, x_j не помечена} является пустым. Теперь вершины x₁ и x₂ помечены и просмотрены, а x₃ и x₄ помечены, но не просмотрены.

Беря для просмотра x₃ и повторяя шаг 2, придем к следующим пометкам:

для x₅ пометкой будет (+x₃, min [10, 12 - 0]) = (+x₃, 10),

для x₈ пометкой будет (+x₃, min [10, 18 - 0]) = (+x₃, 18).

Выбирая для просмотра x₄, найдем, что никаких пометок расставить нельзя.

Продолжая просмотр с x₅, получим следующие пометки:

пометка для x₆ будет (+x₅, min [10, 25 - 0]) = (+x₅, 10),

пометка для x₇ будет (+x₅, min [10, 4 - 0]) = (+x₅, 4),

пометка для x₉ будет (+x₇, min [4, 15 - 0]) = (+x₇, 4).

Переходя к шагам 4 и 5, получим:

x = x₉; f_{7, 9} = 0 + 4 = 4;

x = x₇; f_{5, 7} = 4;

x = x₅; f_{3, 5} = 4;

x = x₃; f_{2, 3} = 4;

x = x₂; f_{1, 2} = 4.

Вид потока в конце шага 5 и пометки вершин до их стирания на шаге 6 показаны на рис. 22. Все потоки показаны подчеркиванием. Толстыми линиями далее везде обозначены насыщенные дуги, т.е. дуги, в которых величина потока равна их пропускной способности.

Стирая пометки у вершин и возвращаясь к шагу 1 для второй итерации, получим следующие новые пометки вершин (помеченные, но не просмотренные вершины просматриваются в порядке возрастания их номеров):

Шаг 3.

Пометкой для x₁ будет (+x₁, ∞),

пометкой для x₂ будет (+x₁, min [∞, 14 - 4]) = (+x₁, 10),

пометкой для x₄ будет (+x₁, min [∞, 23 - 0] = (+x₁, 23);

теперь вершина x₁ помечена и просмотрена.

Пометкой для x₃ будет (+x₂, min [10, 10 - 4]) = (+x₂, 6),

теперь вершина x₂ помечена и просмотрена.

Пометкой для x₅ будет (+x₃, min [6, 12 - 4]) = (+x₃, 6),

Пометкой для x₈ будет (+x₃, min [6, 18 - 0]) = (+x₃, 6);

теперь вершина x₃ помечена и просмотрена; вершина x₄ также помечена и просмотрена.

Пометкой для x₆ будет (+x₅, min [6, 25 - 0]) = (+x₅, 6),

теперь вершина x₅ помечена и просмотрена.

Пометкой для x₇ будет (+x₆, min [6, 7 - 0]) = (+x₆, 6),

теперь вершина x₆ помечена и просмотрена.

Пометкой для x₉ будет (+x₇, min [6, 15 - 4]) = (+x₇, 6).

Шаги 4 и 5.

Новые потоки увеличились следующим образом:

f_{7, 9} = 4 + 6 = 10; f_{6, 7} = 0 + 6 = 6; f_{5, 6} = 0 + 6 = 6;

f_{3, 5} = 4 + 6 = 10; f_{2, 3} = 4 + 6 = 10; f_{1, 2} = 4 + 6 =10;

все остальные значения потока не изменились.

Новый вид потока и пометки вершин до стирания показаны на рис.23.

Продолжая дальше, получаем после каждого прохода алгоритма потоки и пометки, изображенные последовательно на рисунках 24  26. Алгоритм заканчивает работу, когда вершина не может быть помечена.

Поток на рис.27. является поэтому максимальным потоком со значением 29.

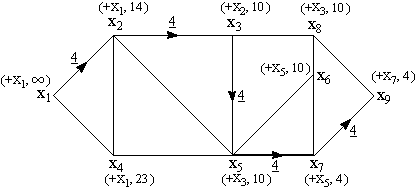
Рис.22. Потоки и пометки после первой итерации.

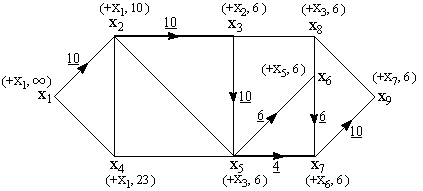
Рис. 23. Потоки и пометки после второй итерации

.

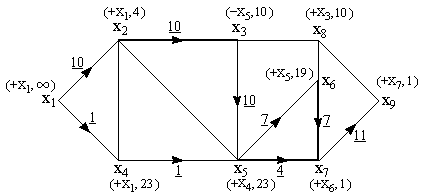
Рис. 24. Потоки и пометки после третьей итерации

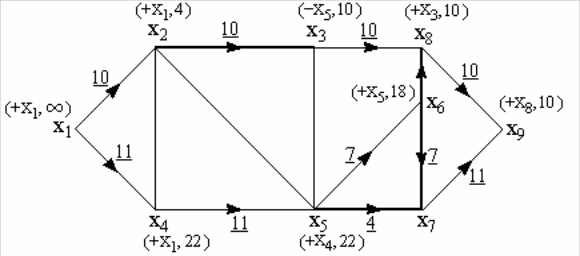
Рис. 25. Потоки и пометки после четвертой итерации

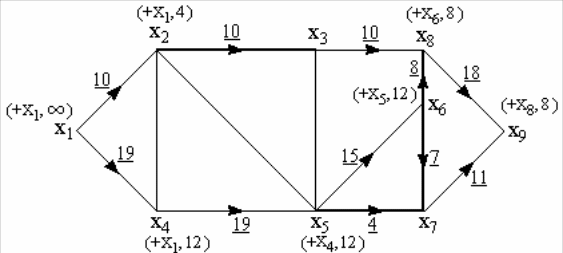
Рис. 26. Потоки и пометки после пятой итерации

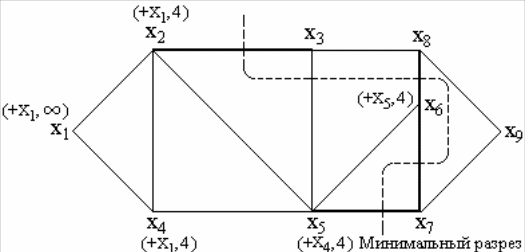
Рис. 27. Потоки и пометки после шестой итерации