
Введение в математический анализ. Учебное пособие. Батаронов И.Л., Провоторова Е.Н
.pdfИ.Л.Батаронов Е.Н.Провоторова Е.Г.Глушко В.В.Дежин
ВВЕДЕНИЕ
В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебное пособие
Воронеж 2002
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
И.Л.Батаронов Е.Н.Провоторова Е.Г.Глушко В.В.Дежин
ВВЕДЕНИЕ
В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебное пособие
Воронеж 2002

УДК 517.9
Введение в математический анализ: Учеб.пособие / И.Л.Батаронов, Е.Н.Провоторова, Е.Г.Глушко, В.В.Дежин. Воронеж: Воронеж. гос. техн. ун-т, 2002. 142 с.
В пособии содержатся основные теоретические сведения по разделу «Введение в математический анализ». В каждой главе даны практические задачи, разбитые на три уровня сложности. Издание соответствует рабочей программе дисциплины «Математический анализ» и предназначено для студентов специальностей 075500 «Информационная безопасность» и 075200 «Компьютерная безопасность» дневной формы обучения.
Учебное пособие подготовлено на оптическом носителе в текстовом редакторе МS Word 97 и содержится в файлах «Начало и окончание.doc», «Глава_1_1.doc», «Глава_1_2.doc», «Глава_2.doc», «Глава_3_1.doc», «Глава_3_2.doc», «Глава_4.doc» и «Глава_5.doc».
Ил. 51. Библиогр.: 14 назв.
Рецензенты: кафедра математического анализа Воронежского государственного университета; канд.физ.-мат.наук, проф. М.Г.Завгородний
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
Батаронов И.Л., Провоторова Е.Н., Глушко Е.Г., Дежин В.В., 2002
Воронежский государственный технический университет, 2002

ВВЕДЕНИЕ
Раздел «Введение в математический анализ» является одним из наиболее важных и сложных при изучении курса математического анализа. Глубокое неформальное понимание таких основных понятий как функция, предел, непрерывность, знание основных теорем о пределах и непрерывных функциях, умение вычислять пределы необходимо для дальнейшего успешного изучения как курса математического анализа так и других математических и специальных дисциплин.
ВI главе пособия содержатся необходимые теоретические сведения по дополнительным главам математического анализа, теории множеств и отображений, рассматриваются понятия бинарных отношений, мощности множеств.
Во II главе вводится понятие предела числовой последовательности, верхнего и нижнего предела, изучаются свойства сходящихся числовых последовательностей, критерии сходимости.
ВIII главе подробно описываются свойства числовых функций, приводятся графики основных элементарных функций, изучаются методы преобразования графиков функций.
IV и V главы посвящены изучению предела и непрерывности функций, свойств непрерывных функций.
Вконце каждой главы приведены задачи для самостоятельного решения. Для удобства организации учебного процесса в группах с различным уровнем математической подготовки задачи приведены в трех уровнях сложности.
Вгруппе «А» содержатся типовые задания облегченного содержания, в группе «Б» более сложные стандартные задачи, в группе «В» предлагаются задачи, требующие глубокого понимания теоретического материала.
Решая задачи из разных групп, студенты могут самостоятельно контролировать уровень усвоения учебного материала.
Пособие может использоваться как студентами для подготовки к практическим занятиям, контрольным работам, экзаменам так и преподавателем при проведении практических занятий, коллоквиумов, экзаменов.
1.ДЕЙСТВИТЕЛЬНАЯ ПРЯМАЯ
1.1. Множества. Операции над множествами
Понятие множества является одним из основных первичных неопределяемых понятий математики. Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку. Будем считать множество заданным, если известен закон, по которому можно сказать принадлежит некоторый объект данному множеству или нет. Объекты, из которых состоит множество, называются его элементами. Множества при-
нято обозначать заглавными буквами алфавита A , B , , а их элементы – малыми a , b , . Если элемент x принадлежит множеству X , то пишут x X , запись x X - означает, что элемент x не принадлежит множе-
ству X .
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом . Элементы множества записываются в фигурных скобках, внутри которых они перечислены, либо указано общее свойство, которым обладают все элементы данного множества.
Например, A |
1, 2, 3 , A |
x : 0 x 2 . |
|
|
|
|
|
||
Множество A называется подмножеством множества B , если каждый элемент множе- |
|||||||||
ства A принадлежит множеству B , обозначается так A |
B . |
|
|
||||||
Множества A и B называются равными, если A |
B и B |
A . |
|
||||||
Объединением A B множеств A и |
B называется множество, |
составленное из тех и |
|||||||
только |
тех |
элементов, |
которые |
принадлежат |
хотя |
бы одному |
из данных множеств: |
||
A B |
x : x |
A или x |
B . |
|
|
|
|
|
|
Пересечением множеств A и B называется множество, составленное из всех тех элемен- |
|||||||||
тов, которые принадлежат как A , так и B : |
A B |
x : x |
A и x |
B . |
|
||||
Совокупность тех элементов из A , которые не содержатся в B , называется разностью |
|||||||||
множеств A и B : A \ B |
x : x |
A и x |
B . |
|
|
|
|
||
Пример. Пусть A |
5, 6, 7,8,9 |
и B |
3, 6, 9 |
. Тогда A B |
3,5, 6, 7,8,9 , A B 6,9 , |
||||
A \ B |
5, 7,8 . |
|
|
|
|
|
|
|
|
Произведением множеств A B называется множество всевозможных пар |
x, y , таких, |
||
что x A, y |
B . |
|
|
Объединением любого (конечного или бесконечного) числа множеств называется множе- |
|||
ство Ai |
x : i : x |
Ai . |
|
Пересечением любого (конечного или бесконечного) числа множеств называется множе- |
|||
ство Ai |
x : i : x |
Ai . |
|
Операции объединения и пересечения обладают свойствами коммутативности, ассо- |
|||
циативности, дистрибутивности, как арифметические операции над числами, |
но A A A , |
||
A A A , A BC  A B
A B A C
A C .
.
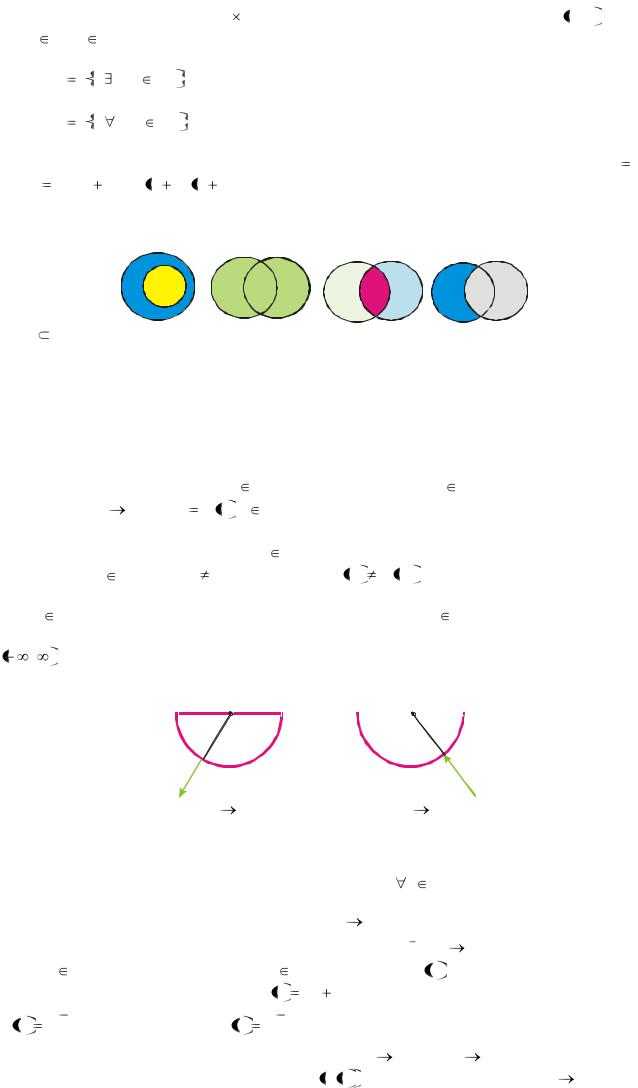
Для наглядного представления операций над множествами используются диаграммы Эй-
лера-Венна (рис. 1).
|
B |
A |
A |
|
B |
A |
|
B |
A |
B |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
B |
A B |
A B |
|
A B |
A \ B |
|
|
|
|||
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
1.2. Отображение множеств |
|
|
|||||
Определение 1. Отображением f |
множества X в множество Y , называется соответст- |
|||||||||
вие, которое каждому элементу x |
X сопоставляет элемент |
y |
Y . Такое отображение обо- |
|||||||
значается f : X |
Y или y |
f x , x |
X . Элемент y |
называется образом элемента x , элемент |
||||||
x - прообразом элемента y при отображении f . |
|
|
|
|
|
|||||
Определение 2. Если каждому x |
X отображение |
f ставит в соответствие единствен- |
||||||||
ный элемент y |
Y |
и при x1 |
x2 выполняется |
f x1 |
f |
x2 , |
то отображение называется вза- |
|||
имно однозначным. Иными словами, отображение является взаимно однозначным, если каж-
дый y |
Y является образом одного и только одного элемента x |
X . |
|||||||||||||||||||
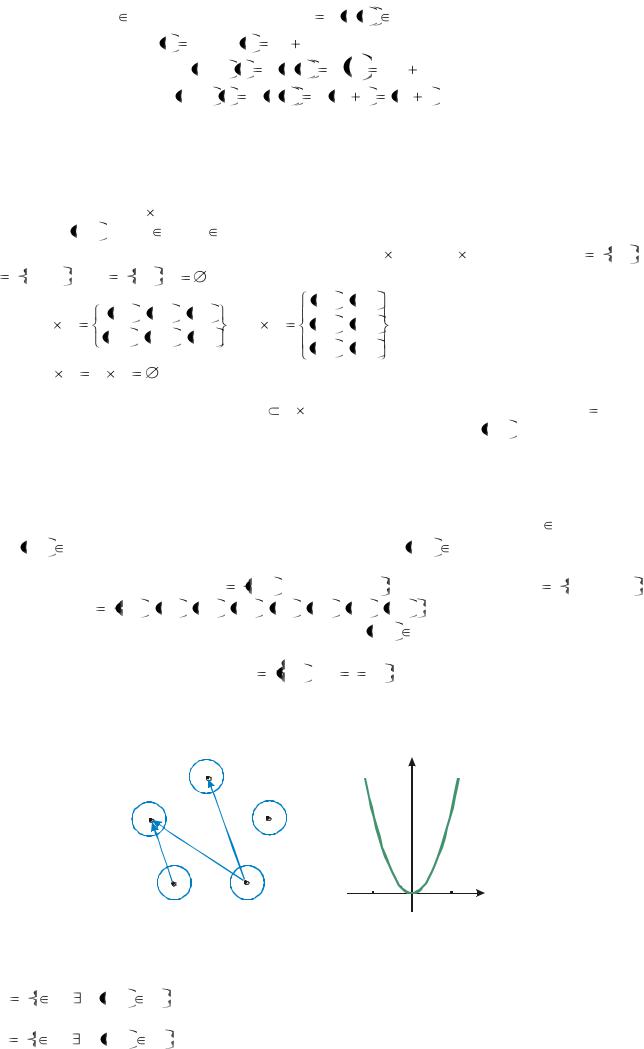
Пример 1. Пусть |
A - полуокружность без крайних точек, |
B - бесконечная прямая |
|||||||||||||||||||
, |
|
. Тогда между |
A и B существует взаимно однозначное соответствие. Закон отобра- |
||||||||||||||||||
жения следует из рис. 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
||
|
|
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
B |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
A B |
|
|
|
|
|
|
|
|
|
B |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
||
Пример 2. Отображение, ставящее в соответствие |
x |
|
R его квадрат, не является вза- |
||||||||||||||||||
имно однозначным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определение 3. Пусть отображение |
f : X |
Y взаимно однозначное. Отображением |
|||||||||||||||||||
обратным к отображению f называется отображение |
f |
1 : Y |
|
X , которое каждому эле- |
|||||||||||||||||
менту y |
Y сопоставляет тот элемент x |
X , для которого |
f |
x |
является образом. |
||||||||||||||||
Пример 3. Для отображения |
f x |
|
|
3x |
2 |
множества |
R в себя обратным является |
||||||||||||||
g y |
y |
2 |
или, что все равно g x |
|
x |
2 |
. |
|
|
|
|
|
|
|
|
|
|||||
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определение 4. Пусть имеем отображения |
f : A |
B и g : B |
C . Суперпозицией g f |
||||||||||||||||||
отображений, или сложным отображением |
g f |
x |
называется отображение A C , состоя- |
||||||||||||||||||
щее в последовательном выполнении сначала отображения f , а потом g , т.е. отображение,
которое каждому x |
A сопоставляет элемент z g f |
x |
C . |
|
|
|
|
|
|
||||||||||||||
|
Пример 4. Пусть |
f |
x |
x2 |
|
и g x |
2x 1. Тогда |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
g f x |
|
g f x |
g x2 |
2x2 |
1. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
f g x |
f g x |
f 2x 1 2x 1 2 . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1.3. Бинарные отношения на множестве |
|
|
|
|
|
||||||||||
|
Отношением называется свойство, которым обладают или не обладают элементы мно- |
||||||||||||||||||||||
жества. Отношение называется бинарным, если оно связывает два элемента. |
|
|
|
||||||||||||||||||||
|
Произведением |
A |
B двух непустых множеств |
A и B называется множество упорядо- |
|||||||||||||||||||
ченных пар |
a, b , где a |
A и b |
|
B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример |
1. |
Перечислим |
|
элементы множеств |
A |
|
B |
и |
B |
A , если |
1) |
A |
1, 2 , |
|||||||||
B |
3, 4, 5 |
; 2) A |
|
1, 2 , B |
|
. Согласно определению получаем: |
|
|
|
|
|||||||||||||
|
|
|
|
1, 3 , |
1, 4 , |
1, 5 |
|
|
|
3, 1 , 3, 2 |
|
|
|
|
|
|
|
|
|
||||
|
1) A B |
|
, |
B A 4, 1 , 4, 2 ; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2, 3 , |
2, 4 , |
2, 5 |
|
|
5, 1 , 5, 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2) A |
B |
B |
A |
|
, поскольку множество B пусто и мы не можем составить ни одной |
|||||||||||||||||
пары. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 1. Любое подмножество |
R |
A |
B называется бинарным отношением. Если |
A |
B , то |
|||||||||||||||||
бинарное отношение называется бинарным отношением на множестве |
A . Если пара a, b принадлежит бинар- |
||||||||||||||||||||||
ному отношению R , то говорят, что a находится в отношении R к b и пишут a Rb . |
|
|
|
||||||||||||||||||||
|
Для задания бинарного отношения R используют те же методы, |
что и для произвольных множеств, кроме |
|||||||||||||||||||||
того, бинарное отношение, заданное на конечном множестве A , можно задать в виде графа, а бинарное отноше- |
|||||||||||||||||||||||
ние на множестве R можно задать в виде декартовой диаграммы. Под графом бинарного отношения понимают |
|||||||||||||||||||||||
схему, в которой элементы множества |
|
A изображаются точками на плоскости, |
элементы a, b |
R , такие, что |
|||||||||||||||||||
пары |
a, b |
R соединяются стрелкой, направленной от a к b , пары a, a |
R изображаются петлей вокруг |
||||||||||||||||||||
точки a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Бинарное отношение R |
a, b : a делится на b , заданное на множестве A |
2, 3, 5, 6, 8 |
||||||||||||||||||||
будет иметь вид R |
2, 2 , |
3,3 , 5,5 , 6,6 , |
8,8 , |
6, 2 , 6,3 , |
8, 2 |
|
(рис. 3). |
|
|
|
|||||||||||||
|
Под декартовой диаграммой понимают изображение пар |
a, b |
|
|
R в декартовой прямоугольной систе- |
||||||||||||||||||
ме координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. Для бинарного отношения R |
x, y : x2 |
y , определенного на множестве R , декарто- |
||||||||||||||||||||
ва диаграмма будет следующей (рис. 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
|
|
|
6 |
5 |
|
|
|
4 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
0 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
Рис. 4 |
|
|
|
|
|
|||||
|
Областью |
определения |
|
бинарного |
отношения |
R |
|
называется |
множество |
||||||||||||||
DR |
a A : b a, b R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Областью |
значений |
|
бинарного |
отношения |
|
|
|
R |
|
называется |
множество |
|||||||||||
ER |
b B : |
a a, b R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Свойства бинарных отношений:

1. Бинарное отношение R на множестве A называется рефлексивным, если для a A пара a, a R . Если A - конечное множество, то рефлексивность бинарного отношения R означает, что на графе данного бинарного отношения вокруг каждой точки a A есть петля. Ес-
R . Если A - конечное множество, то рефлексивность бинарного отношения R означает, что на графе данного бинарного отношения вокруг каждой точки a A есть петля. Ес-
ли A |
R , то рефлексивность бинарного отношения с точки зрения декартовой диаграммы оз- |
начает, что в число изображенных точек войдут все точки прямой y x x . |
|
|
2. Бинарное отношение R на множестве A называется антирефлексивным, если для |
a |
A пара a, a R . Если A - конечное множество, то антирефлексивность бинарного от- |
ношения R означает, что на графе данного бинарного отношения вокруг каждой точки a A отсутствует петля. Если A R , то антирефлексивность бинарного отношения с точки зрения декартовой диаграммы означает, что в число изображенных точек не войдет ни одна точка прямой y x x .
3. |
Бинарное отношение R на множестве A называется симметричным, если для |
|
a,b |
A из принадлежности пары a, b отношению R следует принадлежность этому от- |
|
ношению также пары |
b, a . Если A - конечное множество, то симметричность бинарного от- |
|
ношения R означает, |
что на графе данного бинарного отношения все присутствующие стрел- |
|
ки двусторонние. Если A R , то симметричность бинарного отношения с точки зрения декартовой диаграммы означает, что изображенное множество симметрично относительно пря-
мой y x x . |
|
4. Бинарное отношение R на множестве |
A называется антисимметричным, если для |
a,b A из принадлежности пар a, b и b, a |
отношению R следует a b . Если A - ко- |
нечное множество, то антисимметричность бинарного отношения R означает, что на графе |
|
данного бинарного отношения все присутствующие стрелки односторонние. Если A R , то |
|
антисимметричность бинарного отношения с точки зрения декартовой диаграммы означает, что изображенное множество расположено по одну сторону от прямой y x x .
5. |
Бинарное отношение R |
на множестве |
A |
называется |
транзитивным, |
если |
для |
|||
a,b, c |
A из принадлежности пар |
a, b |
и |
b, |
c |
отношению |
R следует принадлежность |
|||
этому отношению также пары a, |
c . |
|
|
|
|
|
|
|
|
|
6. Бинарное отношение R на множестве A называется связанным, если для |
a,b |
A из |
||||||||
a b следует принадлежность a, b |
или |
b, a |
отношению R . Если A - конечное множество, |
|||||||
то связанность бинарного отношения R означает, |
что на графе данного бинарного отношения |
|||||||||
все элементы множества связаны односторонними или двусторонними стрелками.
Пример 4. Для каждого из следующих бинарных отношений выяснить, какими свойст-
вами оно обладает и какими не обладает. |
|
|||
1) |
R |
1, 2 , 2,1 , |
1,1 , 1,3 , 3, 2 , 3,3 на X 1, 2,3 ; |
|
2) |
R |
x, y : x y |
Z на множестве X |
R ; |
3) |
R |
x, y : 2x |
3y на множестве X |
Z ; |
Решение. |
|
|
|
|
|
|
|
|
|
1) Данное отношение |
|
|
|
|
|
|
|
|
|
- не является рефлексивным, так как для элемента 2 |
X пара 2, 2 |
R ; |
|
||||||
- не является антирефлексивным, так как имеются пары |
1,1 |
и |
3, 3 |
, принадлежащие R ; |
|||||
- не является симметричным, так как 1,3 |
R , а |
3,1 |
R ; |
|
|
|
|
||
- не является антисимметричным, так как пары 1, 2 и |
2,1 принадлежат R , но 1 |
2 ; |
|||||||
- не является транзитивным, так как пары |
3, 2 |
и |
2,1 |
принадлежат R , а 3,1 R ; |
|
||||
- является связанным, так как пары 1, 2 , |
2,1 , |
1, 3 |
и |
3,1 |
принадлежат R , т.е. все различ- |
||||
ные элементы связаны. |
|
|
|
|
|
|
|
|
|
2) Данное отношение |
|
|
|
|
|
|
|
|
|
- является рефлексивным, поскольку для |
x |
X разность x |
x |
0 |
Z , т.е. x, x |
R ; |
|||
- не является антирефлексивным, так как оно является рефлексивным, т.е. содержит все точки прямой y x ;
- является симметричным, поскольку принадлежность любой пары x, y отношению R означает x y k Z , но тогда и y x
отношению R означает x y k Z , но тогда и y x 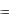 k Z , т.е. y, x
k Z , т.е. y, x R ;
R ;

- не является антисимметричным, так как, например, пары |
4.5, 2.5 и |
2.5, 4.5 |
принадлежат |
|||||||||||||||||||
R , но 4.5 |
2.5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- является транзитивным, поскольку для |
x, y, z |
|
R принадлежность |
x, y |
и |
y, z |
отноше- |
|||||||||||||||
нию R означает x |
y |
k |
Z и y |
z |
n |
Z , но тогда x |
z |
k n Z , т.е. |
x, |
z |
R ; |
|
||||||||||
- не является связанным, так как, например, для |
x |
1 |
y |
1,5 |
получим |
x |
y |
0,5 |
Z и |
|||||||||||||
y x |
0,5 |
Z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) Данное отношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
- не является рефлексивным, так как из всех пар |
x, x , x |
Z только пара |
0, 0 |
|
R , а для ос- |
|||||||||||||||||
тальных x |
Z не выполняется равенство 2x |
3x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- не является антирефлексивным, так как пара |
0, 0 |
|
R ; |
|
|
|
|
|
|
|
|
|
|
|||||||||
- не является симметричным, так как |
3, 2 |
R |
2 3 |
3 2 , а |
2,3 |
R |
2 2 |
|
3 3 ; |
|
|
|||||||||||
- является антисимметричным, поскольку для любых пар |
|
x, y |
R и |
y, |
x |
|
R |
должны вы- |
||||||||||||||
полняться равенства 2x |
|
3y и 2y |
|
3x , т.е. |
4x |
9x |
и 9y |
4y , но это может быть только в |
||||||||||||||
том случае, если x |
y |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
- не является транзитивным, так как, например, |
пара 9, 6 |
R |
2 9 |
3 6 |
и пара |
6, 4 |
R |
|||||||||||||||
2 6 |
3 4 , но пара |
9, 4 |
R 2 9 |
|
3 4 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- не является связанным, так как, например, для x |
|
1 |
y |
4 получим 2 1 |
3 4 и 2 4 |
3 1. |
||||||||||||||||
|
Отношение нестрогого порядка x |
y обладает свойствами |
|
|
|
|
|
|
|
|
|
|
||||||||||
-антисимметричности;
-рефлексивности;
-транзитивности.
Отношение строгого порядка x y обладает свойствами
-антисимметричности;
-антирефлексивности;
-транзитивности.
Пример 5.
1)Отношения строгого порядка на множествах N , R и C являются связанными.
2) Для любого множества M отношение XRY |
X |
Y , где X ,Y |
M , является отношением строго- |
|||||||||||
го порядка, но не обладает свойством связанности. |
|
|
|
|
|
|
|
|||||||
3) На множестве всюду определенных функций отношение нестрогого порядка |
|
|
|
|||||||||||
fRg |
x |
R : |
f x |
g |
x не обладает свойством связанности. |
|
|
|
|
|||||
4) Отношение ARB |
A старше чем B на множестве людей Земли является строгим, но не связан- |
|||||||||||||
ным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 2. Рефлексивное, симметричное и транзитивное отношение R на множестве |
X называется |
|||||||||||||
отношением эквивалентности на множестве |
X . |
Для отношения эквивалентности часто используют запись |
||||||||||||
x y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение 3. Классом эквивалентности, порожденным элементом |
x , называется подмножество мно- |
|||||||||||||
жества X , состоящее из тех элементов y X , для которых |
x, y R . |
|
|
|
|
|||||||||
Пример 5. Пусть |
n некоторое натуральное число. Проверить, является ли отношением эквивалентности |
|||||||||||||
следующее бинарное отношение на множестве целых чисел |
|
|
|
|
|
|||||||||
|
|
|
|
|
R |
x, y |
Z |
Z : x y делится на n . |
|
|
|
|||
Решение. Проверим три основных свойства для отношения эквивалентности. |
|
|
|
|||||||||||
1) Рефлексивность: для |
x |
Z выполняется x |
x |
0 |
|
|
|
|
||||||
0 n |
x, x |
R . |
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
Симметричность: |
|
|
пусть |
x, y R |
k |
Z x |
y |
|||
k n |
|
k Z y x |
k n |
y, x R . |
|
|
|
|
|
|
||||
3) |
|
|
|
Транзитивность: |
|
|
|
пусть |
x, y |
R, |
y, z |
R |
||
k, m Z x y k n, y z m n |
k, m Z x z |
|
|
|
|
|||||||||
k m n |
|
r k m Z x z r n |
|
x, z R . |
|
|
|
|
||||||
Итак, исследуемое бинарное отношение является отношением эквивалентности.
Определение 4. Обратным отношением для R называется отношение R 1 |
x, y : y, x |
R . |
|||||||
Определение |
5. |
Композицией |
отношений |
R1 |
и |
R2 |
называется |
отношение |
|
R2 R1 |
x, y : z x, z R1, z, y R2 . |
|
|
|
|
|
|||
Для любых бинарных отношений выполняются следующие свойства:

1. R 1  1 R ;
1 R ;
|
2. R |
2 |
R |
1 |
R |
1 R 1 . |
|
|
|
|
1 |
1 |
2 |
|
|
||
|
Пример 6. Пусть на множестве R заданы следующие бинарные отношения: |
|||||||
R |
x, y : x y2 |
, R |
x, y :x y 2 |
, R |
x, y : x y Z . |
|||
1 |
|
|
|
|
2 |
|
3 |
|
Найти обратные к данным бинарным отношениям и композиции отношений.
Решение.
R 1 |
x, y : y, x R |
x, y : y x2 ; |
|
1 |
1 |
|
|
R 1 |
x, y : y, x R |
x, y : y x 2 R |
; |
2 |
2 |
2 |
|
R 1 |
x, y : y, x R |
x, y : y x Z R . |
|
3 |
|
3 |
3 |
R1 R2 |
x, y : z x, z R2, z, y R1 |
||
x, y : z x z 2, z y2 |
x, y : x y2 2 ; |
||
R2 R3 |
x, y : z x, z R3, z, y R2 |
||
x, y : z x z Z, z y 2 x, y : z x z k Z, z y 2
x, y : k Z k x y 2 R R .
Остальные композиции постройте самостоятельно.
1.4. Счетные множества. Понятие мощности множеств
Для характеристики степени насыщенности бесконечных множеств элементами используются понятия эквивалентности и мощности множеств.
Определение 1. Два множества называются эквивалентными или равномощными, если между их элементами можно установить взаимно однозначное соответствие.
Определение 2. Если множество X эквивалентно множеству натуральных чисел N , то множество X называется счетным, т.е. все элементы множества можно перенумеровать с помощью натуральных чисел и запи-
сать в виде последовательности элементов: X |
x1, x2 , , |
xn , . |
|
|
||||
Пример 1. Множество N натуральных чисел и множество Z целых чисел эквивалентны. Взаимно одно- |
||||||||
значное соответствие устанавливается следующим образом |
|
|
|
|
||||
, |
3, |
2, |
1, |
0, |
1, |
2, |
3, |
|
|
|
|
|
|
|
|
|
|
, |
7, |
5, |
3, |
1, |
2, |
4, |
6, |
|
Отсюда следует, что множество Z счетно. |
|
|
|
|
|
|
|
|||||
Пример 2. |
Отрезки |
0, 1 и |
a, b эквивалентны. Соответствие устанавливается с помощью отображения |
|||||||||
|
|
|
X |
b |
a x |
a, 0 |
x |
1. |
||||
Пример 3. |
Интервал |
0, 1 |
эквивалентен R . Соответствие устанавливается с помощью отображения |
|||||||||
|
|
|
X |
1 |
|
arctg |
1 |
|
|
, |
x |
R . |
|
|
|
|
|
x |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|||
Отметим наиболее важные свойства счетных множеств.
1.Каждое бесконечное подмножество счетного множества счетно.
2.Объединение конечной или счетной совокупности счетных множеств счетно.
3.Каждое бесконечное множество содержит счетное подмножество.
Теорема 1. Множество Q рациональных чисел счетно.
Интересно доказательство этой теоремы. Расположим все рациональные числа в таблицу, содержащую бесконечное число строк и столбцов. Здесь в n -ю строчку помещены рациональные числа, записываемые несократимыми рациональными дробями со знаменателем n и упорядоченные по возрастанию их абсолютных величин, причем непосредственно за каждым положительным числом следует ему противоположное. Очевидно, что каждое рациональное число находится на каком-то месте в этой таблице.

0 |
1 |
1 |
2 |
2 |
3 |
|
|||||||
1 |
1 |
3 |
|
3 |
5 |
|
5 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
|
2 |
2 |
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|||||
1 |
1 |
|
|
|
|
|
|||||||
|
|
|
|||||||||||
n |
|
n |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
Занумеруем теперь элементы получившейся таблицы согласно следующей схеме, в которой в кружочках стоят номера соответствующих элементов, а стрелки указывают направление нумерации:
1 |
2 |
4 |
7 |
11 |
3 |
5 |
8 |
12 |
|
6 |
9 |
13 |
|
|
10 |
14 |
|
|
|
15 |
|
|
|
|
В результате все рациональные числа оказываются занумерованными, т.е. множество Q счетно. Следствие 1. Множество всех многочленов с рациональными коэффициентами a0 , a1, , an счетно.
Следствие 2. Множество всех алгебраических чисел (т.е. корней многочленов с рациональными коэффициентами) счетно.
Бесконечные множества не являющиеся счетными называются несчетными множествами. Теорема 2 (Кантор). Множество всех точек отрезка 0, 1 несчетно.
Из этой теоремы и примера 3 следует, что множества всех действительных чисел R , а, следовательно, и всех комплексных чисел C несчетны.
Заметим, что, так как множество рациональных чисел отрезка 0, 1 счетно, следовательно, иррациональ-
ных чисел «значительно больше» чем рациональных. Более того, так как иррациональные алгебраические числа составляют счетное множество, то несчетное множество составляют числа, не являющиеся корнями многочленов с рациональными коэффициентами – трансцендентные числа.
Эквивалентные между собой два конечных множества состоят из одинакового числа элементов, т.е. конечные множества можно сравнивать по числу элементов. Но как сравнивать бесконечные множества? Если произ-
вольные множества A и B эквивалентны, то говорят, что множества A и B имеют одинаковую мощность, таким образом, мощность – это то общее, что есть у всех эквивалентных между собой множеств. Мощность мно-
жества A обозначается A . Мощность счетного множества обозначается א0 (алеф-нуль). Множества эквива-
лентные отрезку 0, 1 называются множествами мощности континуум. Мощность континуум обозначается бук-
называются множествами мощности континуум. Мощность континуум обозначается бук-
вой C .
Примеры 1 и 3 показывают, что часть множества может быть эквивалентна всему множеству. Это свойство характерно для всех бесконечных множеств. Пусть множества A и B неэквивалентны, но в A есть под-
множество эквивалентное B , тогда говорят, что мощность A больше мощности B : A
 B .
B .
Из свойства 3 следует, что из всех бесконечных множеств счетные множества имеют наименьшую мощность, а из теоремы Кантора и свойства 3 следует, что C>א0.
При сравнении бесконечных множеств используются следующие две наиболее важнейшие теоремы – тео-
рема Кантора-Бернштейна и теорема 4. |
|
Теорема 3 (Кантора-Бернштейна). Пусть A и |
B - два произвольных множества. Если в A имеется |
подмножество A1 B , а в B имеется подмножество |
B1 A , то множества A и B эквивалентны между со- |
бой. |
|
Теорема 4. Множество всех подмножеств множества M имеет мощность большую, чем мощность множества M .
