
Кратные интегралы. Векторный анализ. Учебное пособие по решению задач и выполнению типовых расчетов. Катрахова А.А., Купцов В.С
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
А.А. Катрахова В.С. Купцов
КРАТНЫЕ ИНТЕГРАЛЫ. ВЕКТОРНЫЙ АНАЛИЗ
Учебное пособие по решению задач и выполнению
типовых расчетов
Воронеж 2002

УДК 517.53
Катрахова А.А. Кратные интегралы. Векторный анализ: Учеб. пособие /А.А. Катрахова, В.С. Купцов. Воронеж: ВГТУ, 2002. 101 с.
Учебное пособие является руководством к решению практических задач и выполнению типовых расчетов по разделам «Кратные интегралы. Векторный анализ» в соответствии с программой курса «Математики» для студентов инженернотехнических специальностей вузов. Оно содержит подробные решения задач и краткое изложение теоретического материала по указанным разделам.
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD 97.0 и содержится в файле
«Integral1. rar.» и в файле «Integral2. rar.»
Табл. 1. Ил. 38. Библиогр.: 8 назв.
Научный редактор д-р физ.-мат. наук А.В. Глушак
Рецензенты: кафедра дифференциальных уравнений ВГУ; д-р физ.-мат. наук, проф. А.Г. Баскаков
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
Катрахова А.А., Купцов В.С., 2002
2

Оформление. Воронежский государственный технический университет, 2002
ВВЕДЕНИЕ
Настоящее учебное пособие содержит разбор и подробное решение типовых задач по разделам кратные, криволинейные и поверхностные интегралы и векторный анализ. Содержание пособия соответствует программе курса математики для студентов инженерно-технических специальностей вузов рассчитанной на 600 часов и утвержденной Министерством образования Российской Федерации в соответствии с новыми образовательными стандартами.
Каждому практическому занятию предпосылается конспективное изложение основных сведений из теории, справочные данные и формулы, относящиеся к соответствующему разделу. После подробного разбора типовых задач различной степени трудности помещены задачи для самостоятельного решения, которые в нужных случаях снабжены указаниями и ответами. Некоторые задачи решены различными способами. Такое построение пособия предоставляет студентам широкие возможности для активного самостоятельного изучения практической части курса математики.
1.ДВОЙНОЙ ИНТЕГРАЛ
1.1.Вычисление двойного интеграла в декартовых прямоугольниках. Изменение порядка интегрирования
а) Двойной интеграл по прямоугольной области
Если область D, на которую распространяется двойной интеграл
3
f ( x, y )ds |
f ( x, y )dxdy |
(1.1) |
D |
D |
|
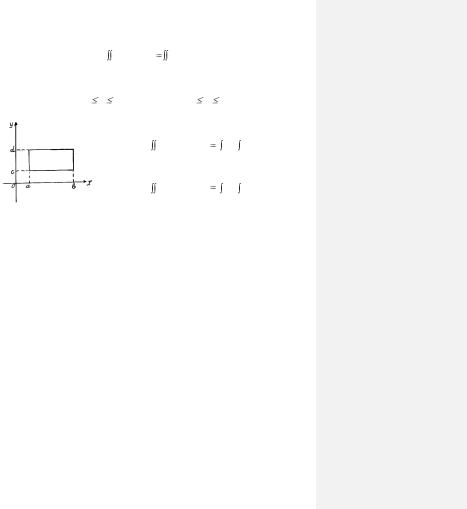
прямоугольник со сторонами, параллельными координатным осям и определяемыми уравнениями
х = а, х = b, (а х b), у = с, у = d, (с у d), то двойной интеграл вычисляется по одной из формул:
|
d |
|
b |
|
|
f ( x, y )dxdy |
dy |
f ( x, y )dx |
(1.2) |
D |
c |
|
a |
|
|
или |
|
|
|
|
b |
|
d |
|
|
f ( x, y )dxdy |
dy |
f ( x, y )dy |
(1.3) |
D |
a |
|
c |
|
Рис. 1.1
Интегралы, стоящие в правых частях этих формул называются повторными или двухкратными.
b
В формуле (1.2)  f ( x, y )dx называется внутренним и вы- a
f ( x, y )dx называется внутренним и вы- a
числяется в предположении, что переменная у сохраняет на отрезке [a, b] фиксированное постоянное значение. При этом подынтегральная функция f(х, у) является функцией только одной переменной х. В результате вычисления этого интеграла получится функция переменной у.
После того, как эта функция определена, надо выполнить внешнее интегрирование под переменной у. В результате этого вторичного интегрирования получится уже не функция, а число.
Если же для вычисления двойного интеграла применяется формула (1.3), то порядок интегрирования меняется. Первое (внутреннее) интегрирование ведется по переменной у в предположении, что переменная а на отрезке [c, d] сохраняет постоянное фиксированное значение, а повторное (внешнее) интегри-
4
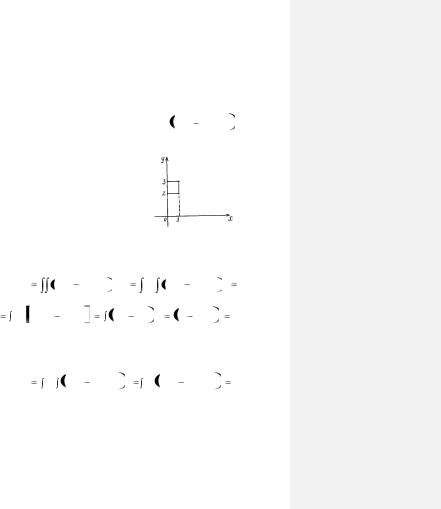
рование по переменной х. В результате вычисления внутреннего
d
интеграла 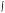 f ( x, y )dy получится функция переменной х, а по- c
f ( x, y )dy получится функция переменной х, а по- c
вторное интегрирование дает число.
Задача 1.1.
Вычислить двойной интеграл 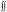 6 xy2 12x2 y dxdy по об-
6 xy2 12x2 y dxdy по об-
D
ласти D, ограниченной: х = 0; х = 1; у = 2; у = 3.
Решение. Область D
представляет собой квадрат со сторонами, параллельными координатным осям (рис. 1.2). Произведем вычисление этого интеграла сначала по формуле
(1.2).
Рис.1.2
Получим:
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
I |
|
|
|
6xy2 |
|
12x2 y dxdy |
|
dy 6xy2 |
12x2 y dx |
|
||||||||
|
|
|
D |
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
3 |
|
2 |
|
2 |
|
3 |
|
1 |
3 |
|
2 |
|
|
3 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dy 3x |
y |
4x |
y |
|
3 y |
4 y dy y |
2 y |
|
9 . |
|||||||||
|
|
|
|
0 |
|
|
|
|
|
2 |
|||||||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
Изменим порядок интегрирования, т.е. и вычислим внутренний интеграл по у, а внешний по х, по формуле (1.3).
Получим:
1 |
3 |
2 |
|
2 |
|
1 |
3 |
|
2 |
|
2 |
3 |
|
I |
dx 6 xy |
12x |
y dy |
dx 2xy |
6 x |
y |
|||||||
|
|
|
|
|
2 |
||||||||
0 |
2 |
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
5 |
|
|
|
|
|
|

1 |
|
54x2 |
16 x 24x2 |
1 |
2 dx |
||
54x |
dx 38x 30x |
||||||
0 |
|
|
|
|
|
0 |
|
19x |
2 |
10x |
3 |
|
9 . |
|
|
1 |
|
|
|||||
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
Ответ: I = 9.
Поскольку подынтегральная функция непрерывна, то результаты вычислений совпали, они не зависят от порядка интегрирования.
б) Двойной интеграл по произвольной плоской фигуре
Если область интегрирования D ограничена кривой, которую каждая прямая, параллельная оси ОУ, пересекает не более чем в двух точках рис. 1.3, то двойной интеграл, распространенный на эту область, вычисляется по формуле:
|
b |
2 ( x ) |
|
f ( x, y )dxdy |
dx |
f ( x, y )dxdy |
(1.4) |
D |
a |
1 ( x ) |
|
1(х) и 2(х) на отрезке [a, b] непрерывны, обозначены и сохраняют аналитическое выражение.
Интеграл в правой части этой формулы также называется повторным или двухкратным.
Если область D ограничена кривой, которую любая прямая, параллельная оси ОХ, пересекает не более, чем в двух точках (рис. 1.4), то двойной интеграл, распространенный
на эту область, может быть вычислен по формуле:
6
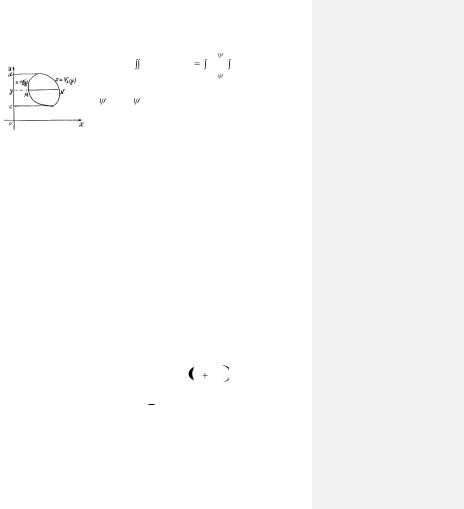
|
d |
2 ( y ) |
f ( x, y )dxdy |
dy |
f ( x, y )dx . (1.5) |
D |
c |
1 ( y ) |
Причем предполагается, что функции 1(у) и 2(у) на отрезке [c, d] однозначны, непрерывны и сохраняют аналитическое выра-
жение.
Рис. 1.4
Следует обратить внимание на то, что во внешнем интеграле в обоих случаях пределы интегрирования величины постоянные и в результате вычисления двойного интеграла получится постоянная величина.
Если подынтегральная функция f(x, y) непрерывна в области D, то значение повторного интеграла, распространенного на эту область, не зависит от порядка интегрирования по различным аргументам.
Свойства определенных интегралов распространяются и на двойные интегралы. В формулах (1.4) и (1.5) для вычисления двойного интеграла предполагалось, кривая, ограничивающая область интегрирования D, пересекается всякой прямой, параллельной одной из координатных осей, не больше, чем в двух точках. Если это условие не выполнено, то область D следует разбить на части так, чтобы в каждой из частей это условие выполнялось.
Задача 1.2.
Вычислить двойной интеграл 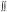 x3 y3 dxdy, если область
x3 y3 dxdy, если область
D
D ограничена линиями у = 21 х, у = х, х = 4. Вычислить этот же интервал, изменив порядок интегрирования.
7

Решение. Представим на чертеже область D (рис. 1.5). Воспользуемся формулой (1.4).
Получим:
|
x3 |
y3 |
4 |
x |
I |
dxdy |
dx x3 y3 |
||
|
D |
|
0 |
x |
|
|
2 |
||
|
|
|
|
Чтобы получить пределы интег-
рирования в повторном интеграле спроектируем область D на ось ОХ, получим отрезок [0, 4], таким образом, нижний предел изменяется переменной х равен 0, а верхний 4 во внешнем интеграле. Затем на отрезке [0, 4] оси ОХ выбирается произвольная точка Х, через которую проводится прямая, параллельная оси
ОУ.
Область D ограничена силу прямой у = 21 х, а сверху –
прямой у = х (Уравнения линий, ограничивающих область D, должны быть разрешены относительно той переменной, по которой вычисляется внутренний интеграл).
Вычисление следует начинать с внутреннего интеграла:
x |
|
|
|
|
|
|
|
y |
4 |
|
|
x |
||
x3 |
y3 |
dy |
x3 |
y |
|
|
|
|
|
|
|
|||
4 |
|
1 |
x |
|||||||||||
x |
|
|
|
|
|
|
|
2 |
||||||
2 |
1 |
|
|
1 |
|
1 |
|
|
|
|
|
47 |
|
|
x3 x |
x |
x4 |
x4 |
|
|
|
x4 . |
|||||||
2 |
4 |
16 |
|
64 |
||||||||||
|
|
|
|
|
|
|
||||||||
Получилась функция переменной х. Вычислим теперь интеграл:
4 |
47 |
x4 dx |
47 |
|
x |
5 |
|
4 |
|
752 |
. |
|
|
|
|
|
|
||||||
0 |
64 |
64 |
5 |
|
0 |
5 |
|||||
|
|
|
|||||||||
8
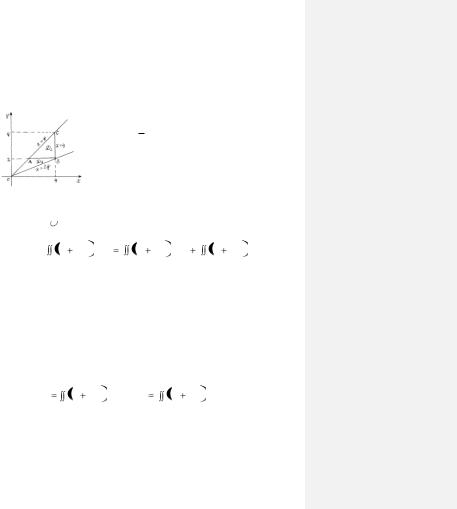
Вычислим теперь тот же интеграл, измерив порядок интегрирования: внутреннее интегрирование произведем по переменной х, а внешнее – по у.
Из чертежа (рис. 1.6) видно, что левая часть контура области D одна линия х = у, а правая состоит из двух линий, определяемых разными уравнениями: уравнение
ОВ у = 21 х, а уравнение ВС х = 4. В этом
случае область D следует разбить на части так, чтобы из них справа ограничивалась линией, определяемой одним аналитическим выражением. Такими частями будут области D1, ограниченная контуром ОАВ и область D2, ограниченная контуром АСВ. Область
D = D1 D2. По этому по свойству аддитивности двойного интеграла, получим
x3 y3 dxdy |
x3 y3 dxdy |
x3 y3 dxdy. |
D |
D1 |
D2 |
Так как теперь внутренние интегралы будут вычисляться по переменной х, то уравнения линий, ограничивающих каждую из областей D1 и D2 должны быть решены относительно переменной х.
Область D1 ограничена прямыми х = у, х = 2у, у = 2. Область D2 ограничена прямыми х = у, х = 4, у = 2. Точка В имеет координаты (4; 2). Спроектировав каждую
из областей интегрирования D1 и D2 на ось ОУ получим пределы интегрирования внешних интегралов: в первом интеграле от 0 до 2, во втором от 2 до 4. Обозначим:
I1 |
x3 y3 dxdy, I2 |
x3 y3 dxdy. |
|
D |
D2 |
Получим:
9

2 |
2 y |
|
2 |
x |
4 |
|
2 y |
|
|
|
|
||||||
I1 |
dy x3 |
y3 |
dx dy |
|
y3 x |
|
||
4 |
y |
|||||||
0 |
y |
|
0 |
|
||||
2 |
|
1 |
|
16 y |
4 |
|
y |
4 |
|
y |
3 |
2 y y dy |
2 |
19 |
y |
4 |
dy |
|
19 |
y |
5 |
2 |
152 |
. |
|||||||||||||||
0 |
4 |
|
|
|
|
|
|
0 |
4 |
|
20 |
|
0 |
5 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
4 |
|
|
x |
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
I2 |
|
|
dy x3 |
|
|
y3 dx dy |
|
|
|
|
|
y3 x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
4 |
|
|
|
y |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
y |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
1 |
|
4 |
4 |
|
y |
4 |
|
|
y |
3 |
4 y dy |
4 |
64 4 y |
3 |
|
5 |
y |
4 |
dy |
|
|
||||||||||||||||
2 |
4 |
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
64 y |
|
y4 |
|
1 |
y5 |
|
|
120 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Искомый интеграл равен сумме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
I1 |
|
I2 |
|
|
152 |
120 |
752 |
150 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Ответ: |
I 150 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты вычислений совпали, поскольку подынтегральная функция х3 + у3 непрерывна в области D, но выбрав рационально порядок интегрирования можно сократить вычисления. В данной задаче более рационально в повторном интеграле производить внутреннее интегрирование по у, а внешнее по х.
Задачи для самостоятельного решения
Задача 1.4. Вычислить двойной интеграл x y dxdy.
D
10
