Учебное пособие 1868

Задача 4.10. Вычислить интеграл

J = xdydz+2ydxdz+zdxdy, где Σ – положительная сторона ку-

ба, составленного плоскостями x=0 , y=0, z=0, x=2, y=2, z=2.

Ответ: 8.

Задача 4.11. Вычислить координаты центра тяжести однородного полушара x2 + y2+ z2 = 4, z = 0 (z ≥ 0).

Ответ: (0, 0, 1,5).

Задача 4.12. Вычислить массу тела, ограниченного по-

верхностями на 2x + z = 2, x+ z = 1, y2 = x, y = 0 (y > 0), если плотность его в каждой точке равна y этой точки.

Ответ: 1/(12).

5. ТЕОРИЯ ПОЛЯ

Понятие поля лежит в основе многих представлений современной физики. Изложим элементы того математического аппарата, которым приходится пользоваться при изучении физических полей.

В физических задачах чаще всего встречаются величины двух типов: скаляры и векторы. В соответствии с этим мы будем рассматривать два типа полей – скалярные и векторные.

5.1. Скалярные поля

Пусть Ω - некоторая область в пространстве. В этой области задано скалярное поле, если каждой точке М этой области поставлено в соответствие некоторое число U (М).

Примерами скалярных полей служат: поле температур внутри некоторого нагретого тела (в каждой точке М этого тела задана соответствующая температура U (М)); поле освещенно-

81

сти, создаваемое каким-либо источником света; поле плотности массы и т.д.

Пусть U(М) – некоторое скалярное поле, то, введя в области, где задано поле, декартовы координаты, можно представить это поле в виде непрерывной функции U(x, у, z) и имеющей в рассматриваемой области непрерывные частные производные первого порядка по х, у и z. Задание скалярного поля с помощью фиксированной системы координат и функции U (х, у, z) не всегда дает достаточно ясное представление о поведении этого поля. Для получения наглядной картины удобно пользоваться называемыми поверхностями уровня. Поверхностью уровня скалярного поля U (M) называется геометрическое место точек, в которых поле U(М) имеет данное фиксированное значение С. Уравнение поверхности уровня имеет вид U(x, у, z) = С. Задание всех поверхностей уровня с отметкой на них соответствующих значений С равносильно заданию поля U(М). Взаимное расположение поверхностей уровня в пространстве дает наглядное представление о соответствующем скалярном поле.

Этот способ изображения поля удобен тогда, когда поле, задано не в пространственной, а в плоской области. Такое поле описывается функцией двух переменных U(x, у). Равенство вида U(x, у) = С определяет некоторую кривую. Такие кривые называются линиями уровня плоского скалярного поля U (М). Во многих физических задачах приходится иметь дело с полями, обладающими свойствами симметрии, облегчающими изучение таких полей.

Частные случаи: Плоскопараллельное поле. Если скалярное поле U (М) в декартовой системе координат можно описать функцией, зависящей от двух координат (U(x, у)), то поле называется плоскопараллельным (двумерным). Поле U (M) называется плоскопараллельным, если в пространстве существует направление, при сдвигах вдоль которого поле U (M) переходит

82

само в себя. Поверхности уровня такого поля – это семейство (U(x, y) = C) цилиндрических поверхностей (рис. 4.2).

Осесимметрическое поле. Если для поля U (M) можно подобрать такую цилиндрическую систему координат, в которой

оно изображается функцией, зависящей только от переменных r = (х2+ у2)1/2 и z (но не от угла υ), то это поле называется осе-

симметрическим. Поверхности уровня такого поля представляют собой поверхности вращения. Если эти поверхности вращения – круглые цилиндры, т.е. если поле U (М) в соответствующей цилиндрической системе координат изображается функцией, зависящей лишь от одной координаты r (расстояния точки от оси симметрии поля), то U (М) называется цилиндрическим полем.

Сферическое поле. Если значения U (М) зависят лишь от расстояния точки М от некоторой фиксированной точки М0,то такое поле называется сферическим. Поверхности уровня сферичеcкого поля будут являтся семейством концентрических сфер .

Задача 5.1. Найти область определения функции

z =1 /(x2 + y2) и определить линии уровня скалярного поля z.

Решение.

Поле z определено во всем пространстве за исключением точек, для которых x2+y2=0, т.е. x = 0, y = 0.

Линии уровня определяются уравнением 1/(x2+y2) = C, C (x2 + y2) = 1 – уравнения семейства окружностей.

Производная по направлению

При изучении скалярного поля методами анализа мы должны описать его локальные свойства, т.е. изменение вели-

83

чины U (М) при переходе от данной точки М к близким точкам. Для этого будем использовать производную поля по направлению.

Пусть U (М) – скалярное поле. Рассмотрим две близкие точки М, М* и отношение (U(M*) – U(M))/h (где h – длина отрезка ММ*), и пусть точка М* приближается к М, причем направление отрезка ММ* совпадает с направлением фиксирован-

ного единичного вектора . Если при этом вышеуказанное отношение стремится к некоторому пределу, то этот предел называется производной скалярного поля U (М) в точке М по на-

правлению 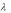и обозначается ∂U(M)/∂λ. Эта производная харак-

теризует скорость изменения величины U(M) в направлении . Для ее вычисления выберем некоторую систему координат и представим U(М) в виде U(x, у, z).

Пусть направление образует с осями координат углы

α,β,γ. Тогда ММ* = h (icos α+ jcos β + kcosγ) и U (М*)= U (х+ hcosa, y+hcosβ, z+hcosγ), а производная ∂U/∂λ- совпадает с производной по h от сложной функции U(M*) при h = 0. Дифференцируя, получаем

cosγ), определяющего направление, по которому берется производная и вектора, имеющего координаты ∂U/∂x, ∂U/∂y, ∂U/∂z.

кривую, касательная к которой в каждой ее точке направлена по grad U в этой же точке. Линии градиента поля – это те линии, вдоль которых поле U меняется быстрее всего. Если функция U(x, у, z) имеет непрерывные частные производные до второго порядка включительно, то через каждую точку области, в которой задано поле U, проходит одна и только одна линия градиента. В каждой точке линия градиента ортогональна той поверхности уровня, на которой эта точка лежит.

Задача 5.2. Найти производную скалярного поля

Решение. Вычислим

grad U=(∂U/∂x, ∂U/∂y, ∂U/∂z) = (y+z2y3, x+2z2y2, x+2zy3x), grad U М =(2,3,3). ∂U/∂I М = (grad U М ,I)= 2+3+3=7.

5.2. Векторные поля

85

B некоторой области Ω определено векторное поле, если каждой точке М этой области поставлен в соответствие опреде-

ленный вектор A (М).

Если A (М) – некоторое векторное поле в пространстве, то, взяв в этом пространстве какую-либо декартову систему ко-

ординат, мы можем представить A (М) как совокупность трех скалярных функций – компонент этого вектора. Эти компоненты мы будем обозначать Р(х, у, z), Q(x, у, z) и R(x, у, z). Далее мы будем рассматривать векторные поля, компоненты которых непрерывны и имеют непрерывные частные производные первого порядка.

Пусть в области Ω задано векторное поле A (M). Кривая L, лежащая в Ω, называется векторной линией, если в каждой точке этой кривой направление касательной к ней совпадает с на-

правлением вектора A в этой же точке.

В вопросах, связанных с изучением полей, важную роль

играет задача о нахождении векторной линии поля r , проходящей через данную точку М0. Эта задача формулируется так:

требуется найти вектор-функцию r (t), для которой выполнено

r '(t) = λ A , r (t0) = r 0, где r - радиус-вектор начальной точки М0, t0-начальный момент времени, а λ- произвольная числовая величина. Ограниченная некоторой поверхностью Σ часть про-

странства, в котором задано векторное поле A , называется векторной трубкой, если в каждой точке поверхности Σ нормаль к

поверхности Σ ортогональна вектору A в этой же точке. Изучение векторного поля (как и скалярного) существенно облегчается, если это поле обладает свойствами симметрии.

Рассмотрим частные случаи векторных полей: Плоскопа-

раллельное поле. Если для данного векторного поля A можно подобрать декартову систему координат, в которой компоненты

поля A имеют вид Р(х, у), Q(x, у), R(x, у) (т.е. не зависят от z), то

86

поле A называется плоскопараллельным. Если при этом R(x, у)

= 0, то поле A называется плоским. Векторные линии такого поля – плоские кривые (одни и те же в каждой параллельной

Осесимметрическое поле. Векторное поле будет называется осесимметрическим, если существует такая цилиндрическая система координат r, υ, z, что в каждой точке М вектор

A (M) зависит лишь от r и z, но не от υ. Иными словами, такое поле переходит само в себя при повороте вокруг оси z. Если

вектор A (М) зависит только от r, то поле называется цилиндрическим.

Одномерное поле. Векторное поле называется одномерным, если существует такая декартова система координат, в которой компоненты этого поля имеют вид Р(х), 0, 0. Векторные линии такого поля представляют собой, очевидно, совокупность всех прямых, параллельных оси х.

Рассмотрим снова некоторое скалярное поле U(М). Построив в каждой точке М вектор grad U, мы получим векторное поле – поле градиента скалярной величины U. Введем следую-

щее: Векторное поле A (М) называется потенциальным, если его можно представить как градиент некоторого скалярного по-

ля U (М): A = grad U. Само скалярное поле U называется при

этом потенциалом векторного поля A .

Если векторное поле A имеет потенциал, то этот потенци-

ал определяется полем A однозначно, с точностью до произвольного постоянного слагаемого. Векторные линии потенци-

ального поля A представляют собой, разумеется, линии гради-

87

гралу Аn dσ, где An – нормальная составляющая вектора

скорости A = ( Р, Q, R). Величина П называется потоком жид-

кости через поверхность Σ. Пусть A произвольное векторное поле и Σ ориентированная поверхность. Поверхностный интеграл

мы назовем потоком векторного поля A через поверхность.

Пусть A - некоторое векторное поле. Поставим в соответствие каждой пространственной области Ω, ограниченной гладкой или кусочно-гладкой поверхностью Σ, величину

и назовем ее потоком вектора А через внешнюю сторону поверхности Σ. Мы получим аддитивную функцию области Ф(Ω). Производная функции Ф (Ω) по объему, т.е. предел (5.4) назы-

вается дивергенцией векторного поля A и обозначается div A .

Если A = (P, Q, R) – векторное поле, определенное в области Ω и такое, что функции Р, Q, R непрерывны в Ω вместе со всеми

своими первыми производными, то div A существует во всех точках этой области (в любой декартовой системе координат) и выражается формулой

Замечание. Равенство ∂Р/∂x + ∂Q/∂y + ∂R/∂z = div A

принимают за определение дивергенции, но это определение менее удобно, так как оно опирается на выбор той или иной системы координат, и необходимо доказывать, что сумма ∂P/∂x + ∂Q/∂y + ∂R/∂z от выбора системы координат не зависит, а независимость от выбора системы координат выражения (5.5) очевидна.

89

Каждому векторному полю A , компоненты которого непрерывны и имеют непрерывные частные производные, можно

поставить в соответствие скалярную функцию div A . Пользуясь этим понятием, формулу Остроградского можно записать так

т.е. поток вектора A через внешнюю сторону замкнутой по-

верхности Σ равен интегралу от дивергенции поля A , взятому по области, ограниченной поверхностью Σ.

Соленоидальное поле

Векторное поле, дивергенция которого тождественно равна нулю, называется соленоидальным или трубчатым. Для соленоидальных полей выполнен закон сохранения интенсивности векторной трубки.

ний) и возьмем ее отрезок, заключенный между двумя ее сечениями Σ1 и Σ2 (рис. 5.1).

Эти сечения вместе с боковой поверхностью Σ трубки образуют замкнутую поверхность Σ3. Так как поле соленоидально, т.е.

div А ≡ 0, в силу формулы Остроградского

Рис. 5.1

90