
Учебное пособие 1868
.pdf
Область D ограничена линиями х = 0, y |
3 |
x( x 0 ), у |
|
2 |
|||
= 4 – (х – 1)2. |
|
||
|
|
Этот же интеграл вычислить, изменив порядок интегрирования.
Указание. При вычислении внутреннего интеграла по у, а внешнего по х (см. рис. 1.7) получим
2 |
4 ( x |
1 )2 |
208 |
|
|
I |
dx |
x y dy |
. |
||
15 |
|||||
0 |
3 |
|
|
||
2 x |
|
|
|
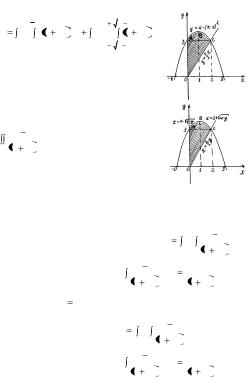
При вычислении внутреннего интеграла по х, а внешнего по у область надо разбить на две части ОАС и АВС (см. рис. 1.7)
и разрешить уравнение параболы |
у = 4 – (х – 1)2 относительно |
||||||||
|
|
|
|
|
|
|
|
|
|
переменной х, получим |
x |
1 |
|
4 y , |
причем линия АВ опре- |
||||
|
|
|
|
|
|
|
|
|
|
деляется |
уравнением x |
1 |
4 |
y , а |
линия ВС уравнением |
||||
|
|
|
|
|
|
|
|
|
|
x 1 |
4 y . |
|
|
|
|
|
|
|
|
11
|
|
После |
изменения порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
интегрирования получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
32 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
1 |
4 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I |
dy |
x |
y |
dx |
dy |
x y |
dx |
|
|
|
|
|
|
|
|
|
||||||||||
0 |
0 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
4 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
208 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Задача |
|
|
1.6. |
|
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
двойной |
|
|
|
|
|
|
|
интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
y |
dxdy |
по |
области D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
D x |
y 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ограниченной прямыми: |
х = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
х = 1, у = 0, у = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Показать, |
что |
изменение |
|
|
|
|
|
|
|
Рис. 1.7 |
|
|
||||||||||||
порядка интегрирования приво- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
дит к различным результатам и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
объяснить причину этого. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
x |
|
y |
|
|
|
|
|
Указание. а) С одной стороны |
|
|
I |
dx |
|
|
|
dy . |
|
|||||||||||||||
|
|
|
|
x |
|
y 3 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|||
|
|
Внутренний интеграл |
1 |
|
x |
y |
|
|
dy |
|
|
|
1 |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
0 |
|
x |
y 3 |
|
1 |
x 2 |
|
|
||||||||||||||||
|
|
Ответ: |
|
I |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
x y |
|
|
|
|
|
|
|
|
|||
|
|
б) С другой стороны |
I |
|
dy |
|
|
|
|
|
|
dx . |
|
|
|
|
||||||||||
|
|
|
|
x |
y 3 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|||||
|
|
Внутренний интеграл |
1 |
|
x |
y |
|
|
dx |
|
|
|
1 |
|
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
x |
y 3 |
|
1 |
y 2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Ответ: I  21 .
21 .
Различные результаты вычислений объясняются тем, что в точке (0, 0) подынтегральная функция не является непрерывной.
|
Задача 1.7. Вычислить двойной интеграл |
|
|
|
|
|||||||||||
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
по области, |
ограниченной линиями |
х = 0, |
у |
|||||||||
D x2 |
y2 2 |
|||||||||||||||
= 0, х = 1, у = 1 и объяснить, |
почему ответ зависит от порядка |
|||||||||||||||
интегрирования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ответ: а) I |
|
|
; б) I |
|
|
|
. |
|
|
|
|
|
|
||
|
|
4 |
|
4 |
|
|
|
|
|
|
||||||
|
1.2. Вычисление двойного интеграла в полярных коор- |
|||||||||||||||
динатах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
В полярных координатах dS = rdrd |
, x = rcos , |
y = rsin , |
|||||||||||||
где r – полярный радиус (0 |
|
r + |
), |
– полярный угол (0 |
||||||||||||
2 |
), а двойной интеграл: |
|
|
|
|
|
|
|||||||||
|
|
|
f |
x, y dS |
f |
|
r cos |
, r sin |
rdrd . |
(1.6) |
||||||
|
|
|
D |
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
Область D должна быть отнесена к полярной системе ко- |
|||||||||||||||
|
|
|
|
|
ординат (рис. 1.8). |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Если |
|
|
она ограничена |
двумя лучами |
||||||
|
|
|
|
|
с уравнениями |
|
= |
и |
= |
( |
) и |
|||||
|
|
|
|
|
линиями, определяемыми уравнениями r = |
|||||||||||
|
|
|
|
|
u1( ) и |
|
|
|
r = u2( |
), где функции u1( |
) и |
|||||
|
|
|
|
|
u2( ) непрерывна на отрезке [ , |
], одно- |
||||||||||
|
Рис. 1.8 |
|
значны и |
сохраняют аналитическое выра- |
||||||||||||
|
|
жение, то двойной интеграл, распростра- |
||||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
ненный на эту область, вычисляется |
по |
||||||||||
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
||

формуле (1.6):
|
u2 ( |
) |
|
F( r, )rdrd |
d |
F( r, )rdr . |
(1.6) |
D |
u1 ( |
) |
|
Интеграл, стоящий в правой части этой формулы – повторный (иначе двукратный). Во внутреннем интеграле следует рассматривать как величину постоянную.
Задача 1.8. Вычислить 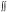 r 2 sin drd , где область D ог-
r 2 sin drd , где область D ог-
D
раничена линиями r = R и r = 2R sin .
Решение. Область D ограничена окружностями радиуса R, одна из них с центром в начале координат (r = R), а другая с центром в точке с координата-
ми (O, R) на оси ОУ (рис. 1.9). Чтобы определить, как изменяется в области D полярный угол , проведем лучи из начала координат в точки А и В. Решая систему уравнений
r R
, найдем значения
r 2R sin
угла , соответствующие лучам ОА и ОВ.
Получим 2R sin |
= R; sin = |
1 |
, |
|
|
, |
|
5 |
. |
|||
|
1 |
|
2 |
|
||||||||
|
|
|
|
2 |
|
6 |
|
6 |
|
|||
|
|
|
|
|
|
|
|
|
||||
Таким образом, |
пределы изменения полярного угла в |
|||||||||||
области D от |
|
до |
5 |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
6 |
6 |
|
|
|
|
|
|
|
|
|
||
Теперь найдем пределы изменения полярного радиуса в |
||||||||||||
области D. Для этого под произвольным углу |
|
, взятым в про- |
||||||||||
|
|
|
|
14 |
|
|
|
|
|
|
|
|
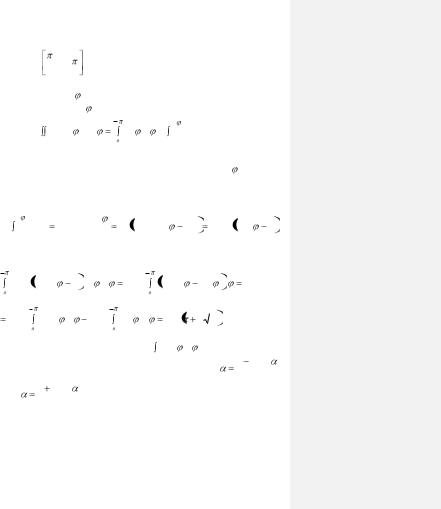
межутке |
|
, |
5 |
проведем из полюса О луч ОР. В точке С |
|
|
|||
6 |
|
6 |
|
|
входа этого луча в область D r = R, а в точке Р выхода из области r = 2R sin , поэтому полярный радиус изменяется в об-
ласти D R до 2R sin .
|
5 |
|
2R sin |
|
Поэтому r 2 sin drd |
6 |
|
||
|
|
sin d |
r 2 dr . |
|
D |
|
|
|
R |
6 |
|
|||
|
|
|
||
(Мы вынесли sin за знак внутреннего интеграла, так как при вычислении внутреннего интеграла переменная сохраняет постоянное значение).
за знак внутреннего интеграла, так как при вычислении внутреннего интеграла переменная сохраняет постоянное значение).
Внутренний интеграл равен
2R sin |
r |
3 |
|
2R sin |
1 |
|
|
1 |
|
|
|
r 2dr |
|
|
|
8R3 sin3 |
R3 |
R3 |
sin3 |
1 |
|||
|
|
|
R |
|
|
||||||
R |
3 |
|
3 |
|
3 |
|
|
|
|||
Внешний интеграл равен
5 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
||||
6 |
R |
3 |
|
8 sin |
3 |
1 sin |
d |
|
R |
3 6 |
|
8 sin |
4 |
sin |
d |
|
|||||||||||||||||
|
3 |
|
|
|
3 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
5 |
|
|
|
|
|
1 |
|
|
5 |
|
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
|||
|
|
|
3 |
6 |
|
|
4 |
|
|
|
3 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
R |
|
sin |
d |
R |
sin |
|
d |
|
|
|
3 3 . |
|
|
|||||||||||||||||||
|
3 |
|
|
|
|
|
3 |
|
|
|
|
12 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Указание. При вычислении |
|
sin4 d |
следует использо- |
|||||||||||||||||||||||||
вать |
|
|
|
тригонометрические |
|
формулы |
sin2 |
|
1 cos 2 |
; |
|||||||||||||||||||||||
|
|
|
|
2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos2 |
|
1 |
cos 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
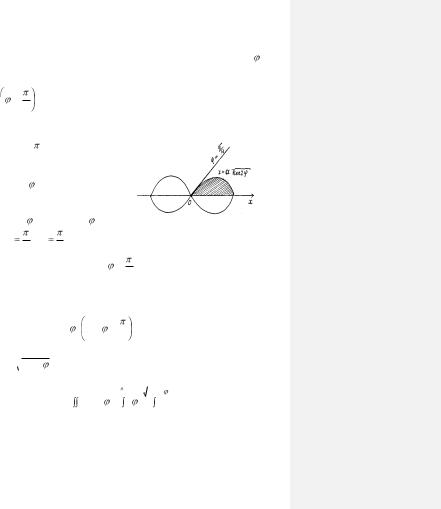
Задача 1.9. Вычислить двойной интеграл  r3drd , где
r3drd , где
D
область D ограничена полярной осью и кривой r2 = a2cos2
 2 .
2 .
Решение. Кривая r2 = a2cos2 – лемниската. В области D полярный угол изменяется
– лемниската. В области D полярный угол изменяется
от 0 до |
|
. |
|
|
|
|
4 |
|
|
|
|
||
Верхний предел изме- |
|
|||||
нения |
можно получать из |
|
||||
уравнения лемнискаты, под- |
|
|||||
ставив |
|
r |
= |
0, то |
есть |
|
a2cos2 |
= |
0; |
cos2 |
= 0, |
Рис. 1.10 |
|
|
|
|
|
|
|
|
2 2 ,
2 ,  4 .
4 .
(Учтено условие 2 ). Нижний предел получается из
условия, что область D ограничена полярной осью. Чтобы определить пределы изменения полярного радиуса области D, проведем луч из полюса О, пересекающий область D под произ-
вольным углом |
0 |
|
|
. Он входит в область D в полюсе, |
4 |
то есть при r = 0, а выходит в точке на лемнискате, в котором r = a 
 cos 2 .
cos 2 .
|
|
|
|
а |
cos2 |
|
Получим: r3drd |
4 |
|
||||
|
|
|
r 3dr . |
|||
= d |
|
|
||||
D |
0 |
|
|
0 |
|
|
Внутренний интеграл равен
16
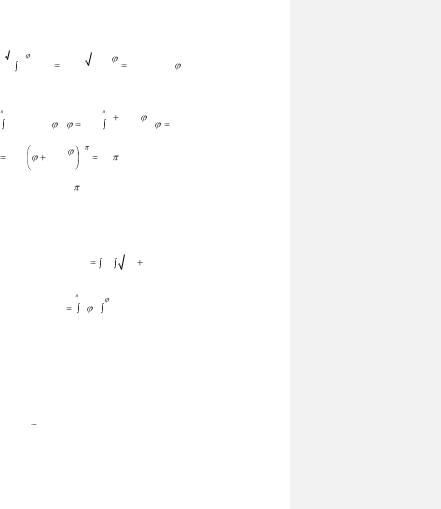
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a cos 2 |
3 |
|
|
|
24 |
|
|
a |
|
cos 2 |
|
|
|
1 |
|
4 |
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
r |
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
cos |
|
2 . |
|||
|
|
|
0 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
4 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Внешний интеграл равен |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
1 |
|
cos 4 |
|
|
|
|
|
|||||||||
|
4 |
1 |
a |
4 |
cos |
2 |
2 |
d |
a |
|
4 |
|
|
d |
|
|
||||||||||||||||||||
0 4 |
|
|
|
|
4 |
0 |
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
4 |
|
|
|
|
|
sin4 |
|
|
|
|
|
|
1 |
a |
4 |
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
8 a |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
a4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Задачи для самостоятельного решения |
|||||||||||||||||||||||||||||||
|
|
|
|
|
Задача 1.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
y2 dy |
|
||||||||
|
|
|
|
|
В интеграле |
|
|
|
I |
|
|
|
|
dx x |
|
перейти к полярным ко- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
||
ординатам. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sec |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Ответ: |
I |
|
d |
|
|
|
|
|
r 2dr . |
|
|
|
|
|
|
||||||||||||||||
00
1.3.Применение двойных интегралов для вычисления площадей и объемов
а) Вычисление площадей плоских фигур
Площадь плоской фигуры вычисляется по формуле:
S  dS ,
dS ,
D
где dS дифференциал площади.
17
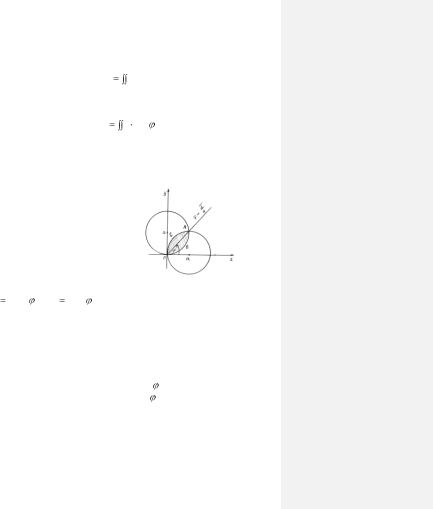
Если фигура отнесена к прямоугольной системе координат, то предыдущая формула примет вид:
|
|
S |
dxdy . |
(1.7) |
|
|
|
D |
|
Если фигура отнесена к полярной системе координат, то ее |
||||
площадь вычисляется по формуле: |
|
|||
|
|
S |
r drd . |
(1.8) |
|
|
|
D |
|
Задача 1.11. Найти площадь фигуры, ограниченной ли- |
||||
ниями (х – а)2 + у2 = а2 |
и х2 + (у – а)2 = а2. |
|||
Решение. |
|
|
|
|
Линии, |
ограничивающие |
|
||
область, это окружности с цен- |
|
|||
трами в точках (а, 0) и (0, а) ра- |
|
|||
диуса а. |
|
|
|
|
Наличие в уравнении кри- |
|
|||
вой выражения х2 + у2 указывает |
|
|||
на целесообразность перехода к |
|
|||
полярным координатам по фор- |
|
|||
мулам: |
|
|
|
Рис. 1.11 |
x r cos , y |
r sin , |
х2 + у2 |
||
= r2.
Если раскрыть скобки, то уравнения окружностей запи-
шутся в виде:
х2 + у2 – 2ах = 0; х2 + у2 – 2ау = 0.
В полярных координатах они примут вид: |
|
r = 2 acos |
(1.9) |
r = 2 asin |
(1.10) |
Луч ОА делит искомую площадь на две части D1 и D2 (рис. 1.11). Решая совместно уравнения (1.9) и (1.10) получим, что
18
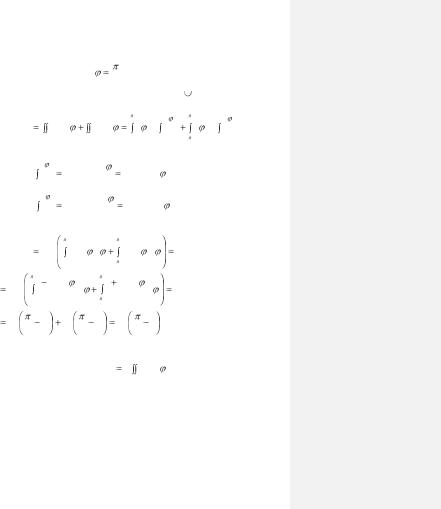
точка А лежит на биссектрисе первого координатного угла.
Уравнение луча ОА: |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|||||||||||||||||||||||
|
Искомая площадь области D = D1 |
D2 |
в силу свойства |
|||||||||||||||||||||||||||||
аддитивности двойного интеграла равна: |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 a sin |
|
|
2 a cos |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
||||||||
|
S |
|
|
rdrd |
|
|
|
|
rdrd |
|
|
|
|
|
|
d |
rdr |
d |
rdr . |
|||||||||||||
|
|
|
|
|
D1 |
|
|
|
|
|
|
D2 |
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||||||||||||
|
Вычислим отдельно внутренние интегралы: |
|||||||||||||||||||||||||||||||
|
2 a sin |
|
|
r |
2 |
|
2 a sin |
|
|
|
2 a2 sin2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
rdr |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 a cos |
|
|
r |
2 |
|
2 a cos |
|
|
|
2 a2 cos2 . |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
rdr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Поэтому искомая площадь равна: |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a2 |
4 |
sin2 |
|
|
|
|
2 |
|
cos2 |
|
|
|
|
|
|||||||||||||
|
|
S |
|
|
|
d |
|
|
|
d |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 cos 2 |
|
|
|
|
|
|
|
|
|
cos 2 |
|
|
|
|
|
||||||||||||
2a |
2 4 |
|
d |
|
|
2 |
1 |
|
d |
|
|
|
|
|||||||||||||||||||
0 |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a2 |
|
|
|
|
1 |
|
a2 |
|
|
|
1 |
|
|
a2 |
|
|
1 кв. ед. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
4 |
|
2 |
|
|
|
|
|
|
4 |
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||||
Замечание. Так как из рис. (1.11) видно, что искомая площадь области D состоит из двух равных между собой по площади областей D1 и D2, то S 2 rdr d .
D1
Задачи для самостоятельного решения
19

Задача 1.12. Найти площадь, ограниченную линиями х2
+ у2 – 2ах = 0 и х2 + у2 – ах = 0.
Указание. Уравнение линий преобразовать к полярным координатам. Получим
|
|
|
|
|
2 a cos |
|
|
2 |
|
||
|
|
S 2 d |
rdr . |
||
|
|
0 |
|
a cos |
|
Ответ: S |
3 |
a2 кв. ед. |
|
||
4 |
|
||||
|
|
|
|
|
|
Задача 1.13. Найти площадь, ограниченную линиями: х2
+ у2 = R2, х2 + у2 – 2Ry = 0 и х = 0.
Указание. Перейти к полярным координатам, получим
|
|
|
|
|
|
|
|
|
|
2 R sin |
|
|
|
|
|
|
2 |
|
|
||
|
|
|
S |
2 |
|
|
d |
rdr . |
||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
6 |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Ответ: S |
1 |
R2 |
|
|
|
3 |
|
кв. ед. |
||
|
|
|
|
|
|
|
|
|||
|
2 |
3 |
|
|
2 |
|
|
|||
б) Вычисление объемов тел |
||||||||||
Двойной интеграл |
f |
x, y dxdy равен объему цилиндри- |
||||||||
D
ческого тела, ограниченного с боков цилиндрической поверхностью, образующие которой парал-
лельны оси OZ. Направляющей служит контур z, ограничивающий область интегрирования D, лежащую в плоскости ХОУ и являющуюся нижним основанием этого цилиндрического тела. Сверху тело ограничено поверхностью, определяемой уравнением z = f(x, y)
20 Рис. 1.12
