
Учебное пособие 1692
.pdf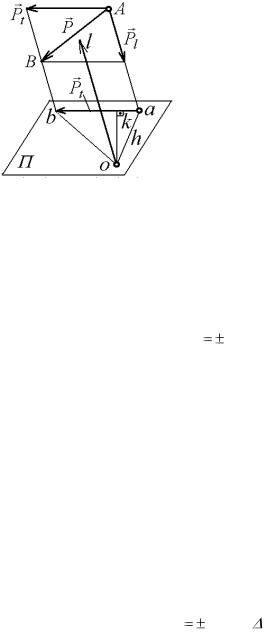
|
|
|
|
|
|
Пусть сила |
P |
приложена в точке А. Разложим силу P |
на |
||
|
|
лежащие в одной плоскости |
со- |
||
|
|
|
|
|
|
|
|
ставляющие, одна из которых - |
Pl |
||
|
|
|
|
|
|
|
|
параллельна оси, а вторая- Pt пер- |
|||
|
|
пендикулярна этой оси (рис. 7.16). |
|||
|
|
|
Пусть П плоскость, перпен- |
||
|
|
дикулярная оси l . Составляющая |
|||
|
|
|
|
|
|
|
|
Pt силы P , параллельная плоско- |
|||
|
|
сти |
П называется составляющей |
||
|
|
силы |
|
вдоль плоскости П. |
|
|
|
P |
|
||
Величиной момента силы |
|
относительно оси l назы- |
|||
P |
|||||
вают алгебраическое значение произведения составляющей силы вдоль плоскости П, перпендикулярной к этой оси, на расстояние от этой проекции до оси, то есть на длину перпендикуляра, опущенного из точки пересечения оси с плоскостью на линию действия этой составляющей (рис. 7.16):
|
|
Ml ( P ) Pt h . |
(7.23) |
Рис. 7.16 |
При определении величины момента си- |
|
лы относительно оси учитывается, что враща- |
||
|
тельное действие силы относительно оси определяется не всей
силой, а только ее составляющей Pt вдоль плоскости, перпен-
дикулярной оси. Другая составляющая Pl , параллельная оси l,
не вызывает вращения, а стремится сдвинуть тело вдоль оси. Величина момента считается положительной, если, смотря
противоположно положительному направлению оси, можно
видеть вращение тела вокруг оси под действием силы P (или
составляющей Pt ) против хода часовой стрелки. При враще-
нии по ходу часовой стрелки величина момента считается отрицательной. Из формулы (7.23) и рис. 7.16 следует
|
Oab , |
(7.24) |
Ml ( P ) 2 пл |
||
126 |
|
|
|
|
т. е. величина момента силы P относительно оси l |
численно |
равна алгебраическому значению удвоенной площади тре- |
|
|
|
угольника, основанием которого служит проекция Pt |
силы P |
на плоскость, перпендикулярную к оси, а вершиной - точка |
|
|
|
пересечения оси с плоскостью. Если сила P параллельна оси, |
|
то Pt = 0, а если ее линия действия пересекает ось, то h = 0. В
обоих случаях, согласно (7.23), M l ( P ) = 0, т. е. величина мо-
мент силы относительно оси равна нулю, когда сила параллельна оси или пересекает эту ось. В обоих случаях сила и ось расположены в одной плоскости.
7.5.6. Теорема 7.2, о связи между величинами моментов силы относительно точки оси и относительно оси
Величина момента силы относительно оси равна проекции на эту ось вектора момента силы,
взятого относительно произвольной точки на данной оси.
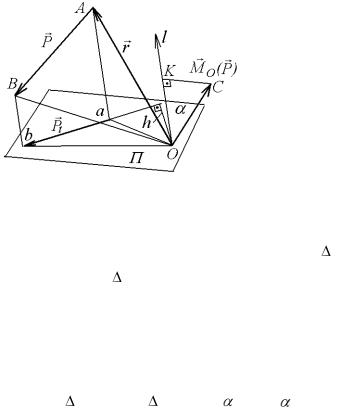
Доказательство. На рис. 7.17 даны построение, необходимое для доказательства теоремы. Согласно (7.17), (7.18) и
рис. 7.17 |
|
|
перпендикулярен плоскости AOB и модуль |
|
M o ( P ) |
||||
|
|
|
|
|
| Mo ( P )| = 2 пл. AOB.
Плоскость П перпендикулярна оси l. Треугольник Оаb есть проекция на плоскость П треугольника OAB. Из геометрии известно, что площадь проекции плоской фигуры равна произведению площади проецируемой фигуры на косинус угла между плоскостью проекции и плоскостью проецируемой фигуры: пл. Оаb = пл. ОAB cos . Угол между плоскостями измеряется соответствующим двугранным углом, равным углу
127

между перпендикулярами к этим плоскостям, проведенными в любой точке пересечения плоскостей (на рис. 7.17 точка О). Учитывая (7.18) и (7.24), получаем
|
|
|
|
|
|
Ml( P ) = 2 пл. Оаb = 2 пл. |
OAB cos |
= |
|||
|
|
|
|
|
|
=| M o ( P ) | cos |
= OK = npl M o ( P ) , |
|
|||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
Ml ( P ) |
npl Mo ( P ) . |
|
(7.25) |
|
Если вместо точки О будет другая точка пересечения плоскости с осью, например точка О1 то площадь  OAB и угол изменяются, а площадь проекции останется прежней (пл. Оаb = пл. O1a1b1 ). Тогда, согласно (7.24), не изменится момент и силы относительно оси. Теорема доказана.
OAB и угол изменяются, а площадь проекции останется прежней (пл. Оаb = пл. O1a1b1 ). Тогда, согласно (7.24), не изменится момент и силы относительно оси. Теорема доказана.
Если центр моментов (точку О) взять в плоскости пары,
|
|
то оба вектора момента M O ( P ) и |
M O ( P ) будут расположе- |
ны на одной прямой, а в этом случае их векторное суммирование моментов можно заменить алгебраическим. Следовательно, имеем частный случай доказанной теоремы: сумма моментов двух сил, составляющих пару, относительно произвольной точки в плоскости пары равна моменту пары
|
|
|
|
M( P ) + M ( P ) = m( P,P ) . |
(7.26) |
||
Формула (7.26) отличается от (7.22) тем, что в нее входят величины моментов, тогда как в (7.22) входят векторы моментов.
7.5.7. Теорема 7.3 о проекции сил пары
Сумма проекций двух сил, составляющих пару, на какую либо ось равна нулю. Правильность этой теоремы очевидна, так как две силы пары параллельны, противоположно направлены и равны по модулю, а поэтому абсолютные величины их
128
проекций одинаковы, но противоположны по знаку.
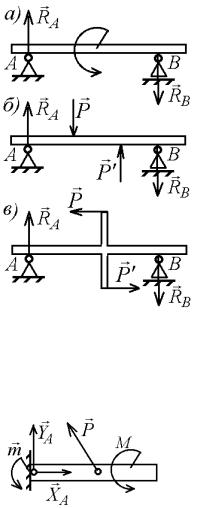
Часто пару изображают в виде изогнутой стрелки с обозначением момента (рис. 7.18, а). Такое упрощенное изобра-
жение оправдано тем, что действие пары характеризуется ее моментом, и при определении опорных реакций, т. е. неизвестных внешних сил следует брать суммы моментов всех сил относительно какойлибо точки, а где приложены силы, составляющие пару на основании (7.26) значения не имеет. Но, если надо определить не внешние силы, а внутренние в разных сечениях балки, как это делается в сопротивлении материалов, то важно знать, где приложены силы пары. Например, внутренние силы для балок, изображенных на рис. 7.17, б и
7.17, в будут различными.
Рис. 7.18 |
Если силы пары приложе- |
|
ны, как показано на рис. 7.18, в, |
||
|
||
то пара и ее момент условно называют сосредоточенными. |
||
Заделка - одна из часто встречающихся связей (опор). Пусть балка (рис. 7.19) имеет один свободный конец, а другой конец жестко заделан в стену. Такая балка называется
Рис. 7.19 одноопорной (консольной). Воздействие стены на балку состоит из ре-
активной сосредоточенной силы RA и реактивной пары сил, момент которой m А называют реактивным моментом, или мо-
129
ментом в заделке. Реактивный момент в заделке вызван парой реакций и препятствует повороту балки, обеспечивая жесткость ее соединения со стеной. При решении задач, выгодно
|
|
|
|
|
|
|
|
|
|
изображать силу RA |
в виде горизонтальной и вертикальной |
||||||||
|
|
|
|
|
|
|
|
|
|
составляющих сил: |
R |
A |
X |
A |
Y |
A |
, из которых X |
A |
направлены |
|
|
|
|
|
|||||
вдоль оси балки, а YA |
- перпендикулярно этой оси. Поэтому |
||||||||
реакцию в заделке изображают так, как показано на рис. 7.19.
§ 7.6. Теорема Вариньона для сходящейся системы сил
Вектор момент равнодействующей системы сходящихся сил относительно произвольной точки равен сумме векторов моментов всех составляющих сил относительно той же точки.
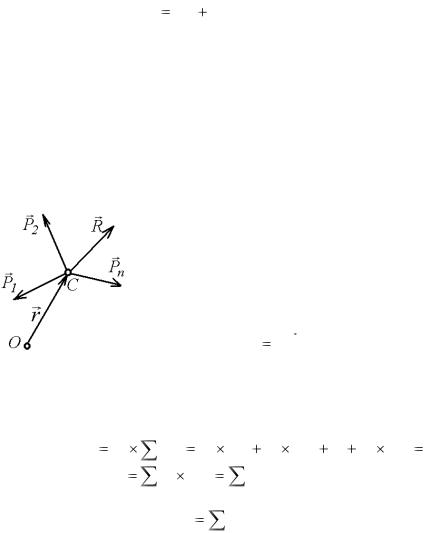
Доказательство. Переносим все силы по их линиям действия в точку пересечения их линий действия С как в общую
точку приложения и находим равнодейст-
вующую всех сил R (рис. 7.20). Выбираем произвольную точку О и проводим
вектор -радиус r OC . У всех сил, вклю-
чая их равнодействующую R , векторра- диус будет одинаков. Используя свойства векторного произведения, а также форму-
лы (7.7) и (7.17) получаем
|
|
|
|
|
|
|
|
|
|
|
|
M0 |
( R ) ( r |
Pk |
) ( r P1 ) ( r P2 |
) |
( r Pn ) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( r Pk ) |
|
M 0 |
( Pk ), |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0 ( R ) |
M |
0 ( Pk ) . |
|
|
|
(7.27) |
||
Если все сходящиеся силы расположены в одной плоскости и точка О (центр моментов) находится в той же плоскости,
130

то все векторы моменты сил будут расположены на одной прямой, проходящей через точку О, и перпендикулярной к плоскости сил. Тогда, согласно (7.9), векторное суммирование моментов можно заменить алгебраическим суммированием. Получаем частный случай доказанной теоремы.
Вектор момент равнодействующей плоской системы сходящихся сил относительно произвольной точки в плоскости расположения сил равен алгебраической сумме моментов всех составляющих сил относительно той же точки
|
|
|
M0 ( R ) |
M0 ( Pk ) . |
(7.28) |
Теорема 7.4. Величина момента равнодействующей системы сходящихся сил относительно некоторой оси равна сумме величин моментов всех составляющих сил относительно той же оси.
Доказательство. Спроецируем равенство (7.30) на произвольную ось l, проходящую через точку О и при этом воспользуемся двумя теоремами: о проекции векторной суммы на ось, см. (7.7), и о связи между величинами моментов силы относительно оси и вектором моментом силы относительно какой - либо точки на этой оси, см. (7.25),
|
|
|
|
|
прl M 0 |
( R ) |
прl M 0 |
( Pk |
) . |
Тогда, |
|
|
|
|
|
|
|||
M01( R ) |
M01( Pk ) . |
(7.29) |
||
Теорема доказана.
Рассмотренные теоремы верны и для произвольной системы сил. Доказательство применимости теоремы Вариньона к произвольной системе сил рассмотрено в гл 9.
131

§ 7.7. Задачи для самостоятельного решения
7.1.Как соотносятся между собой модули векторов сил
иP2 , если угол между ними равен 135 , а модуль равно-P
|
действующей этих сил равен модулю мень- |
|||||
|
шей силы? |
|
|
|||
|
|
7.2. Определить модуль и направление |
||||
|
равнодействующей |
плоской системы сил |
||||
|
|
|
|
|
|
|
Рис. 7.21 |
P1 , |
P2 , |
P3 |
и P4 (рис. 7.21), приложенных в |
||
точке А, если P1 = P4 = 100 Н, P2 = 120 Н, |
||||||
|
||||||
|
P3 = 80 Н и если |
|
||||
|
известны |
|
углы |
|
||
|
между этими си- |
|
||||
|
лами |
|
= |
30 , |
|
|
|
= |
45 , |
= |
|
||
Рис. 7.22 |
330 . |
|
|
|
||
|
|
7.3. |
|
|||
|
|
|
|
|||
делить силы натяжения тросов АВ и |
|
|||||
СВ (рис. 7.22), на которых висит |
Рис. 7.23 |
|||||
груз массой m = 10 |
кг, |
если |
|
|||
АВС= 120 . Веса тросов не учитывать.
7.4. Фонарь массой m = 17 кг подвешен к середине троса длиной l 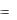 20 м (рис. 7.23). Трос провисает на h = 0,5 м. делить силу натяжения троса. Как изменится сила натяжения
20 м (рис. 7.23). Трос провисает на h = 0,5 м. делить силу натяжения троса. Как изменится сила натяжения
|
троса, если стрела провеса была бы вдвое |
|
|
меньше? |
|
|
7.5. |
На прямоугольном кронштейне |
|
(рис. 7.24) висит груз массой m = 2 кг. Сила, |
|
|
сжимающая стержень АВ равна 25 Н. Каков |
|
Рис. 7.24 |
угол |
? |
|
|
|
132
7.6. Веревка DABC, перекинутая через блок, закреплена одним концом С неподвижно (рис. 7.25).
Ко второму концу D этой веревки подвешен груз массой m . Найти силу давления, передаваемую через блок на ось блока и угол, который эта сила образует с горизонталью. Угол 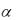 между веревкой ВС и горизонталью известен.
между веревкой ВС и горизонталью известен.
|
|
|
|
7.7. |
|
Рис. 7.25 |
||
|
|
|
|
|
|
|
|
|
|
|
К вершине О прямой треуголь- |
||||||
|
|
ной призмы (рис. 7.26) |
прило- |
|||||
|
|
|
|
|
|
|
|
|
|
|
жены |
пять |
сил P1 , |
P2 |
,…. P5 . |
||
|
|
|
|
|
|
|
|
|
|
|
Сила |
P4 направлена по диаго- |
|||||
|
|
|
|
|
|
|
|
|
|
|
нали ОВ грани ОАВС, |
силы P1 , |
|||||
|
|
|
|
|
|
|
|
|
|
|
P2 , |
P5 - по ребрам ОD, ОС, ОА, |
|||||
|
|
|
|
|
|
|
|
|
|
Рис. 7.26 |
а сила P2 |
лежит в плоскости |
|||||
|
|
грани ОDC и составляет с |
||||||
|
|
ребром OD угол 30 . Определить |
||||||
|
|
модуль и направление равнодей- |
||||||
|
|
ствующей системы сил, |
если P1 = |
|||||
|
|
P3 = 100 Н. |
|
|
|
|
||
|
|
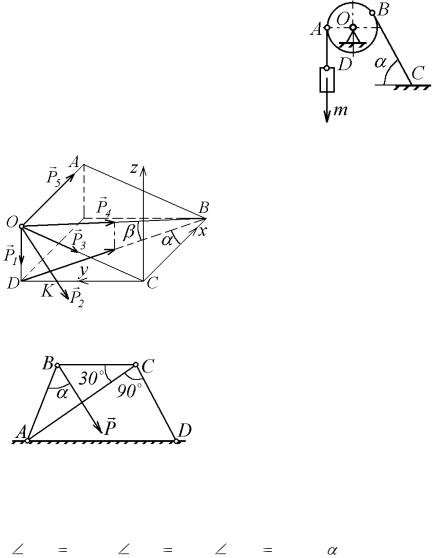
7.8. К узлу В шарнирно- |
||||||
|
Рис. 7.27 |
стержневого |
четырехугольника |
|||||
|
ABCD (рис. 7.27), сторона AD ко- |
|||||||
|
|
|
|
|
|
|
|
|
торого закреплена неподвижно, приложена сила P . Найти си- |
||||||||
лы, |
передающиеся на |
стержни АС и DС, |
если P = |
2 кН, |
||||
ABC 120 , BCA |
30 , ACD |
90 , |
и |
=60 . |
|
|
||
|
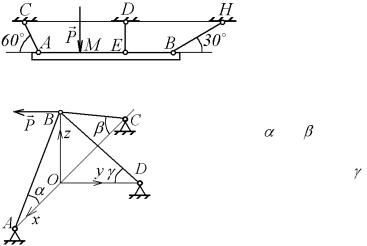
7.9. К горизонтальной балке АВ, подвешенной на трех |
|||||||
канатах АС, ED и ВН, составляющих с прямой АВ угла 120 , |
||||||||
90 |
и 30 (рис. 7.28), в точке М приложена вертикальная сила |
|||||||
|
|
133 |
|
|
|
|
|
|
|
|
|
|
|
|
|
P , равная 0,8 кН. Определить силы, растягивающие канаты, |
||||||
|
если АМ= МЕ= ЕВ= 1 м. |
|||||
|
|
7.10. Три невесомых |
||||
|
стержня соединены меж- |
|||||
|
ду |
собой |
в |
точке |
В |
|
Рис. 7.28 |
(рис.7.29). Стержни АВ и |
|||||
|
ВС лежат в координатной |
|||||
плоскости zОx и их оси составляют с |
||||||
осью х углы |
и |
, |
а стержень BD |
|||
расположен в плоскости zOy и его ось |
||||||
составляет с осью Оу угол |
. К узлу В |
|||||
|
|
|
|
|
|
|
приложена сила P |
параллельная оси |
|||||
|
|
|
|
|
|
|
у. |
Определить |
силы N1 , |
N2 и |
N 3 , |
||
действующие на стержни. Какие из
этих стержней сжаты, а какие – растяРис. 7.29 нуты.
134

Глава 8. УСЛОВИЯ РАВНОВЕСИЯ АБСОЛЮТНО
ТВЕРДОГО ТЕЛА
§ 8.1. Приведение произвольной пространственной системы сил к двум силам
Для сил системы, состоящей из n сил, введем обозначе-
ние P1 ,P2 , ,Pn . Силу с порядковым номером k обозначим
символом Pk .
Главным вектором произвольной системы сил называют вектор, равный векторной сумме всех сил системы
V0 |
Pk . |
(8.1) |
Индекс О означает, что главный вектор приложен к точке
О.
Главным моментом произвольной системы сил относительно данной точки О называют сумму векторов моментов всех сил системы относительно этой точки
M0 M0 ( Pk ) |
(8.2) |
Воздействие сил на тело является объективным процессом. В результате непротиворечивых операций с силами, как с векторами, можно получить из данной системы сил несколько других систем сил. Преобразование одной системы сил в другую является субъективным процессом, поскольку отражает принятие решений какие операции и с какими векторами производить. Однако, изменение описания какого либо процесса не может изменить результат, достигаемый процессом. Поэтому такие преобразования систем сил не могут изменить воздействия на тело, то есть исходная система сил и системы сил, полученные в результате преобразований, будет действовать на тело одинаково.
135
