
Учебное пособие 1692
.pdfплоскости сил, равен алгебраической сумме моментов всех сил системы относительно того же центра.
Используя доказанную теорему, можно получить важные теоремы - следствия.
§ 9.2. Теория пар сил
Из теоремы об эквивалентности систем сил получается, как следствие, теория пар сил.
Теорема 9.2. Пара сил не имеет равнодействующей. Доказательство. Согласно (9.1) главный вектор пары ра-
вен нулю, а главный вектор V одной силы равен этой силе. Поэтому на основании теоремы об эквивалентности систем сил пара не эквивалентна одной силе. Итак, пару нельзя упростить, заменив одной силой. Пара, как и одна сила, есть самостоятельный, первичный элемент силового воздействия на тело.
Теорема 9.3. Две пары эквивалентны, если равны их векторы моменты.
Доказательство. Согласно (9.2) и теореме 7.1, сформулированной в (гл. 7), главный момент пары равен вектору моменту пары. Так как по условию теоремы векторы моменты двух пар равны, то равны и их главные моменты. Главные векторы всех пар равны всегда, поскольку каждый из них равен нулю. В силу теоремы об эквивалентности эти пары эквивалентны, что и требовалось доказать.
Из этой теоремы получаются как следствия следующие теоремы, истинность которых обусловлена тем, что главные моменты пар остаются неизменными (инвариантными) векторными величинами.
186
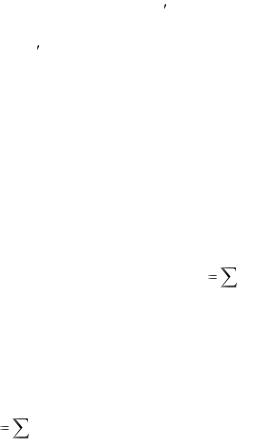
Теорема 9.4. Пару сил, не нарушая ее действия на твердое тело, можно переносить из одной плоскости в другую, ей параллельную плоскость.
Теорема 9.5. Две пары в плоскости эквивалентны, если равны их моменты. Следовательно, пару можно заменить эквивалентной парой, действующей в той же плоскости и имеющей одинаковые с первой парой направление вращения и величину момента.
Примечание. Величины сил пары P и P можно изменять, но так, чтобы оставалось постоянным произведение Ph.
Например, если силы P и P увеличить в m раз, то плечо h надо уменьшить также в m раз. Таким образом, не меняя действия пары на твердое тело, ее можно поворачивать в плоскости пары и перемещать в своей плоскости, менять плечо пары, менять модули сил пары, но все это можно делать при условии сохранения постоянным модуля момента пары Ph и направления вращения пары.
Теорема 9.6. Система пар, расположенных в пересекающихся плоскостях, эквивалентна одной паре, вектор момент которой равен сумме векторов моментов всех составляющих пар.
|
|
Доказательство. Возьмем пару с моментом m |
mk , |
где mk - вектор момент k- й пары (k = 1, 2 ...). Так как главный
момент пары равен ее вектору моменту, то имеем равенство главных моментов заданной системы пар и взятой нами одной пары. Главные векторы, как величины равные нулю, также равны. Теорема доказана. Условия теоремы об эквивалентных системах сил удовлетворены. Следовательно,
|
|
|
m |
mk . |
(9.6) |
Если система пар плоская, то все векторы моменты пар можно расположить вдоль одной прямой, перпендикулярной
187
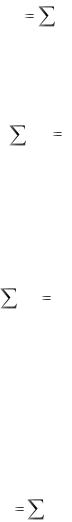
плоскости пар, и тогда, как известно, векторное суммирование можно заменить алгебраическим. Следовательно, система пар, расположенных в одной плоскости, эквивалентна одной паре, величина момент которой равен сумме величин моментов всех составляющих пар
m |
mk . |
(9.7) |
Теорема 9.7. Для равновесия твердого тела под действием системы пар, расположенных в пересекающихся плоскостях, необходимо и достаточно, чтобы сумма векторов моментов этих пар равнялась нулю
|
|
|
mk |
0 . |
(9.8) |
Доказательство этой теоремы весьма просто получается из теоремы 9.6.
Теорема 9.8. Для равновесия твердого тела под действием системы пар, расположенных в одной плоскости, необходимо и достаточно, чтобы сумма величин моментов этих пар равнялась нулю:
mk 0 . |
(9.9) |
Эта теорема широко применяется при изучении плоских систем сил и является частным случаем теоремы 9.7.
§ 9.3. Теорема Вариньона для произвольной системы сил
Момент равнодействующей произвольной пространственной системы сил относительно любой точки равен векторной сумме моментов всех слагаемых сил относительно той же
точки: |
|
|
|
|
|
|
|||
M0 |
( R ) |
M0 |
( Pk ) |
(9.10) |
188
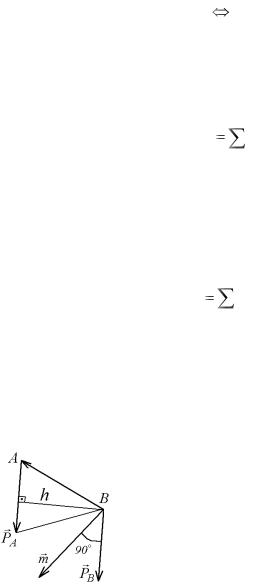
Доказательство. Итак, R ( P1 ,P2 , ,Pn ), т.е. одна сила
эквивалентна заданной системе сил. В силу теоремы об эквивалентности, главные моменты этих систем равны. Так как главный момент одной силы (равнодействующей) относительно любой точки равен моменту этой силы относительно той же точки, то
|
|
|
|
M0 |
( R ) |
M0 |
( Pk ) . |
Теорема доказана.
В частности, когда система сил плоская и центр моментов О находится в плоскости расположения этих сил, то все векторы моменты будут расположены параллельно одной прямой, перпендикулярной плоскости сил, и векторное суммирование моментов можно заменить алгебраическим:
|
|
|
M0 ( R ) |
M0 ( Pk ) . |
(9.11) |
Итак, момент равнодействующей произвольной плоской системы сил относительно любой точки в плоскости этих сил равен алгебраической сумме моментов всех слагаемых сил относительно той же точки.
§9.4. Приведение произвольной системы сил
кданному центру
Центром приведения О называется точка приложения главного вектора системы сил (см. (§ 9.1)].
Теорема 9.9 о параллельном переносе силы. Силу, не меняя ее действия на абсолютно твердое тело, можно перенести па-
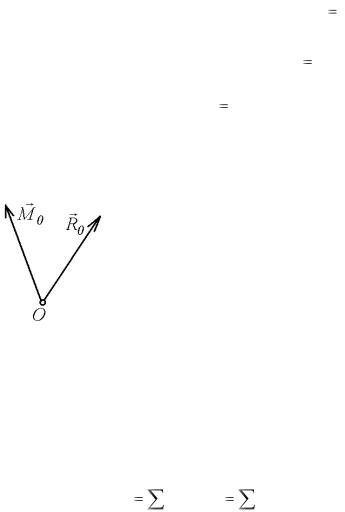
Рис. 9.1 раллельно самой себе в произвольный центр приведения, но, при этом, надо приложить к
189
телу пару сил с моментом, равным моменту силы относительно ее новой точки приложения (центра приведения).
Доказательство. Пусть дана сила PA , приложенная в точ-
ке А (рис. 9.1). Возьмем систему, состоящую из силы PB , приложенной в произвольной точке В, равную по модулю силе
|
|
|
|
|
PA , ей параллельной и одинаково с ней направленной, и, кро- |
||||
|
|
|
|
|
ме того, возьмем пару с вектором моментом |
m |
M B ( PA ) . То- |
||
гда по теореме об эквивалентности: сила |
|
будет эквива- |
||
P |
||||
|
|
A |
|
|
лентна силе PB |
и паре сил с моментом m |
M B ( PA ) , так как |
||
равны главные векторы этих систем и их главные моменты от-
носительно точки В. Модуль |
|
|
|
|
|
|
m |
M |
|
( P ) = Ph (рис.9.1). Плос- |
|||
|
|
|
|
B |
A |
|
кость пары m |
лежит в плоскости сил |
PA и |
PB . |
|||
Теорема доказана.
Теорема 9.10 о приведении системы сил к главному вектору и главному моменту.
Произвольная пространственная система сил эквивалентна одной силе, приложенной в произвольно выбранном центре приведения О и равной главному вектору системы и одной паре, момент которой равен главно-
Рис. 9.2 му моменту системы относительно центра приведения О (рис. 9.2).
|
|
|
|
|
|
|
|
Доказательство. Пусть дана система сил ( P1 ,P2 |
, ,Pn ) . |
||||||
Возьмем силу V0 , приложенную в произвольной точке О и |
|||||||
|
|
|
|
|
|
|
|
равную главному вектору заданной системы ( P1 |
,P2 |
, ,Pn ) и |
|||||
|
|
|
|
|
|
|
|
пару с моментом m0 |
, равным главному моменту заданной сис- |
||||||
темы сил относительно точки О |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
V0 |
Pk |
M0 |
M0 |
( Pk ) . |
|
|
(9.12) |
|
|
190 |
|
|
|
|
|

Очевидно, что главный вектор силы равен самой силе, а главный момент пары равен моменту пары. В силу теоремы об эквивалентности систем сил получаем, что система сил
|
|
|
|
|
|
|
( P ,P , ,P ) |
эквивалентна силе |
V |
|
и паре сил с моментом |
||
1 |
2 |
n |
|
|
O |
|
M0 .
Теорема доказана.
Если система сил плоская и центр приведения О лежит в плоскости расположения сил, то система сил эквивалентна одной силе - главному вектору системы и одной паре, момент которой равен главному моменту системы сил, равному сумме величин моментов всех сил системы относительно центра при-
ведения О |
|
|
|
|
|
M 0 |
M 0 ( Pk ) . |
(9.13) |
Из равенства (9.12) следует, что главный вектор системы сил не зависит от центра приведения (от своей точки приложения).
Рис. 9.3
Рис. 9.4
§ 9.5. Задачи для самостоятельного решения
9.1. Даны три силы P1 , P2 и
P3 , приложенные в точках А1(0; 2; 1), А2(1; -1; 3), А3(2; 3; 1) и их про-
|
|
екции на оси координат P1 (3; 5; 4), |
|
|
|
P2 (-2; 2; -6), |
P3 (-1; -7; 2). Координа- |
ты точек даны в метрах, а проекции – в ньютонах. Привести эту систему сил к началу координат.
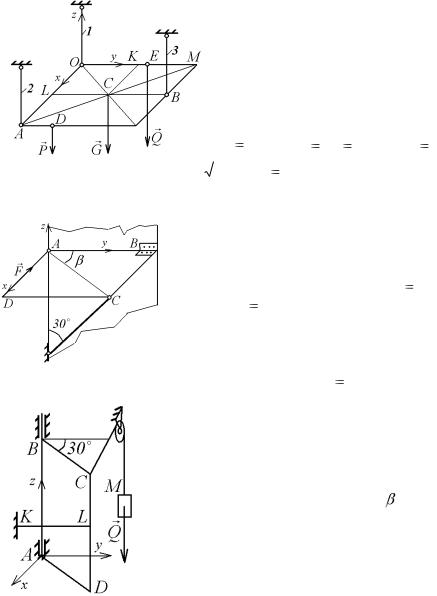
9.2. По ребрам призмы (рис. 9.3), для которой ОА= 2ОК= 20 см,
= 30 |
действуют силы P = 40 Н, |
|
1 |
P2 P5 |
10 Н, P3 15 Н, P4 = 5 Н. |
191
|
|
Привести эту систему сил к про- |
|||||||
|
|
стейшему виду. |
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
9.3. Дана система сил |
P1 , |
P2 , |
||||
|
|
|
|
|
|
|
|||
|
|
P3 , P4 , P5 , приложенных в вер- |
|||||||
|
|
шинах прямоугольного паралле- |
|||||||
|
|
лепипеда и направленных в со- |
|||||||
|
|
ответствии с рис. 9.4, причем |
|
||||||
|
|
P1 |
60 Н, P2 P3 |
10 Н, P4 |
|
||||
|
|
|
|
|
|
||||
Рис. 9.5 |
10 5 |
|
Н, P5 |
20 Н, ОА= ОВ= 20 см, |
|||||
ОС= 10 см. Привести эту систему к |
|||||||||
|
|||||||||
|
простейшему виду. |
|
|
|
|||||
|
9.4. Однородная прямоугольная |
|
|||||||
|
плита (рис. 9.5) веса G = 300 Н подве- |
||||||||
|
шена на трех вертикальных тросах. К |
||||||||
|
плите подвешены грузы весом P |
|
|||||||
|
200 Н и Q 100 Н. Определить силы |
||||||||
|
натяжения тросов, если АL= LO= 20 |
||||||||
|
см, OE= 60, EM= 40 см. |
|
|
|
|||||
|
9.5. К однородной прямоугольной |
||||||||
Рис. 9.6 |
плите (рис. 9.6) веса Q |
15 Н, удер- |
|||||||
|
живаемой в горизонтальном положении |
||||||||
|
сферическим шарниром А, петлей (цилин- |
||||||||
|
дрическим шарниром) В и стержнем КС, |
||||||||
|
приложена горизонтальная сила F = 30 Н. |
||||||||
|
Определить сжимающую силу N в |
|
|
||||||
|
стержне КС и реакции опор, если |
= 30 . |
|||||||
|
9.6. Однородная прямоугольная дверь |
||||||||
|
веса P = 300 Н (рис. 9.7) укреплена с по- |
||||||||
|
мощью подпятника А и петли В. Дверь |
|
|||||||
Рис. 9.7 |
удерживается в приоткрытом положении |
|
двумя веревками, одна из которых СМ на- |
||
|
||
тягивается грузом, вес которого Q = 100 Н, а другая прикреп- |
||
лена в точке К к стене и расположена параллельно координат-
192
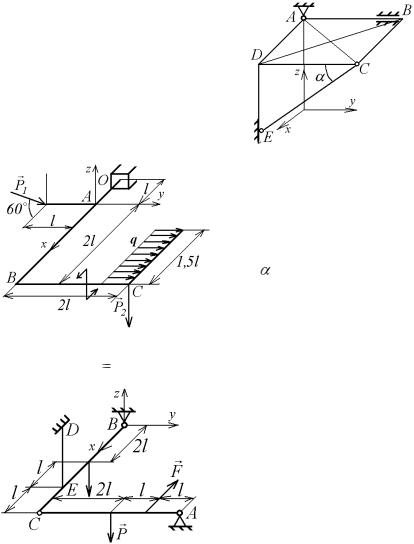
ной оси у. Определить силу натяжения веревки KL и реакции опор,
если ВС= АВ/3= 1 м, DL= LC.
9.7. Квадратная однородная полка массой m = 8 кг прикреплена к стене с помощью шарового
шарнира А и цилиндрического |
|
|
шарнира В и удерживается в гори- |
||
зонтальном положении однород- |
Рис. 9.8 |
|
|
|
|
|
ным стержнем веса P = 20 Н, |
|
|
соединенным с полкой и сте- |
|
|
ной сферическими шарнирами |
|
|
С и Е (рис. 9.8). Определить |
|
|
реакции шарниров А, В и Е, |
|
|
если = 60 . |
|
|
|
9.8. Заделанный в сте- |
Рис. 9.9 |
|
ну стержень (рис. 9.9) на- |
|
|
гружен равномерно распре- |
деленной нагрузкой q = 60 Н/м, парой сил с моментом |
M = 20 |
Н*м, силой P1 20 Н, расположенной в вертикальной |
плоско- |
сти под углом 60 к горизонтальной плоскости, и вертикальной силой P2 = 10 Н, приложенной к точке С. Опреде-
Рис. 9.10
лить реакцию заделки, если l 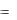
0,5 м.
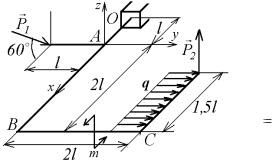
9.9. Два стержня одинаковой длины 4 l = 2м и одинакового веса P  120 Н соединены между собой и с опорами сфери-
120 Н соединены между собой и с опорами сфери-
ческими шарнирами (рис. 9.10). В горизонтальном положении стержни удерживаются тросом DE. К стержню АС приложена сила F  240 Н, которая параллельна оси х. Определить реакции шарниров А и В и силу натяжения T троса.
240 Н, которая параллельна оси х. Определить реакции шарниров А и В и силу натяжения T троса.
193
|
9.10. Заделанный в |
|
|
стену стержень (рис. 9.11) |
|
|
нагружен равномерно рас- |
|
|
пределенной нагрузкой q = |
|
|
60 Н/м, парой сил с момен- |
|
|
том M = 20 Н*м, силой |
|
|
P1 20 Н, расположенной |
|
|
в вертикальной плоскости |
|
|
под углом 60 к горизон- |
|
Рис. 9.11 |
тальной плоскости, и вер- |
|
тикальной силой P2 = 10 Н, |
||
|
приложенной к точке С. Определить реакцию заделки, если l 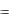 0,5 м.
0,5 м.
194
Глава 10. ЦЕНТР ТЯЖЕСТИ. ГЕОМЕТРИЧЕСКИЕ
ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
§ 10.1. Центр тяжести
Центром тяжести тела называется точка схождения сил тяжести, действующих на тело во всевозможных его положениях.
Определение центра тяжести основано на теории сложения параллельных сил.
10.1.1. Сложение параллельных сил
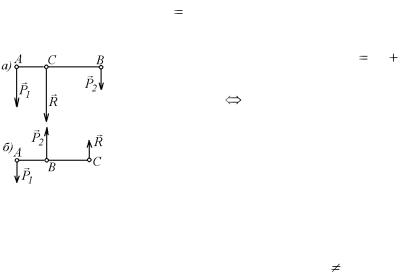
Пусть имеется система из двух параллельных сил P1 и
P2 , направленных параллельно (рис. 10.1).
Пусть точка С расположена так, что
|
|
P1 |
|
BC |
|
|
|
|
|
(10.1) |
|
|
P2 |
AC |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
К точке С приложим силу R P1 |
P2 . |
|||||||
|
Из теоремы об эквивалентных системах сил |
|||||||||
|
|
|
|
|
|
|
|
|
||
|
следует, что R |
( P1 |
,P2 ) . Главные векторы |
|||||||
|
этих систем сил одинаковы, главные момен- |
|||||||||
|
ты относительно точки С также равны. Глав- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ный момент R |
равен нулю, поскольку сила |
||||||||
|
|
|
|
|
|
|
|
|
||
|
R приложена в точке С. Главный момент |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
двух сил |
P и |
P также равен нулю соглас- |
|||||||
Рис. 10.1 |
|
|
|
1 |
|
2 |
|
|
||
|
но (10.1): M0( P1 ) + M0( P2 ) = P1AC — P2BC |
|||||||||
= 0. При одинаковых направлениях сил R= P1+ P2, при противоположных направлениях R = P2 + (-P1), где P2 P1. Следовательно, две параллельные силы, направленные в одну сторону, имеют равнодействующую, параллельную этим силам, и проходящую через точку, которая делит внутренним образом отрезок между точками приложения данных сил на части, обрат-
195
