
Учебное пособие 1692
.pdf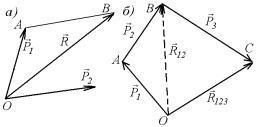
линдрического опорного отверстия.
7.3.3. Связи третьей группы
К связям третьей группы относятся сферический шарнир и подпятник и шероховатая поверхность.
Сферическим шарниром называется соединение двух тел, которое (рис. 7.6, ж) позволяет соединяемым телам вращаться вокруг любой оси, проходящей через центр шарнира. При отсутствии сил трения реакция а шарнире может быть направлена как угодно вдоль прямой, проходящей через неподвижную точку О (центр шарнира) перпендикулярно к сферическим поверхностям соединяемых тел. Направление реакции в сферическом шарнире заранее не известно.
Подпятником (рис. 7.6, з) называется подвижное соединение, образованное цилиндрическими деталями. Чаще всего подпятник состоит из углубления в опорном теле, в которое входит ось опирающегося тела. В подпятнике реакция проходит через ось вращения. Направление и точка приложения реакции заранее не известны.
Шероховатая поверхность относится к связям, для которых направление реакции заранее не известно. Действие такой поверхности на тело зависит от внешних сил и порождаемой
|
ими силы трения |
Рис. 7.7 |
скольжения (см. гл. 8, |
§ 8.4). |
|
Особого рода связью является так называемая «заделка» (см. § 7.5). В зависимости от характера заделки эта связь относится ко второй или третьей группе.
116
§ 7.4 Проекции на ось силы и суммы сил
Основные правила действий с векторами рассмотрены в гл. 1 [6].
Рассмотрим параллелограмм сил (см. рис. 7.7,а). Отрезок
|
|
|
AB равен и параллелен вектору P2 |
. Поэтому, если мысленно |
|
|
|
|
(на самом деле сила P2 приложена в точке О) отложить вектор |
||
|
|
|
силы P |
от конца А вектора силы |
P , то начало равнодейст- |
2 |
|
1 |
вующей |
R будет находится в начале первой силы, а конец - в |
|
конце второй силы. Таково правило силового треугольника
(рис. 7.7,а).
Рассмотрим пучок сил, т. е. систему сил, приложенных в
|
|
|
|
|
|
одной точке (рис. 7.7,б). Складывая силы P |
и |
P по правилу |
|||
|
|
1 |
|
2 |
|
треугольника, |
получаем равнодействующую |
R12 . Затем по то- |
|||
|
|
|
|
|
|
му же правилу складываем R12 и |
P3 и получаем равнодейст- |
||||
|
|
|
|
|
|
вующую R123 |
трех сил. Просуммировав все силы, |
получим |
|||
|
|
|
|
|
|
равнодействующую R всех сил. |
Ломаную |
линию |
OABCО, |
||
звенья которой равны и параллельны данным силам, называют силовым многоугольником. Правило силового многоугольника заключается в следующем: чтобы сложить систему сил, приложенных в одной точке, надо от конца первой силы отложить
вектор второй силы, от конца второй силы отложить вектор
третьей силы и т. д. Вектор равнодействующей R имеет начало в начале первой силы и конец - в конце последней силы.
Сложение сил по правилу параллелограмма называют векторным суммированием. Поскольку правило силового мно-
гоугольника является следствием правила параллелограмма, то
вектор R , замыкающий ломаную линию, изображающую силы, называют векторной суммой сил. В частном случае, когда все силы приложены к телу в одной точке, равнодействующая сил и их векторная сумма совпадают. Однако существуют сис-
117
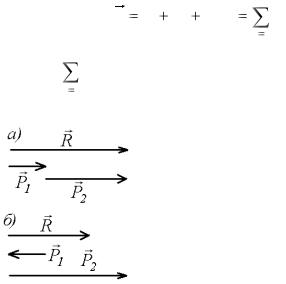
темы сил, для которых равнодействующая, т. е. сила, эквивалентная (по действию) системе сил, и векторная сумма этих сил не эквивалентны по их действию на тело, то есть оказывают разное действие на тело.
Например, если изобразить на рис. 7.7, б вектор R123 с
началом не в точке О, а в какойлибо другой точке, не лежащей на прямой ОС, то в новом положении этот вектор будет векторной суммой всех данных сил, но уже не будет их равнодействующей.
Систему сил, линии действия которых пересекаются в одной точке, называют системой сходящихся сил. Считая, что все силы приложены к твердому телу, перенесем их по линиям действия и приложим в общей точке О пересечения сил - точке схождения сил. Следовательно, неуравновешенная система сходящихся сил имеет равнодействующую силу, приложенную в точке пересечения этих сил (или их продолжений) и равную векторной сумме всех заданных сил
|
|
|
n |
|
R P1 |
P2 |
Pn |
Pk , |
(7.7) |
|
|
k |
1 |
|
n
где знак (сигма) означает сумму, а величина k называется
k 1
индексом суммирования.
Ниже будет показано, что только система сходящихся сил всегда эквивалентна одной силе - равнодействующей. Другие системы сил этого свойства не имеют.
Наиболее проста система сил, состоящая из двух параллельных сил с точками приложения сил, находящихся на одной прямой (рис. 7.8). Очевидно, что,
Рис.7.8 векторная сумма сил, направленных в
118

одну сторону по одной прямой, направлена в ту же сторону (рис. 7.8, а). Ее модуль равен сумме модулей составляющих сил
R P1 P2 . |
(7.8) |
Если силы направлены по прямой в противоположные стороны (рис. 7.8, б), то модуль равнодействующей равен абсолютному значению алгебраической суммы модулей составляющих сил, а равнодействующая направлена в сторону большей по модулю силы
R |
P1 P2 |
. |
(7.9) |
Очевидно, это заключение верно для произвольного числа сил параллельных сил, лежащих на одной прямой.
Из векторной алгебры известна теорема о проекции векторной суммы: проекция векторной суммы сил на какую-либо ось равна сумме проекций составляющих сил на ту же ось
Rl = Pkl, |
(7.10) |
здесь Рkl - проекция силы, с порядковым номером k, на ось l. Проекции силы на оси координат обозначают символами
|
|
|
|
|
|
|
npx Pk |
( Pk )x |
Pk x |
X k , npy Pk |
( Pk )y |
Pk y Yk , |
|
|
|
|
|
|
Zk . |
|
|
|
npz Pk |
( Pk )z |
Pkz |
|
|
Приняв за оси для проецирования координатные оси, согласно (7.10) получаем
Rx= Xk; Ry= Yk; Rz= Zk. |
(7.11) |
Проекции вектора определяют его величину (модуль) и направление согласно формулам
R Rx2 Ry2 Rz2 |
(7.12) |
119
cos |
Rx |
R , cos |
Ry R, cos |
Rz R, (7.13) |
|
где , и - углы |
|
с осями координат. |
|
||
R |
|
||||
К сложению сил, не лежащих в одной плоскости, применимо правило параллелепипеда, которое получится, если 2 раза применить правило параллелограмма сил (см. гл. 1).
Рис. 7.9 |
|
Из построения на рис. 7.9 |
||||||
видно, что равнодействующая |
трех сил |
|
, |
|
, |
|
, прило- |
|
R |
P1 |
P2 |
P3 |
|||||
женных в одной точке, приложена в той же точке и равна по величине и направлению диагонали параллелепипеда, ребра которого равны и параллельны заданным силам. Согласно
правилу параллелепипеда заданную силу R можно разложить по трем заданным направлениям l1, l2, l3 единственным образом (рис 7.9)
|
|
|
|
|
R |
P1 |
P2 |
P3 . |
(7.14) |
Если составляющие силы взаимно перпендикулярны, то получается прямоугольный параллелепипед. Проведем оси координат по трем сходящимся ребрам этого параллелепипеда (рис. 7.9). Тогда модули P1, P2, P3 составляющих сил будут равны абсолютным величинам соответствующих проекций равнодействующей силы на эти
оси: |Rx|= P1, |Ry|= P2, |Rz | = P3,
и, следовательно, можно пользоваться формулами (7.12) и (7.13).
Пример 7.3. Найти величину и направление равнодействующей трех взаимно перпендикулярных сил P1 = 15 H, P2 = 10 H, P3 = 6 H, приложенных в одной точке (рис. 7.9).
120
Решение. Согласно правилу параллелепипеда и имея в виду, что Rx = P1, Ry = P2 и Rz = P3 из формулы (7.12) находим
R = 19 H.
Согласно (7.13) cos = 15/19 = 0,7894; cos = 10/19 = 0,5263; cos = 6/19 = 0,3158. Тогда = 37° 53'; = 58° 15'; 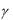 =
=
71° 35'.
Пример 7.4. Даны пять сил, лежащих в одной плоскости, и направленных, как показано на рис. 7.10. Модули этих сил
Рис. 7.10 |
|
|
|
|
|||
равны P1 = 2 H, P2 = 3 2 H, P3 = 4 H, P4 = 5 H, |
|||||||
P5 = 7 H, = 45°. Найти равнодействующую этих сил. |
|||||||
Решение. Из (7.6) и (7.11) следует |
|||||||
Rx = P2 |
cos |
+ P3 - P5 |
= 0; |
|
|
||
Ry = P1 |
+ P2 cos |
- P4 |
= 0. |
|
|
||
|
|
|
|
||||
Тогда, R = |
R2 |
R2 , = 0. |
|||||
|
|
x |
y |
|
|
|
|
§7.5. Моменты силы и пары. Реакция заделки
Втеоретической механике широко используются вспомогательные понятия - момент силы
имомент пары сил, которые необходимы как для изучения теоретического материала, так и для решения задач.
7.5.1. Момент силы относительно точки
|
|
|
|
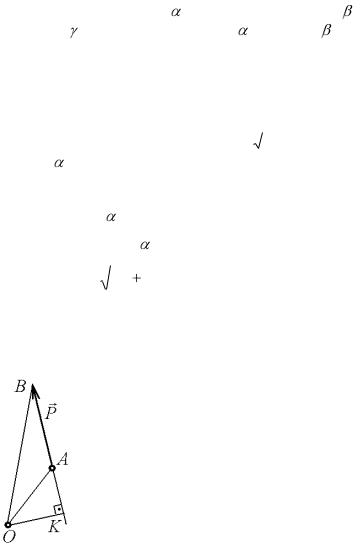
Плечом силы P относительно точки О на- |
|
Рис. 7.11 |
зывают перпендикуляр OK, опущенный из точки |
|
О на линию действия силы (рис. 7.11). |
||
|
||
|
121 |

Величина момента силы P относительно точки О равна алгебраическому значению произведения модуля силы на ее
плечо относительно точки О |
|
|
(7.15) |
Mo ( P ) Ph |
Из (7.15) следует, что момент силы относительно точки не меняется при переносе точки приложения силы по линии ее действия. При определении знака момента следует мысленно считать плечо OK = h стержнем, который закреплен шарнирно
в точке О и имеет свободный конец в точке К. Тогда при вра-
щении плеча под действием силы P вокруг точки О против
часовой стрелки момент будет положительным, а при вращении по часовой стрелке - отрицательным. Если P = 0 или h = 0,
то M0 ( P ) 0 . Итак, момент силы относительно точки О ра-
вен нулю, когда сила равна нулю или когда линия ее действия проходит через точку О. Из рис. 7.11 видно, что
|
|
|M0 ( P )| =2 пл. OAB, |
(7.16) |
т. е. модуль момента силы относительно данной точки численно равна удвоенной площади треугольника, основанием которого является сила, а вершиной - данная точка.
7.5.2.Вектор момент силы относительно точки
Втеоретической механике удобно считать момент силы относительно точки вектором. Определение и основные свойства векторного произведения двух векторов были рассмотрены в [6], § 1.2.
|
Вектором -радиусом точки А при- |
|
|
|
|
Рис. 7.12 |
ложения силы P относительно точки О |
|
называют вектор r , проведенный из точ- |
||
|
ки О в точку А (рис. 7.12).
Точку О, относительно которой определяется момент си-
122
лы, называют центром момента.
Вектором моментом силы P относительно точки О называют вектор, равный векторному произведению вектора - радиуса точки приложения силы на вектор силы
|
|
|
|
(7.17) |
Mo ( P ) |
r |
P |
||
Итак, модуль вектора момента силы относительно данной точки численно равен удвоенной площади треугольника, основание которого соответствует силе, а вершина данной точке (рис. 7.12)
| M o ( P )| 2пл OAB .
Если вектор силы P переносить по ее линии действия, то площадь OAB меняться не будет, и, следовательно, момент силы относительно данной точки не меняется, если силу переносить по ее линии действия.
В некоторых случаях, когда определение плеча силы относительно точки О затруднено, удобно использовать формулы, выражающие проекции вектора – момента M на оси некоторой системы координат через проекции на эти оси вектора си-
ложения силы r :
лы P и векторарадиуса точки при-
M x ry Pz rz Py , M y rz Px rx Pz , M z rx Py ry Px . (7.18)
7.5.3. Пара сил
Очень важное значение в механике имеет особая система сил, называемая парой сил (или просто парой), Пару сил обра-
зуют две равные по модулю, противоположно направленные |
||
|
|
|
параллельные силы (рис. 7.13): |
P |
P . Расстояние h между |
линиями действия сил пары называют плечом пары.
123
7.5.4. Момент пары сил
Величиной момента пары сил называют алгебраическое значение произведения модуля одной из сил пары на ее плечо
m( P,P ) Ph .
Если плечо h представить твердым стержнем, то при его вращении под действием сил пары против хода часовой стрелки в формуле (7.19) надо ставить знак плюс, а при вращении по ходу часовой стрелки - знак минус. Из рис. 7.13 следует
|
(7.20) |
| m( P,P )| Ph 2 пл ABD |
т. е. модуль момента пары сил численно равен удвоенной площади треугольника, основание которого соответствует одной из сил пары, а вершина находится в любой точке на линии действия второй силы пары.
Рис. 7.14 |
Свободным вектором называ- |
|
ют вектор, который можно, не меняя |
его величины и направления, переносить параллельно самому себе из одной
точки тела в другую. |
|
||
|
Вектором |
моментом |
пары |
|
|
|
|
m( P,P ) называют свободный вектор,
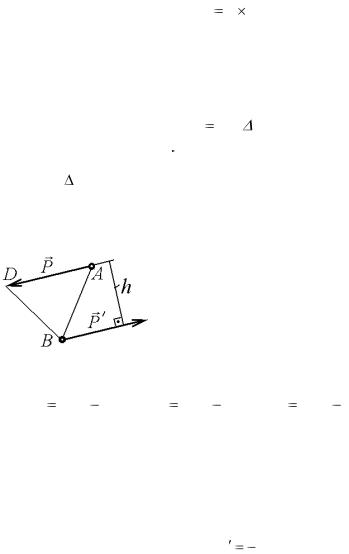
направленный перпендикулярно плоскости пары так, чтобы смотря в направлении, противоположном этому вектору, можно было видеть вращение под действием сил пары против хода часовой стрелки. Модуль момента пары сил равен произведению модуля одной из сил пары на плечо пары (рис. 7.14)
|
|
| m( P,P ) | Ph 2 пл. OAB . |
(7.21) |
124

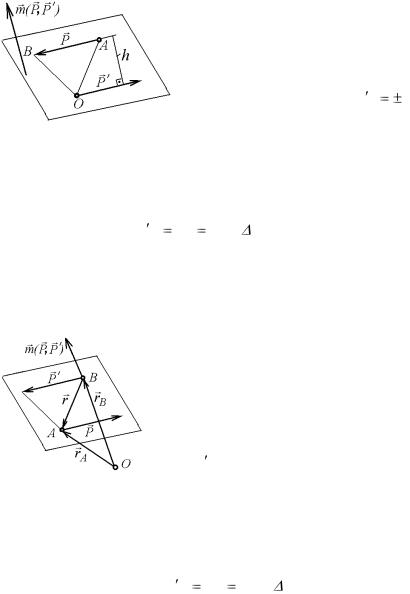
Теорема 7.1. Сумма векторов моментов двух сил, составляющих пару, относительно произвольной точки равна вектору моменту пары.
|
|
|
|
|
|
|
|
|
|
Доказательство. На рис. 7.15 показана пара сил |
( P,P ) , |
||||||
|
|
|
|
|
|
|
|
|
векторы |
BA, rA |
, rB , причем начало О векторов - радиусов |
rA |
|||||
|
|
|
|
|
|
|
|
|
и rB |
точек А и В произвольное. |
Тогда rA |
rB |
BA . |
Отсюда |
|||
|
|
|
|
|
|
|
|
|
BA |
rA |
rB . Учитывая, что P |
P , так как силы P |
и P |
- |
|||
силы одной пары и, используя свойства векторного произведения, получаем
|
|
|
|
|
|
|
|
|
|
|
|
|
M0 ( P ) M0 |
( P ) ( rA |
P ) ( rB |
P ) ( rA |
P ) ( rB |
P ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( rA |
|
P ) ( rB |
P ) [( rA |
rB ) P ] ( BA P ) r P . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С другой стороны M A( P ) |
r P , то есть вектор момент |
||||||||||
пары сил равен вектору моменту одной из сил пары относительно точки приложений второй силы пары.
Следует обратить внимание, что полученное выражение не зависит от положения точки О. Итак, сумма векторов моментов двух сил, составляющих пару, относительно произвольной точки О, равна вектору моменту одной из сил пары относительно точки приложений второй силы пары. Согласно определению вектора момента силы относительно точки и век-
|
|
|
|
|
|
|
тора момента пары M A ( P ) |
m( P,P ) . Следовательно, |
|
||||
|
|
|
|
|
|
|
Рис. 7.15 |
M O ( P ) |
M O ( P ) |
m( P,P ) . |
(7.2 |
||
|
|
|
|
|
|
|
Теорема доказана.
7.5.5. Момент силы относительно оси
Момент силы относительно оси используется для оценки вращательного действия силы вокруг этой оси.
125
