Учебное пособие 516

y = α cosωt +bsinωt = A(sinϕcosωt + cosϕsinωt) =

движения с произвольным периодом T = 2l. Как известно, ряд Фурье такой функции можно записать в виде

называемой основной частотой, записанное разложение может быть представлено в виде

n=1

где

40

A0 = α20 .

Из формулы (2.35) видно, что сложная периодическая функция f(t) вполне определяется совокупностью величин An и ϕn , которые называются соответственно амплитудой и фазой n-й гармоники

An sin(nω1t +ϕn ) функции f(t).

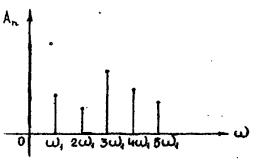
Изобразим спектр периодической функции f(t) графически. Для этого выберем систему координат, назвав ось ординат ось An, а осью абсцисс – осью ω. Так как каждому значению ωn = nω1 соответствует одно вполне определенное значение An, то в этой системе координат спектр представляется как совокупность дискретных точек. Но этот график неудобен.

Поэтому амплитуды отдельных гармоник изображают вертикальными отрезками определенной длины, как показано на рис. 2.13.

Как видим, спектр периодической функции f(t) дискретный. Иногда его также называют линейчатым. В силу того, что частоты гармоник находятся в кратном отношении, спектр состоит из равноотстоящих спектральных линий. Гармонический линейчатый спектр принадлежит периодической функции.

Рис. 2.13.

В приложениях очень часто встречаются задачи, приводящие к нахождению спектра некоторой периодической

41

функции f(t). При этом приходится иметь дело со спектрами самых разнообразных величин. Ведь теми или иными функциями времени могут выражаться изменения различных физических величин.

Нахождение спектра периодического процесса и составляет его гармонический анализ.

Изучая спектр An, функции f(t), легко найти те значения ω, которым соответствуют большие значения An, т.е. те частоты, которым соответствуют гармонические функции, играющие наибольшую роль в образовании данной функции f(t) рядом Фурье.

Преобразование функции f(t) некоторой физической системой является одной из важных практических задач. Решению ее во многом способствует знание спектральных представлений.

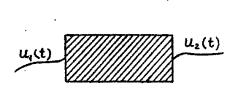
Для определенности рассмотрим какую-нибудь электрическую систему. В эту систему постоянно поступают входные данные (воздействия); система перерабатывает их и непрерывно выдает результат (реакция системы). В нашем случае в качестве воздействия можно считать, например, непрерывно меняющееся направление u1(t), в качестве реакции системы – напряжение u2(t) (рис. 2.14).

Рис. 2.14.

При исследовании системы, в первую очередь, решается основная задача: по заданному воздействию u1(t) определить реакцию системы. С этой целью внешнее воздействие при помощи гармонического анализа представляется суммой элементарных гармонических составляющих, т.е. временная картина заменяется рядом синусоид (спектром). Зная частотные характеристики системы, можно определить

42

изменения вследствие реакции системы каждой из синусоид по амплитуде и по фазе. Сумма измененных синусоид (синтез) даст картину искомого напряжения u2(t) на выходе системы.

В заключении отметим, что если периодическая функция f(t) период T представлена рядом Фурье в комплексной форме:

f (t) = 1 +∞ C Aiω1nt ,

2 ∑−∞ n

то комплексные коэффициенты Cn будем называть совокупностью комплексных амплитуд ряда Фурье. Совокупность модулей комплексных коэффициентов Фурье и будет давать амплитудный спектр данной периодической функции.

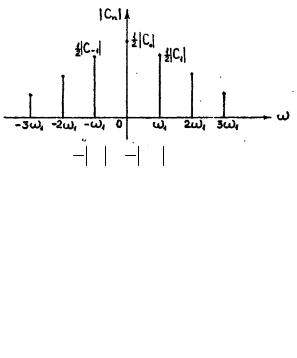
Отметим, что в силу того, что

12 Сn = 12 С−n ,

можно сделать вывод, что амплитудный спектр симметричен относительно оси ординат (рис. 2.15).

Рис. 2.15.

43

Задачи для самостоятельного решения

в ряд по косинусам на [0; π].

3.Разложить функцию f(x)= 10 – x в ряд Фурье на (-5; 5).

4.Разложить функцию f(x)= е x в ряд по синусам на интервале

(0; ln2).

5.Разложить функцию f(x)=cos ax в ряд Фурье в комплексной

форме на интервале (-π; π), ( а – нецелое число).

в ряд по косинусам на [0; π].

3. Разложить функцию f(x)= е x- 1 в ряд Фурье на (-2; 2).

интервале (0; 2).

5. Разложить функцию f(x)=ch x в ряд Фурье в комплексной форме на отрезке [-π; π].

44

45

46

[-π; π].

2. Разложить функцию f(x)= sin ax в ряд Фурье по косинусам на [0; π], ( а – нецелое число).

1 , −1 ≤ x < 0

3. Разложить функцию f (x) = 1/ 2 , x = 0 в ряд Фурье на

x , 0 < x ≤1

[-1; 1].

косинусам на отрезке [0; 2].

5. Разложить функцию f(x)= sh x в ряд Фурье в комплексной форме на интервале (-π; π).

2.Разложить функцию f(x) = π −42x в ряд по синусам на [0; π].

3.Разложить функцию f(x)= 2 x – 3 в ряд Фурье на (-3; 3).

комплексной форме на интервале (-2; 2).

47

на отрезке [0; 4].

5. Разложить функцию f(x)= sin ax в ряд Фурье в комплексной форме на интервале (-π; π), ( а – нецелое число).

Вариант 10

косинусам на [0; π].

(-1; 1).

4.Разложить функцию f(x)= e x в ряд по косинусам на интервале (0; ln2).

5.Разложить функцию f(x)= x sin x в ряд Фурье в комплексной

форме на интервале (-π; π).

48

Вариант 11

синусам на отрезке [0; 3].

5. Разложить функцию f(x)= sin x в ряд Фурье в комплексной форме на интервале (-π; π).

2.Разложить функцию f(x) = x (π - x) в ряд по синусам на (0; π).

3.Разложить функцию f(x)= 4 – 2 x в ряд Фурье на (-4; 4).

комплексной форме на интервале (-π;π).

49