Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 516

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

455.79 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Для решения задачи нам необходимо воспользоваться формулами (2.14) и (2.15), где надо принять l = 2,

														f (x) = x −																		x2					.
Тогда														f (x) = x −																			2				.
																																	2

			2 l																2								1 2																		x2					1 3						2		2
			2 l																2								1 2																		x2					1 3						2		2
α0	=			∫ f (x)dx = ∫(x −																									x )dx =																			−				x					=		;

			l																								2																				2			6						0		3
			l	0															0								2																				2			6						0		3
αn	=		2	∫l			f (x) cos									nπx						dx = ∫2											(x −									1		x2 ) cos							nπx			dx.
αn	=		l	∫l			f (x) cos															dx = ∫2											(x −							2				x2 ) cos										dx.
			l	0															2											0										2												2
Интегрируем по частям:																																									nπx
												1					2																								nπx
			u = x							−				x					,							dv = cos																					dx,
			u = x							−				x					,							dv = cos																					dx,
												2																							2								2nπx
			du = (1 − x)dx,																								v =												sin										,
			du = (1 − x)dx,																								v =							nπ					sin								2		,
																																		nπ													2
			2								1				2										nπx						2									2 2						(1 − x)sin								nπx				dx =.
			2								1				2										nπx						2									2 2														nπx
αn =							x −						x					sin													0				−
αn =			nπ				x −				2		x					sin												2					−																				2
			nπ								2																			2								nπ ∫0																	2
		= −				2			∫2	(1 − x)sin														nπx					dx.
		= −			nπ				∫2	(1 − x)sin																			dx.
					nπ			0																		2
Еще раз интегрируем по частям:
																											nπx
u =1 − x,													dv = sin																					dx,
u =1 − x,													dv = sin																					dx,
																					2							2nπx
du = −dx,											v = −															cos												,
du = −dx,											v = −									nπ						cos							2					,
																				nπ													2
αn	=			4				(1		− x)cos											nπx							2		+							4								2	cos			nπx				dx =.
																																													2

			n2π2																				2					0							n2π2 ∫0															2
			n2π2																				2					0							n2π2 ∫0															2
= −			4				cos nπ −													4							= −									4							[1 + (−1)n ].
= −			2		2		cos nπ −													2			2				= −					n				2			2				[1 + (−1)n ].
		n π																n			π											n					π

Итак,

∞

+ (−

nπx

f (x) =

−

∑

cos

π n =1

8 1

−

cosπx +

cos 2πx +

cos3πx +... .

π2 22

Пример № 9. Разложить в ряд Фурье функцию f(x),

определенную следующим образом

0, - 2 < x ≤0,

f (x) =

x, 0 < x < 2,

Решение. Здесь функция задана на интервале ( - l,

l ), где

l =2. Периодически продолжив заданную функцию на всю числовую ось, получим периодическую функцию периода

T = 2l = 4, рис. (2.10).

Рис. 2.10.

Для решения задачи воспользуемся формулами (2.10’) - (2.11’), положив в них l =2. Тогда

		1 2							1	0			1		2			1 x2		2
α0	=				f (x)dx =						0dx +					xdx =					=1;
α0	=	2 −∫2			f (x)dx =				2		0dx +		2 ∫0			xdx =		2 2		0	=1;
		2 −∫2							2	−∫2			2 ∫0					2 2		0
		1	2					nπx				1		0			nπx
αn	=		∫		f (x)cos						dx =			∫0cos					dx +
αn	=	2	∫		f (x)cos				2		dx =	2		∫0cos				2	dx +
		2	−2						2			2		−2				2
2				nπx					1	2		nπx
+ ∫xcos						dx	=			∫x cos						dx =
+ ∫xcos					2	dx	=		2	∫x cos				2		dx =
0					2				2	0				2

																															nπx
u = x,																	dv = cos																					,
u = x,																	dv = cos																2					,
																			2														2
																			2												nπx
du = dx,														v =											sin													,
du = dx,														v =					nπ						sin								2					,
																			nπ														2
	1						2									nπx						2								2					2							nπx
	1						2									nπx						2								2					2							nπx
=											xsin											0			−										∫sin										dx		=
=	2				nπ						xsin				2										−				nπ						∫sin								2		dx		=
	2				nπ										2														nπ						0								2
	1						4								nπx						2								1						4
=	1						4					cos			nπx						2			=					1						4				(cos nπ −cos0) =

				2						2					2						0													2				2
	2 n						π								2						0								2 n						π
=		2							[(−1)n −1].
=	n		π				2		[(−1)n −1].
		2					2
Итак,								2						[(−1)n −1], (n = 1, 2, …).
αn =								2
αn =						n			π			2
								2				2
Здесь учтено, что cos nπ = (−1)n .
Далее
				1				2												nπx																1				0						2			nπx
bn =								∫ f					(x)sin														dx =													∫0dx + ∫xsin										dx	=
bn =								∫ f					(x)sin								2						dx =									2				∫0dx + ∫xsin									2	dx	=
				2 −2																	2															2		−2								0			2
	1	2											nπx
=	1		∫x sin										nπx				dx =
=			∫x sin														dx =
	2	0											2
																														nπx
u = x,																	dv = sin																				dx,
u = x,																	dv = sin															2					dx,
																							2									2
																							2											nπx
du = dx,														v = −														cos												,
du = dx,														v = −								nπ						cos								2				,
																						nπ														2
	1									2								nπx								2								2				2						nπx
	1									2								nπx								2								2				2						nπx
=			−											x cos												0			+									∫cos								dx		=
=	2		−					nπ						x cos					2										+			nπ						∫cos							2	dx		=
	2							nπ											2													nπ						0							2

	1									2				2cos nπ																4											nπx				2
	1									2																				4											nπx				2
=			−																				+													sin										,
=			−																				+				n2π							2		sin										,
	2							nπ																										2							2				0
	2							nπ																																	2				0

bn = − n2π (−1)n .

Подставляя найденные значения коэффициентов α0, αn, bn в ряд (2.10’) и учитывая, что l = 2, получим

∞

−1

nπx

∞

sin

nπx

f (x) =

∑

(−1)

cos

−

∑(−1)n

n=1

или в развернутом виде

πx

3πx

5πx

cos

+...

f (x) =

−

πx

2πx

3πx

4πx

sin

−

sin

−

sin

+... .

2.2. Ряд Фурье в комплексной форме. Спектральный анализ периодических функций.

2.2.1. Ряд Фурье в комплексной форме.

Для периодической функции f(x) с периодом T = 2π ее разложение в ряд Фурье имеет вид

f (x) = α0 + ∑∞ (αn cos nx +bn sin nx), (2.27) 2 n=1

где

		1	π	f (x)cos nxdx
			π
αn	=				(n = 0,1,2...),
αn	=	π −∫π			(n = 0,1,2...),
		π −∫π				(2.28)
		1	π			(2.28)
		1	∫
bn	=	π −π		f (x)sin nxdx	(n = 0,1,2...).
		π −π

В приложениях часто пользуются другой, более компактной формой записи функции f(x) в виде ряда Фурье, называемого комплексной формой Фурье. Получить эту новую форму помогают известные тождества Эйлера, устанавливающие связь между тригонометрическими функциями и показательными функциями:

Aiα

= cosα +i sinα;

A−iα

= cosα −i sinα.

Отсюда

Aiα + A−iα

Aiα −A−iα

cosα =

;

sinα

С помощью последних формул можно преобразовать

общий член ряда (2.27):

cos nx =

Ainx +A−inx

;

sin nx =

Ainx

−A−inx

= i

A−inx −Ainx

Подставляя вместо cosnx и

sinnx

найденные для них

выражения в формулу (2.27), получим

−A

) =

f (x) = α0 + ∑(αn

inx

−inx

+ibn A

−inx

inx

∞

n=1

0 +

∞

−ib

+ib

∑

n Ainx +

n A−inx .

n=1

Из формул (2.28) вытекает, что если изменить знак n, то αn сохранит свой знак, а bn поменяет его на противоположный. Другими словами, αn – четная, а bn – нечетная функция относительно n:

αn = α−n ; bn = −b−n

Учитывая это, выражение для f(x) можно записать так:

f (x) =	α		∞	α		−ib	−∞	α		−ib
f (x) =		0	+ ∑		n	n Ainx + ∑			n	n Ainx =
	2		n=1			2	n=1			2

+∞	α	n	−ib
= ∑		n	n Ainx .
n=−∞			2

(n = 0, ± 1, ± 2, …).

При n = 0 f (x) = α20 . Обозначая Cn = αn −ibn , окончательно получаем

1 +∞

f (x) = 2 ∑CnAinx .

n=−∞

Коэффициент Cn легко найти, если учесть формулы (2.28) и формулу Эйлера:

Сn = αn −ibn =			1	π∫ f (x)cos nxdx −i					1	π∫ f (x)sin nxdx =
Сn = αn −ibn =			π	π∫ f (x)cos nxdx −i					π	π∫ f (x)sin nxdx =
				−π						−π
=	1	π∫ f (x)(cos nx −i sin nx)dx =					1	π∫ f (x)A−inxdx.
=	π	π∫ f (x)(cos nx −i sin nx)dx =					π	π∫ f (x)A−inxdx.
	π	−π					π	−π
		−π						−π
Таким образом, ряд Фурье в комплексной форме имеет
вид					1	∞
						∞
		f (x)		=		∑CnAinx ,		(2.29)
		f (x)		=		∑CnAinx ,		(2.29)
					2 n=−∞

где комплексный коэффициент (комплексная амплитуда) определяется по формуле

Сn = αn −ibn =			1	π∫ f (x)A−inxdx.	(2.30)
			π
				−π

Для действительной функции f(x) коэффициенты Cn и C-n
являются взаимно сопряженными комплексными числами:
Сn = αn −ibn ,			C−n = αn +ibn .
Замечание. Если f(x) – периодическая функция периода T
= 2l, которая удовлетворяет			условиям разложимости в			ряд
Фурье, то подстановка x =	l	t приводит к функции			lt
					f	с
	π				π

периодом 2π, разложимой в ряд Фурье. Для такой функции по формулам (2.29) и (2.30) имеем:

1 ∞

int

∑CnA

где

2 n=−∞

−int

∫

dt.

−π

Возвращаясь

к аргументу

х,

помощью соотношения

t =

πx получим ряд Фурье функции f(x)

периода T

= 2l в

комплексной форме:

nπ

+∞

f (x) =

∑CnAi

x ,

(2.31)

где

2 n=−∞

nπ

1 π

Сn =

∫f(x)A

−i

x dx =

∫f(x)A−i

xdx.

(2.32)

π l

−l

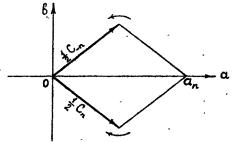
Замечание. Если прибегнуть к комплексной плоскости, то сказанное выше приобретает яркую геометрическую интерпретацию. Можно сказать, что ряд (2.29) содержит два бесконечных ряда сопряженных относительно оси действительных величин векторов, которые вращаются при изменении n в противоположные стороны. Геометрическая сумма каждой пары сопряженных векторов имеет только действительную составляющую αт (рис. 2.11).

Рис. 2.11.

В результате суммирования двух бесконечных рядов сопряженных векторов получается действительная функция f(x). Таким образом, n-й член (n-ая гармоника) ряда Фурье содержит два одинаковых компонента, равных проекции вращающихся сопряженных векторов на ось действительных величин. Амплитуда и фаза n-й гармоники выражается через αn и bn по формулам:

С	n	= α2	+b2	;	tgϕ	n	= αn .
	n	n	n			n	bn
Пример № 11.							bn
Пример № 11.		Разложить			в комплексный ряд Фурье

периодическую функцию f(x) с периодом 2π, определенную следующим образом:

f (x) = −x, (−π < x ≤ π).

Рис. 2.12

Решение. Проверив выполнение условий разложимости в ряд Фурье для функции f(x) (рис. 2.12), переходим к вычислению коэффициентов Фурье по формуле

Сn =

π∫ f (x)A−inxdx = −

xA−inxdx.

−π

Интеграл, стоящий в правой части последнего равенства,

вычисляется по частям:

−inx

Сn = −

∫xA

dx =

−π

−

∫A

dx =

inπ

−π

inπ −π

=	1	(A−inπ + Ainπ )−	1	A−inx	π	=

	in		n2π2
					−π

= in1 2cos nπ − n21π2 (A−inπ + Ainπ )= in2 cos nπ.

2		,		еслиn - четное,


Cn = in		2		(n ≠ 0)
−			,	еслиn - нечетное,
	in

или

			2
	−				,	еслиn - четное,
	−		in		,	еслиn - четное,
Cn	=		in			(n ≠ 0)
		2		,		еслиn - нечетное,
				,		еслиn - нечетное,
	in

Если n = 0, то полученные формулы не дают результата. Поэтому коэффициент C0 надо вычислить отдельно:

С0

π∫ f (x)dx = −

π∫xdx = 0.

−π

Окончательно получим

− x

= ... =

A−4ix −

A−3ix +

A−2ix

−iA−ix +iAix −

A2ix +

A3ix −....

Это равенство имеет место лишь в точках непрерывности функции f(x). В точках разрыва t=kπ, где k – любое нечетное число, сумма ряда равна нулю.

2.2.2. Спектральный анализ периодических функций.

В физике и технике тригонометрические ряды играют важную роль в изучении периодических процессов, как, например, колебательное движение, распространение волн, сила и напряжение переменного тока и тому подобное.

Простейшей периодической функцией является функция вида

y = Asin(ωt +ϕ),

где A, ω и ϕ - постоянные, t - независимая переменная, которая в физике и технике истолковывается как время. Эту функцию называют гармоникой, так как она описывает простейшее колебательное движение, называемое гармоническим. Постоянную А > 0 называют амплитудой

колебания, ωt + ϕ - фазой колебания,			ϕ - начальной фазой, ω
- частотой колебания.
Легко показать, что гармоника имеет период
T =	2π	.
T =		.
Действительно,	ω
Действительно,
				2π
sin(ωt +ϕ) = sin(ωt +ϕ + 2π) = sin ω t +					+ϕ	=
sin(ωt +ϕ) = sin(ωt +ϕ + 2π) = sin ω t +					+ϕ	=
= sin[ω(t +T ) +ϕ],				ω
= sin[ω(t +T ) +ϕ],

что свидетельствует о том, что функция sin(ωt + ϕ ) является периодической с периодом

T = 2ωπ .

Отметим, что движение, характеризующееся уравнением y = α cosωt +bsinωt,

тоже есть гармоническое колебание. В самом деле, положив

α = Asinϕ, b = Acosϕ,

получим

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.2022452.76 Кб2Учебное пособие 511.pdf
#
30.04.2022453.46 Кб13Учебное пособие 512.pdf
#
30.04.2022455.23 Кб1Учебное пособие 513.pdf
#
30.04.2022455.53 Кб4Учебное пособие 514.pdf
#
30.04.2022455.69 Кб7Учебное пособие 515.pdf
#
30.04.2022455.79 Кб4Учебное пособие 516.pdf
#
30.04.2022455.91 Кб6Учебное пособие 517.pdf
#
30.04.2022455.93 Кб5Учебное пособие 518.pdf
#
30.04.2022456.18 Кб29Учебное пособие 519.pdf
#
30.04.2022248.32 Кб4Учебное пособие 52.pdf
#
30.04.2022457.06 Кб4Учебное пособие 520.pdf