
Учебное пособие 516
.pdf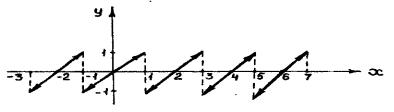
|
|
|
|
|
α0 = |
|
1 |
|
∫2 Axdx = |
1 |
Ax |
2 |
|
= |
|
1 |
(A2 |
−A−2 ), |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
α |
|
= |
1 |
2 |
x |
cos |
nπ |
xdx = |
1 |
|
|
|
|
|
|
|
Ax |
|
|
|
nπ |
sin |
nπx |
+ cos |
nπx |
|
2 |
= |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
n |
|
2 |
−∫2 |
|
|
|
|
l |
|
|
|
|
|
|
|
|
2 |
1 |
|
+ |
|
n2π |
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
− 2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 nπ |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
= |
|
|
|
|
|
|
A |
|
|
|
|
|
sin nπ |
+ cos nπ |
−A |
|
|
|
|
|
|
|
|
sin(−nπ) |
+ |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 2 |
|
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4 + n π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−1)n 2 |
|
2 |
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
+ cos(−nπ) |
|
= |
|
|
|
|
|
|
|
|
|
(A |
|
−A |
|
|
|
), |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 + n |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
nπx |
|
|
|
|
|
nπ(−1) |
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
bn = |
|
|
∫Ax sin |
dx = |
|
|
|
|
(A2 |
|
−A−2 ). |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 + n π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Следовательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
−2 |
|
|
|
1 |
|
|
∞ |
|
|
|
(−1)n 2 |
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
f (x) = |
(A |
|
−A |
|
|
|
) |
|
|
|
+ ∑ |
|
|
|
|
|
|
|
|
cos |
|
|
+ |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 2 |
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
4 + n |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nπ(−1)n+1 |
|
|
|
|
nπx |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + n |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
В точке х = 2 разрыва непрерывности полученный ряд |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сходится к числу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f (2 −0) + f (2 + 0) |
= |
|
A2 −A |
−2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример №5. Разложить функцию
f(x) = x, -1 < x < 1 периода Т = 2 в ряд Фурье (рис. 2.2).
Рис. 2.2.
20
Решение. Функция f(x) – нечетная, удовлетворяющая условиям разложимости в ряд Фурье, поэтому на основании равенств (2.7) и (2.8) имеем:
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = ∑bn sin nπx, |
(здесь l = 1), |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos nπx |
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
bn = 2∫xsin nπxdx = |
2 − x |
|
|
|
|
|
|
|
|
|
0 |
+ |
|
|
∫cos nπxdx |
= |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
nπ |
|
|
|
|
nπ |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
cos nπ |
|
|
|
1 |
|
sin nπx |
|
1 |
|
|
|
|
|
2cos nπ |
|
|
|
|
n+1 |
|
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
= 2 − |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
= |
(−1) |
|
|
|
|
|
. |
|
|||||||||||||
|
|
|
|
|
|
|
n2π2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
nπ |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Следовательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f (x) = |
2 |
|
sinπx |
|
sin 2πx |
|
|
|
sin 3πx |
|
|
|
|
|
|
|
|
|
n+1 sin nπx |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
−... + (−1) |
|
|
|
|
|
|
|
+... |
||||||||||||||||
π |
|
|
1 |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
n |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
или иначе |
|
sinπx |
|
|
sin 2πx |
|
sin 3πx |
|
|
|
|
|
|
|
|
|
|
n+1 sin nπx |
|
|
|
|
|
||||||||||||||||||||||||
x = |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
−... + |
(−1) |
|
|
|
|
|
|
|
|
+... |
, |
||||||||||||
|
π |
|
|
|
1 |
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
n |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где , -1 < x < 1, |
|
Т = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2.1.3. Разложение в ряд Фурье непериодических функций на интервалах ( -l, l ), ( 0, l ), ( α, b ).
1. Разложение в ряд Фурье функций, заданных на интервале ( -l, l ). Кусочно-гладкую непериодическую функцию f(x), заданную на бесконечной оси -∞ < x < ∞, нельзя представить ее рядом Фурье, так как сумма его, будучи суммой гармоник с общим периодом Т, есть функция периодическая с тем же периодом Т, и, следовательно, не может быть равна функции f(x) для всех х. Однако, можно построить представление этой функции в виде
21

соответствующего ряда Фурье на любом конечном промежутке.
Рис. 2.3.
Пусть интересующий нас промежуток есть интервал ( -l , l), симметричный относительно начала координат.
Построим функцию φ(х) периода Т = 2l такую, что
(рис. 2.3)
φ (х) = f (x) при – l < x < l.
Предполагая, что функция φ(х) удовлетворяет условиям разложимости в ряд Фурье, имеем
|
α |
|
|
∞ |
|
|
nπx |
|
|
|
|
nπx |
|
||||||
ϕ(x) = |
|
0 |
+ ∑ αn cos |
|
|
|
+bn sin |
|
|
|
, |
-∞ < x < ∞ (2.10) |
|||||||
|
|
l |
|
l |
|||||||||||||||
где |
2 |
n=1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
nπx |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
αn |
|
1 l |
|
cos |
|
|
|
|
|
|
|
||||
|
|
|
|
|
l |
|
|
|
|
|
|||||||||
|
|
|
|
|
= |
|
∫ϕ |
(x) |
|
|
dx |
|
|
(2.11) |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
bn |
|
l |
−l |
|
sin |
nπx |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(n = 0,1,2,…). |
|
|
|
|
|
|
|
l |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отсюда на основании тождества (2.9) получаем |
|||||||||||||||||||
|
α |
|
∞ |
|
|
|
|
nπx |
|
|
|
|
|
nπx |
|
||||
f (x) = |
|
|
0 |
+ ∑ αn cos |
|
|
|
+bn sin |
|
|
|
, |
(2.10’) |
||||||
|
|
|
l |
|
l |
|
|||||||||||||
|
2 |
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
- l < x < l
где
22

αn |
1 l |
||
b |
= |
|
∫ |
l |
|||
n |
|
|
−l |
cos nπx
f (x) l dx , (2.11’)sin nπx
l
(n = 0,1,2,…).
В силу того, что заданную функцию f(x) нужно представить рядом Фурье лишь на интервале ( - l, l ),
поведение полученного |
ряда |
в точках - |
l и |
l нас |
не |
интересует. |
|
|
|
|
|
2. Разложение в |
ряд |
Фурье функций, |
заданных |
на |
|
интервале (0, l). |
|
|
|
|
|
Пусть теперь непериодическую функцию f(x) требуется |
|||||
представить рядом Фурье периода Т = 2l |
на «полупериоде» |
||||
0 < x < l. |
|
|
|
|
|
Полагая («произвольное продолжение») |
|
|
|
||
f |
(x), 0 < x < l, |
|
(2.12) |
||
ϕ(x) = |
(x), - l < x < 0, |
|
|||
f1 |
|
|
|
||
где f1(x) – произвольная кусочно-гладкая функция, из формул (2.10) и (2.11) получаем бесконечное множество рядов Фурье
f (x) = α20 + ∑∞ (αn cos nπl x +bn sin nπl x ), (2.13)
n=1
( 0 < x < l ),
дающих представление функции f(x) на интервале ( 0, l ). В частности, полагая в (2.12) («четное продолжение»)
f1 (x) = f (−x), (-l < x < 0).
будем иметь
f (x) = α20 + ∑∞ αn cos nπl x , (0 < x < l), (2.14)
n=1
где
|
2 l |
nπx |
|
|
|
αn = |
|
f (x) cos |
|
dx, |
(2.15) |
|
|
||||
|
l |
∫0 |
l |
|
|
(n = 0,1,2,…).
23
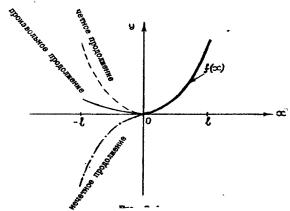
Итак, в этом случае получается разложение функций в ряд только по косинусам.
Аналогично, полагая в (2.12) («нечетное продолжение»)
f1 (x) = − f (−x), (-l < x < 0).
получим
|
|
|
|
∞ |
|
|
nπx |
|
|
|
|
|
f (x) = ∑bn sin |
, |
(2.16) |
||||
|
|
l |
|||||||
|
|
|
|
n=1 |
|
|
|
|
|
где |
|
( 0 < x < l ), |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 l |
nπx |
|
|
|
|
|
b |
= |
|
|
f (x)sin |
|
dx, |
|
(2.17) |
|
|
|
|
|
||||||
n |
|
|
l |
∫0 |
l |
|
|
|
|
|
|
|
|
|
|
|
|||
(n = 0,1,2,…).
В этом случае получается разложение функции в ряд только по синусам.
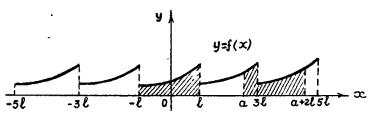
Таким образом, если функция задана в интервале ( 0 < x < l ), то, продолжая ее на интервале - l < x < 0, а затем продолжая полученную функцию периодически на всю числовую прямую, мы можем получить бесчисленное множество рядов Фурье. Однако все эти ряды на интервале (0, l) будут представлять одну и туже заданную функцию f(x), а на интервале ( - l, 0 ) каждый ряд будет иметь своей суммой соответствующее продолжение функции f(x) (рис. 2.4).
Рис. 2.4
24
3. Разложение в ряд Фурье функций, заданных на интервале ( α, b ). Прежде чем рассматривать этот вопрос, сделаем следующее утверждение.
Утверждение. Интеграл от периодической функции f(x) по любому отрезку, длина которого равна периоду T = 2l, имеет всегда одно и то же значение, т.е.
l |
α +2l |
|
|
∫ f (x)dx = |
∫ |
f (x)dx, |
(2.18) |
−l |
α |
|
|
где α – любое вещественное число.
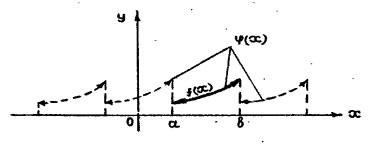
Действительно, основываясь на геометрическом смысле определенного интеграла, справедливость формулы (2.18) легко проиллюстрировать: площади, заштрихованные на рисунке 2.5., равны между собой.
Рис. 2.5.
Замечание. Из данного утверждения следует, что при вычислении коэффициента Фурье, мы можем заменить промежуток интегрирования [ -l, l ], любым промежутком [ α, α + 2l ], длина которого равна T = 2l, то есть положить
αn |
= |
1α +2l |
f (x) cos |
|
nπx |
dx, (n = 0,1,2,…). |
(2.19) |
||||
|
|
|
|
|
|
||||||
|
l α∫ |
|
l |
||||||||
|
|
|
|
|
|
|
|
||||
b |
= |
|
1α +2l |
f (x)sin |
nπx |
dx, |
(n = 0,1,2,…). |
(2.20) |
|||
|
|
|
|
|
|
||||||
|
l α∫ |
|
|
|
|||||||
n |
|
|
|
|
l |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
где α –любое вещественное число, |
T = 2l – период функции |
||||||||||
f(x). |
|
|
|
|
|
|
|
|
|
|
|
Пусть теперь на некотором интервале (α, b) задана непериодическая функция f(x), удовлетворяющая условиям
25
разложимости в ряд Фурье. Введем в рассмотрение вспомогательную периодическую функцию φ(х) с периодом Т = b – α = 2l, совпадающую с функцией f(x) на интервале (α, b)
(рис. 2.6)
Рис. 2.6.
Разложим периодическую функцию φ(х) в ряд Фурье. Сумма этого ряда во всех точках интервала (α, b) (кроме точек разрыва) совпадает с заданной функцией f(x), то есть ием самым имеем разложение функции f(x) в ряд Фурье на
интервале (α, b), |
(Т = b – α = 2l , b = α + 2l, l = |
b −α |
): |
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
α0 |
∞ |
|
|
|
2nπx |
|
|
|
|
|
2nπx |
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f (x) = |
+ ∑(αn cos |
+bn sin |
|
), (α < x < b), |
(2.21) |
|||||||||||||||||||||||||
b −α |
|
|
|
|||||||||||||||||||||||||||
где |
|
|
|
|
2 |
n=1 |
|
|
|
|
|
|
|
b −α |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
α + 2l |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
nπx |
|
|
|
2 |
|
|
|
|
|
|
|
2nπx |
|
|
|
||||||||||
αn |
= |
|
|
|
α∫ |
f (x) cos |
|
|
|
dx |
= |
|
|
|
|
|
α∫ |
f (x) cos |
|
|
|
|
dx, |
(2.22) |
||||||
|
l |
|
l |
b − |
α |
|
b − α |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(n = 0,1,2,…). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
b |
= |
1α+2l |
f (x)sin |
nπx |
dx = |
|
2 b |
f |
(x)sin |
2nπx |
dx, |
|
|
(2.23) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
l α∫ |
|
|
b −α α∫ |
|
|
|
|
|||||||||||||||||||||||
n |
|
|
l |
|
|
|
|
|
|
|
|
|
|
b −α |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(n = 1,2,…).
Замечание. Полагая в формулах (2.21) – (2.23) α = 0 и b = l, можно получить еще одно представление в виде полного ряда Фурье непериодической функции f(x), заданной на интервале (0, l):
26
|
|
|
|
|
α0 |
∞ |
|
|
|
|
2nπx |
|
2nπx |
|
|
f (x) = |
+ ∑(αn cos |
+bn sin |
), (0 < x < l), (2.24) |
||||||||||||
l |
|
||||||||||||||
где |
|
|
|
|
2 |
n=1 |
|
|
|
|
|
l |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 l |
|
|
2nπx |
|
|
|
|
|||||
αn = |
|
|
|
f |
(x) cos |
|
|
|
dx, |
|
(2.25) |
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
l |
∫0 |
|
|
l |
|
|
|
|
|
|
||
(n = 0,1,2,…) |
|
|
|
|
|
|
|
|
|||||||
|
|
2 l |
|
2nπx |
|
|
|
|
|
|
|||||
b |
= |
|
|
|
f (x)sin |
|
|
dx, |
|
(2.26) |
|||||
|
|
|
|
|
|
||||||||||
n |
|
l ∫0 |
|
|
l |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
(n = 1,2,…).
Замечание. Полагая l = π, из формул (2.9) – (2.26) легко получить соответствующие результаты для частного случая непериодических функций, заданных на интервале (-π, π), (0, π) и (α, α+2π).
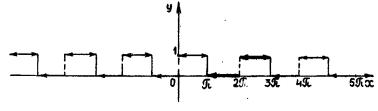
Пример № 6. Разложить в ряд Фурье функцию f(x), определенную следующим образом
0, при π < x ≤ 2π f (x) =
1, при 2π < x < 3π
Решение. Здесь функция f(x) задана на интервале (α, b) длиной 2π. Периодически продолжим заданную функцию на всю числовую ось, получим периодическую функцию периода
2π (рис. 2.7).
Рис. 2.7.
27
Полагая в формулах (2.22) – (2.23) α = π, b = 3π, l = π, вычислим коэффициент Фурье данной функции:
|
|
|
|
1 |
|
3π |
|
|
|
|
1 |
2π |
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
α0 = |
|
|
∫ |
f (x)dx = |
∫0dx + |
1 |
∫1dx =1; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
π |
π |
π |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
π |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 3π |
|
|
|
|
|
|
|
|
|
1 3π |
|
|
|
1 sin nx |
|
3π |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
αn = |
|
|
|
|
π∫ |
f (x) cos nxdx = |
|
|
2∫πcos nxdx + |
|
|
|
|
|
|
|
|
|
|
|
|
2π |
= 0; |
|||||||||||||||||||
π |
π |
π |
|
n |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
1 3π |
|
|
|
|
|
|
|
|
1 3π |
|
|
1 cos nx |
|
3π |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
bn = |
|
|
|
π∫ |
f (x)sin nxdx = |
|
2∫πsin nxdx + |
|
|
|
|
|
|
|
2π |
= |
||||||||||||||||||||||||||
|
π |
π |
π |
|
n |
|
|
|||||||||||||||||||||||||||||||||||
= − |
|
1 |
[(−1)n −1]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
πn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Запишем ряд Фурье функции f(x): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
f (x) = |
1 |
+ |
2 |
( |
sin x |
+ |
sin 3x |
+ |
sin 5x |
+ |
sin 7x |
+...). |
|
|||||||||||||||||||||||||||||
|
π |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
2 |
|
1 |
|
|
3 |
|
|
|
|
|
5 |
7 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
В точке разрыва x = 2π полученный ряд будет сходиться к среднему арифметическому предельных значений функции
f(x) справа и слева, т.е. к числу 12 .
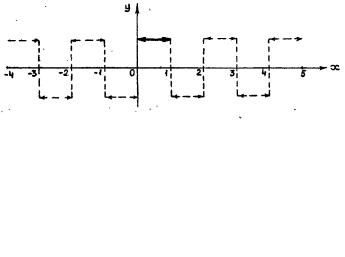
Пример № 7. Разложить функцию f(x) = 1 , заданную в интервале 0 < x <1, в ряд по синусам.
Решение. Для разложения функции f(x) в ряд по синусам надо ее продолжить на интервал –1 < x < 0 нечетным образом, а затем продолжить полученную функцию периодически на всю числовую ось (рис. 2.8).
Рис. 2.8.
28
Для решения задачи нам необходимо воспользоваться формулами (2.16) и (2.17), где надо принять l = 1, f(x) = 1. Тогда
b |
|
|
|
|
|
|
|
2 l |
f (x)sin |
|
nπx |
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= |
|
|
|
|
|
|
|
|
|
|
dx |
= |
|
|
|
1sin nπxdx = |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
l |
∫0 |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
1 ∫0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= −2 |
cos nπx |
|
1 = − |
2 |
[cos nπ |
−cos0]= − |
2 |
|
|
[(−1)n −1]. . |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
nπ |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
0 |
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|||||||
b = |
, |
|
b = 0, |
|
b = |
|
, |
b = 0, |
b = |
|
, … . |
|
|
|||||||||||||||||||||||||||
|
π |
|
|
3π |
5π |
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
5 |
|
|
|
|
|
|||||||||||||||
Ряд Фурье для данной функции имеет вид |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
4 sin x |
|
|
sin 3x |
|
sin 5x |
|
|
|
|
|
|
sin(2n −1) |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
+... |
+ |
|
|
|
|
+ |
... |
= |
|
|
|||||
|
π |
|
|
1 |
|
|
3 |
|
|
|
5 |
|
|
|
2n |
−1 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
4 |
|
|
|
|
∞ |
|
sin(2n −1)x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
∑ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
π |
n=1 |
|
2n −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример №8. |
Разложить |
|
|
функцию |
|
|
|
f (x) = x − |
x2 |
, |
||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
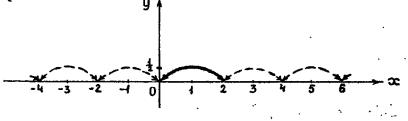
заданную в интервале 0 < x <2, в ряд по косинусам.
Решение. Для разложения данной функции f(x) в ряд по косинусам надо ее продолжить на интервал –2 < x < 0 четным образом, а затем продолжить полученную функцию периодически на всю числовую ось (рис. 2.9).
Рис. 2.9.
29
