
Учебное пособие 516
.pdf
α0 = |
1 |
|
π∫ f (x)dx = |
2 |
π∫ f (x)dx, |
|||||
π |
π |
|||||||||
|
|
|
|
|
|
−π |
0 |
|
|
|
αn = |
1 |
|
π∫ f (x)dx cos nxdx = |
2 |
π∫ f (x) cos nxdx, |
|||||
π |
|
π |
||||||||
|
|
|
|
|
|
−π |
0 |
|||
bn = |
1 |
|
|
π∫ f (x) sin nxdx = 0. |
||||||
π |
|
|||||||||
|
|
|
|
|
−π |
|
|
|
|
|
Таким образом, ряд Фурье для четной функции содержит только четные функции – косинусы, а записывается так:
f (x) = α0 + ∑∞ αn cos nx, (1.14)
2 n=1
при этом
α0 = |
2 |
π∫ f (x)dx, |
(1.15) |
π |
|||
0 |
|
||
αn = 2 π∫ f (x) cos nxdx. (1.16)
π0
2.Пусть f(x) – нечетная периодическая функция с
периодом 2π, удовлетворяющая условиям разложимости в ряд Фурье. Тогда рассуждая аналогично, получим
α0 = |
1 |
|
|
π∫ f (x)dx = 0, |
|
|
||
π |
|
|
||||||
|
|
|
|
|
|
−π |
|
|
αn = |
1 |
|
|
π∫ f (x) cos nxdx = 0, |
||||
π |
|
|||||||
|
|
|
|
|
|
−π |
|
|
bn = |
1 |
|
|
π∫ f (x) sin nxdx = |
2 |
π∫ f (x) sin nxdx. |
||
π |
|
|
π |
|||||
|
|
|
|
|
|
−π |
0 |
|
Таким образом, ряд Фурье для нечетной функции содержит только нечетные функции – синусы, и записывается следующим образом:
∞ |
|
f (x) = ∑bn sin nx, |
(1.17) |
n=1
10
при этом
bn = |
2 |
π∫ f (x) sin nxdx. |
(1.18) |
π |
|||
0 |
|
||
Замечание. Отметим, что важным свойством четных и нечетных функций, как показывают формулы (1.15), (1.16) и (1.18), является то, что для определения коэффициентов Фурье достаточно пользоваться функцией f(x), заданной на половине периода.
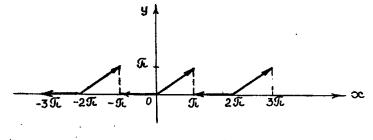
Пример 1. Разложить в ряд Фурье функцию
x, 0 ≤ x ≤ π, f (x) = 0, −π < x < 0,
удовлетворяющую условию f(x+2π)=f(x) (рис.1.1).
Рис. 1.1.
Решение. Функция f(x) удовлетворяет условиям разложимости в ряд Фурье, поэтому можно записать:
|
|
|
α0 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
+ ∑(αn cos nx +bn sin nx), |
|
|
|
||||||||||||
|
|
|
2 |
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
при этом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 π |
|
1 0 |
|
1 |
π |
|
1 x2 |
|
π |
|
π |
|
|||||
|
|
|
|
|
|
|
||||||||||||
α0 = |
|
−∫π f (x)dx = |
|
−∫π |
0dx + |
|
∫0 |
xdx = 0 + |
|
|
|
|
|
0 |
= |
|
, |
|
π |
π |
π |
π |
|
2 |
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
11
αn = |
1 |
π∫ f (x) cos nxdx = |
1 |
π∫x cos nxdx = |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
π |
π |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
xsin nx |
|
π |
|
|
|
|
|
1 |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos nx |
|
π |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
∫0 |
sin nxdx = |
|
|
|
|
|
|
|
|
= |
|
|
|||||||||||||||||||||
π |
|
|
n |
|
|
|
0 |
|
n |
|
n2π |
|
|
|
0 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
при |
n - четном, |
||||||||||||||||||||||||||
|
cos nπ −1 |
|
|
|
|
|
|
(−1) |
n |
−1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
= |
= |
|
|
|
|
= |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
n2π |
|
|
|
|
|
|
|
|
|
|
n2π |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
, |
|
при |
n - нечетномм |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n π |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
при n - четном, |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
αn |
= |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
, |
|
при |
n - нечетном |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
bn = |
1 |
|
π∫ f (x)sin nxdx = |
1 |
π∫xsin nxdx = |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
π |
π |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
x cos nx |
|
π |
|
|
1 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= |
|
|
− |
|
|
|
|
|
|
|
|
|
|
0 |
+ |
|
|
|
|
∫0 |
cos nxdx |
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
π |
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
(−1)n+1 |
|
||||||||||||||||||||
|
1 |
|
|
x cos nx |
|
|
|
|
|
|
sin nx |
|
|
|
|
|
|
cos nπ |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
= |
|
|
− |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
= |
|
|
|
, |
|||||||||||||||
π |
|
n |
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
0 |
|
|
|
|
|
n |
|
|
n |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
b |
= |
|
(−1)n+1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
f (x) = |
π + (− |
2 |
cos x +sin x) − |
sin 2x |
|
+ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
12
+(−92π cos3x + 13 sin 3x) − sin44x +
+(− 252π cos5x + 15 sin 5x) +...
Полагая в этом равенстве х = 0, получим
0 = π4 − π2 (1 + 312 + 512 +...),
откуда
∑ 1 |
2 |
= |
π |
2 |
. |
|
∞ |
|
|
|
|
|
|
n=1 (2n −1) |
|
|
8 |
|
||
Используя этот результат, нетрудно убедиться в том, что сумма ряда, записанного в правой части равенства (1.19), при х = π (а следовательно, и при х = (2k+1) π, k – любое целое число), равна π / 2, то есть равна
f (π −0) + f (π + 0) . 2
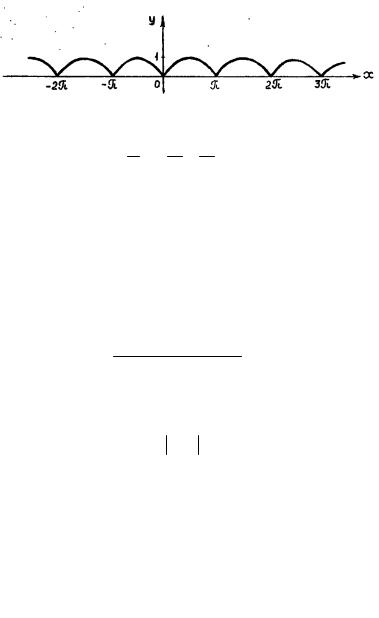
Пример № 2. Разложить в ряд Фурье функцию
f (x) = sin x ,
удовлетворяющую условию f(x+2 π)=f(x) (рис. 1.2.)
Рис. 1.2
13
Решение. Функция f(x) удовлетворяет условию разложимости в ряд Фурье и является четной функцией, поэтому в разложении ее в ряд Фурье отсутствуют синусы, т.е.
bn = 0.
Тогда
|
2 |
π |
4 |
|
α0 = |
|
∫sin xdx = |
|
, |
π |
π |
|||
|
|
0 |
|
|
αn = |
2 |
|
π∫sin x cos nxdx = |
1 |
π∫[sin(n +1)x −sin(n −1)x]dx = |
||||||||||||||||||||||||||||||||||||||||
π |
π |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
cos(n +1)x |
|
π |
|
|
|
cos(n −1)x |
|
π |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
− |
|
|
|
|
|
|
|
|
|
|
|
0 |
= |
|
|
|
|
|
||||||||
π |
|
|
|
n +1 |
|
|
|
|
|
|
|
|
n −1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= − |
1 |
(−1)n+1 −1 |
− |
(−1)n−1 −1 |
= −2 |
|
(−1)n +1 |
, |
если n ≠ 1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
π |
|
|
|
n +1 |
|
|
|
|
n −1 |
|
π(n |
2 |
−1) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
еслиn = 3,5,7... |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αn = |
− |
|
|
|
|
|
|
|
|
|
|
, |
еслиn = 2,4,6,... |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π(n |
2 |
−1) |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
При n = 1 находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
α1 |
= |
|
2 |
π∫sin x cos xdx = |
1 |
π∫sin 2xdx = 0. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
π |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
Окончательно получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
sin x |
|
|
|
|
2 |
|
4 |
|
cos 2x |
|
|
|
cos 4x |
|
cos6x |
|
|
|
|
|||||||||||||||||||||||||
|
= |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+... . |
|
|
|||||||||
|
π |
π |
|
|
|
3 |
|
|
|
15 |
|
35 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Так как функция непрерывна, это равенство выполняется во всех точках.
14
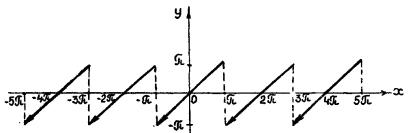
Пример №3. Разложить в ряд Фурье периодическую функция f(x) с периодом 2π, определенную следующим образом (рис. 1.3):
f (x) = x, - π < x ≤ π,
Рис. 1.3.
Решение. Функция f(x) удовлетворяет условиям разложимости в ряд Фурье и является нечетной функцией, поэтому ее ряд Фурье будет содержать только синусы, то есть
α0=0, αn=0.
Интегрируя по частям, вычислим коэффициенты:
|
2 π |
2 |
|
|
x cos nx |
|
π |
1 |
π |
|
|
|||
|
|
|
||||||||||||
|
|
∫x sin nxdx = |
|
|
|
|
|
|
|
|
|
|
|
|
bn = π |
π |
|
− |
n |
|
0 |
+ n |
∫cos nxdx |
= |
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= − |
2 cos nπ |
|
= (−1)n+1 |
2 |
, n =1,2,3,4,... . |
|
|||||||
|
n |
|
n |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, получаем ряд |
|
|
|
||||||||||
x = |
sin x |
|
|
sin 2x |
|
sin 3x |
|
n+1 sin nx |
|
||||
2 |
|
|
− |
|
+ |
|
|
−... + (−1) |
|
|
+... . |
||
|
2 |
|
3 |
|
n |
||||||||
|
1 |
|
|
|
|
|
|
|
|||||
Это равенство имеет место лишь в точках непрерывности функции f(x). В точках разрыва x = kπ, где k – любое нечетное число, сумма ряда равна среднему арифметическому ее пределов справа и слева, т.е. нулю. Действительно, для k = 1
15

lim f (x) = f (π −0) =π
x→π−0
lim f (x) = f (π + 0) =π ,
x→π +0
f (π −0) + f (π + 0) = 0. 2
Аналогично и в остальных точках разрыва.
2. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ЛЮБЫМ
ПЕРИОДОМ.
2.1.1. Ряды Фурье для функций с любым периодом
Пусть f(x) – периодическая функция произвольного периода Т = 2l (l – полупериод), кусочно-монотонная или кусочно-гладкая на отрезке [ -l, l ]. Полагая х = αt, получим функцию f(αt) аргумента t, период которой равен 2l / α.
Подберем α так, чтобы период функции f(αt) был равен
2π, т.е.
αT = 2αl = 2π, откуда α = πl .
Тогда подстановка x = πl t (сжатие или растяжение по оси ОХ) приводит к функции
f πlt периода 2π.
Эта функция удовлетворяет условию разложимости в ряд Фурье, так как она кусочно-гладкая или кусочно-монотонная на отрезке [ -π; π]. (Нетрудно заметить, что отрезку [ -l, l ] значения х соответствует отрезок [ -π; π] значений t).
|
|
|
|
lt |
|||
Разлагая функцию |
f |
|
|
||||
π |
|||||||
|
|
|
|
|
|||
lt |
|
α |
|
||||
f |
|
|
= |
|
|
0 |
|
|
|
|
|||||
|
π |
|
|
2 |
|||
в ряд Фурье, получим:
∞
+ ∑(αn cos nt +bn sin nt),
n=1
16
при этом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
π lt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
α0 |
|
= |
|
|
|
|
|
f |
|
|
|
|
dt, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
π |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−∫π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
π lt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
αn |
= |
|
|
|
|
|
|
|
|
|
|
cos ntdt, |
|
|
|
|
|
|
|
|
|
|
|
(2.2) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
π −∫π π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
π lt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
bn |
= |
|
|
|
|
|
f |
|
|
|
|
sin ntdt, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−∫π π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Исходя |
из |
равенства |
|
|
|
x = |
|
l |
|
t, перейдем теперь |
снова к |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
переменной х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
π x, |
|
|
|
|
|
|
|
π dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Так как |
t = |
|
dt = |
|
|
и пределы интегрирования |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по t от –π до π |
|
соответствуют пределы по х от –l до |
l, то ряд |
||||||||||||||||||||||||||||||||||||||||
Фурье функции f(x) периода Т = 2l запишется в виде: |
|
||||||||||||||||||||||||||||||||||||||||||
|
α |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|||||||||||
f (x) = |
|
0 = ∑ αn cos |
|
|
|
|
x +bn sin |
|
|
|
|
|
|
x , |
|
|
(2.3) |
||||||||||||||||||||||||||
|
|
|
l |
|
l |
|
|
||||||||||||||||||||||||||||||||||||
при этом |
2 |
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
1 |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
α0 = |
|
* πl −∫l f (x)dx = |
−∫l f (x)dx, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
π |
l |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
π l |
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
1 l |
|
|
nπ |
|
||||||||||||||||
αn |
= |
|
|
|
|
* |
l −∫l f (x)cos |
|
|
|
xdx = |
|
|
−∫l f (x)cos |
|
|
xdx, |
||||||||||||||||||||||||||
|
|
π |
|
l |
|
l |
l |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
π l |
|
|
|
|
|
|
|
|
nπ |
|
|
1 l |
|
nπ |
|
|
|
|||||||||||||||||
bn |
= |
|
* |
l −∫l f (x)sin |
|
|
|
xdx = |
|
−∫l f (x)sin |
|
xdx, |
|||||||||||||||||||||||||||||||
π |
|
l |
l |
l |
|||||||||||||||||||||||||||||||||||||||
Определение. Рядом Фурье функции f(x) произвольного периода Т = 2l, интегрируемой на отрезке [-l, l], называется тригонометрический ряд типа
α0 |
∞ |
nπ |
|
nπ |
|
|
|
+ ∑(αn cos |
x +bn sin |
x), |
(2.3’) |
||||
l |
|
||||||
2 |
n=1 |
|
l |
|
|||
коэффициенты которого определяются равенствами
17

|
|
1 |
l |
|
|
|
|
|
|
|
|||||
α0 |
= |
−∫l |
f (x)dx, |
|
|
||||||||||
|
|
l |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
l |
|
|
nπ |
|
|
|
||||||
αn |
= |
−∫l |
f (x)cos |
xdx, |
|
(2.4) |
|||||||||
|
l |
|
|
|
|||||||||||
|
|
|
|
|
l |
|
|
||||||||
|
|
1 |
|
l |
|
nπ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
bn |
= |
|
f (x)sin |
xdx, |
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
|
|
l −∫l |
|
|
l |
|
|
||||||||
Если f(x) – функция периода T=2l кусочно-монотонная или кусочно-гладкая на отрезке [ -l, l ], то она разлагается в ряд Фурье, т.е. равенство (2.3) справедливо во всех точках непрерывности функции f(x).
В точках х0 разрыва функции f(x) сумма ряда (2.3’) равна
f (x0 −0)+ f (x0 + 0). 2
2.1.2. Ряды Фурье для четных и нечетных функций с любым периодом.
1. Пусть f(x) – четная, кусочно-монотонная или кусочногладкая периодическая с Т = 2l функция, тогда ее можно разложить в ряд Фурье. По свойству интеграла, по симметричному относительно х = 0 интервалу, получим bn = 0, а также
|
|
|
l |
∫0 |
|
|
|
||
α0 |
= |
2 |
l |
f (x)dx, |
|
(2.5) |
|||
|
|
|
|
||||||
αn |
= |
2 l |
f (x)cos |
nπ |
xdx, |
||||
|
|
|
|
|
|||||
l ∫0 |
l |
||||||||
|
|
|
|
||||||
Таким образом, ряд Фурье четной функции f(x) периода Т = 2l запишется в виде:
|
α0 |
∞ |
nπ |
|
|
|
f (x) = |
+ ∑αn cos |
x, |
(2.6) |
|||
|
||||||
|
2 |
n=1 |
l |
|
||
при этом коэффициенты ряда определяются равенствами (2.5).
18
2. Пусть f(x) – нечетная кусочно-монотонная или кусочногладкая периодическая с Т = 2l функция, тогда по свойству интеграла, по симметричному относительно х = 0 интервалу, получим α0 =0 αn = 0, а также
|
2 l |
|
nπ |
|
|
|
b = |
|
∫0 |
f (x)sin |
|
xdx, |
(2.7) |
|
|
|||||
n |
l |
|
l |
|
|
|
|
|
|
|
|||
Таким образом, ряд Фурье нечетной функции f(x) периода Т = 2l запишется в виде
∞ |
nπ |
|
|
|
f (x) = ∑bn sin |
x, |
(2.8) |
||
|
||||
n=1 |
l |
|
||
при этом коэффициенты ряда определяются равенством (2.7).
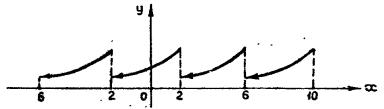
Пример № 4. Разложить функцию f (x) = Ax , − 2 < x ≤ 2
периода Т = 2l = 4 в ряд Фурье (рис. 2.1).
Рис. 2.1.
Решение. Данная функция удовлетворяет условиям разложимости в ряд Фурье, поэтому на основании равенств
(2.3) и (2.4) имеем:
|
α0 |
∞ |
nπ |
|
nπ |
|
|
f (x) = |
+ ∑(αn cos |
x +bn sin |
x), |
||||
l |
|
||||||
|
2 |
n=1 |
2 |
|
|||
где
19
