
Методическое пособие 447
.pdf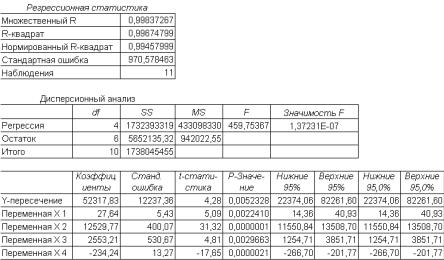
Рис. 12. Результаты расчетов
Витоге мы получили следующую математическую
модель:
y = 52318 + 27,64*x1 + 12530*x2 + 2553*x3 - 234,24*x4. (27)
Теперь застройщик может определить оценочную стоимость здания под офис в том же районе. Если это здание имеет площадь 2500 квадратных метров, три офиса, два входа и время эксплуатации - 25 лет, можно оценить его стоимость, используя следующую формулу:
y = 27,64*2500 + 12530*3 + 2553*2 - 234,24*25 + 52318=
=158 261 у.е.
Врегрессионном анализе наиболее важными результатами являются:
коэффициенты при переменных и Y-пересечение, являющиеся искомыми параметрами модели;
множественный R, характеризующий точность модели для имеющихся исходных данных;
F-критерий Фишера [10] (в рассмотренном примере он значительно превосходит критическое значение, равное
4,06);
39
t-статистика [10] – величины, характеризующие степень значимости отдельных коэффициентов модели.
На t-статистике следует остановиться особо. Очень часто при построении регрессионной модели неизвестно, влияет тот или иной фактор x на y. Включение в модель факторов, которые не влияют на выходную величину, ухудшает качество модели. Вычисление t-статистики помогает обнаружить такие факторы. Приближенную оценку можно сделать так: если при n>>k величина t-статистики по абсолютному значению существенно больше трех, соответствующий коэффициент следует считать значимым, а фактор включить в модель, иначе исключить из модели. Таким образом, можно предложить технологию построения регрессионной модели, состоящую из двух этапов:
1)обработать пакетом "Регрессия" все имеющиеся данные, проанализировать значения t-статистики;
2)удалить из таблицы исходных данных столбцы с теми факторами, для которых коэффициенты незначимы и обработать пакетом "Регрессия" новую таблицу.
Для примера рассмотрим переменную x4. В справочнике по математической статистике t-критическое с (n-k-1)=6 степенями свободы и доверительной вероятностью 0,95 равно 1,94. Поскольку абсолютная величина t, равная 17,7 больше, чем 1,94, срок эксплуатации - это важная переменная для оценки стоимости здания под офис. Аналогичным образом можно протестировать все другие переменные на статистическую значимость. Ниже приводятся наблюдаемые t- значения для каждой из независимых переменных, представленных в табл. 8:
Таблица 8
Наблюдаемые t-значения
Общая площадь |
5,1 |
Количество офисов |
31,3 |
Количество входов |
4,8 |
Срок эксплуатации |
17,7 |
40
Все эти значения имеют абсолютную величину большую, чем 1,94; следовательно, все переменные, использованные в уравнении регрессии, полезны для предсказания оценочной стоимости здания под офис в данном районе.
Задания:
1. Построить зависимость количества выигранных голов от характеристик сыгранных игр на основе модели множественной регрессии.
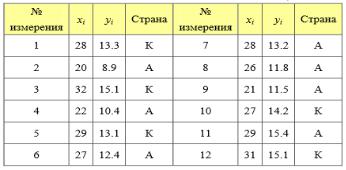
2.Построить регрессионную модель и вычислить оценки для ее коэффициентов для исследования влияния на вес куриных окорочков ( переменная Y ) возраста куры ( переменная X ) и страны происхождения куры ( Америка, Канада ) по данным таблицы, показанной на рис. 13.
Рис. 13. Входные данные
Проверить значимость построенной регрессии и коэффициентов регрессии
Рекомендация. Введите в модель фиктивную переменную z, равную 1, если куры из Канады; 0, если куры из Америки.
3. С целью исследования влияния факторов 1– среднемесячного количества профилактических наладок автоматической линии и 2 – среднемесячного числа обрывов
41
нити на показатель y – среднемесячную характеристику качества ткани ( в баллах ) по данным 37 предприятий легкой промышленности были вычислены парные коэффициенты корреляции: 1= 0.105, 2= 0.024 и 12 1 2= 0.996.
Определить частные коэффициенты корреляции 1( 2) и2( 1) и оценить их значимость на уровне 0.05.
Контрольные вопросы:
1.Для каких целей используется регрессионный
анализ?
2.Что такое уравнение регрессии?
3.Какие типы регрессии существуют?
4.Что такое F – критерий Фишера?
5.Что такое t- статистика?
6.Что такое коэффициент детерминации?
7.Каким образом определяется коэффициент множественной корреляции Пирсона?
42
Практическое занятие № 7 Дисперсионный анализ результатов моделирования
Цель работы: Рассмотреть основные понятия и математический аппарат дисперсионного анализа результатов моделирования, получить практические навыки по решению задач.
Теоретические сведения
При обработке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных {y(1)}, {y(2)}, …, {y(n)} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моментов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах исследуемой модели ММ, а следовательно, и системы S. Попарное использование для этих целей критериев Смирнова и Стьюдента для проверки нулевой гипотезы затруднено в связи с наличием большого числа выборок при моделировании системы. Поэтому для этой цели используется дисперсионный анализ [11].
Пример: Рассмотрим решение задачи дисперсионного анализа при обработке результатов моделирования системы в следующей постановке. Пусть генеральные совокупности случайной величины {у(1)}, {y(2)}, ..., {y(n)} имеют нормальное распределение и одинаковую дисперсию. Необходимо по выборочным средним значениям при некотором уровне значимости γ проверять нулевую гипотезу H0 о равенстве математических ожиданий. Выявим влияние на результаты моделирования только одного фактора, т.е. рассмотрим однофакторный дисперсионный анализ.
43
Допустим, изучаемый фактор x привел к выборке значений неслучайной величины Y следующего вида: y1, y2, ..., yk, где k – количество уровней х. Влияние фактора будем оценивать неслучайной величиной Dx, называемой факторной дисперсией [11]:
|
|
|
̅̅̅2 |
|
|
|
= 2 |
= ∑ |
( − ) |
. |
(28) |
|
|||||
|
|
=1 |
|
|
|
|
|
|
|
||
где y – среднее арифметическое значение величины Y.
Если генеральная дисперсия D[y] известна, то для оценки случайности разброса наблюдений необходимо сравнить D[y] с выборочной дисперсией Sв2, используя критерий Фишера (F-распределение). Если эмпирическое значение Fэ попадает в критическую область, то влияние фактора х считается значимым, а разброс значений х – неслучайным. Если генеральная дисперсия D[x] до проведения машинного эксперимента с моделью ММ неизвестна, то необходимо при моделировании найти ее оценку.
Пусть серия наблюдений на уровне yi имеет вид: уi1, уi2, …, yin,, где n – число повторных наблюдений на i-м уровне. Тогда на i-м уровне среднее значение наблюдений
|
|
|
|
= |
1 |
∑ |
|
|
. |
|
|
|
|
|
(29) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а среднее значение наблюдений по всем уровням |
|
|
||||||||||||||||||
|
|
= |
1 |
|
∑ |
∑ |
|
|
= |
1 |
∑ |
̅ |
|
(30) |
||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
=1 |
|
=1 |
|
|
|
|
|
=1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Общая выборочная дисперсия всех наблюдений |
|
|
||||||||||||||||||
2 = |
|
1 |
[∑ |
|
∑ |
|
2 |
− |
1 |
(∑ |
|
∑ |
)2]. |
(31) |
||||||
|
|
|
|
|
||||||||||||||||
в |
|
−1 |
=1 |
=1 |
|
|
|
=1 |
=1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При этом разброс значений у определяется суммарным |
||||||||||||||||||||
влиянием |
случайных |
|
|
причин |
|
|
|
|
и |
|
фактора |
х. |
||||||||
Задача дисперсионного анализа состоит в том, чтобы разложить общую дисперсию D[у] на составляющие, связанные со случайными и неслучайными причинами [11].
44
Оценка генеральной дисперсии, связанной со случайными факторами,
̃ |
[ ] = |
1 |
|
|
[∑ |
|
∑ |
|
|
2 |
|
1 |
∑ |
|
(∑ |
|
|
2 |
|
|
|
|
|
=1 |
=1 |
|
|
− |
|
|
=1 |
) ] , (32) |
|||||||
0 |
|
( −1) |
|
|
|
|
|
|
|
=1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а оценка факторной дисперсии |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
̃ |
̃ |
|
|
|
̃ |
[ ]. |
|
|
|
(33) |
||
|
|
|
|
|
|
|
= [ ] − |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Учитывая, |
что факторная дисперсия наиболее заметна |
||||||||||||||||||
при анализе средних значений на i-м уровне фактора, а остаточная дисперсия (дисперсия случайности) для средних значений в n раз меньше, чем для отдельных измерений, найдем точную оценку выборочной дисперсии:
̃ |
+ |
1 |
̃ |
[ ] = |
1 |
|
∑ |
|
|
2 |
. |
(34) |
|
|
|
|
|
||||||||
|
|
|
−1 |
=1 |
( − ̅) |
|||||||
|
0 |
|
|
|
|
|
|
|||||
Умножив обе части этого выражения на n, получим в правой части выборочную дисперсию Sв2, имеющую (k–1)-ю степень свободы. Влияние фактора х будет значимым, если при заданном γ выполняется неравенство Sв2/D0[y]>F1-γ. В противном случае влиянием фактора х на результаты моделирования можно пренебречь и считать нулевую гипотезу Н0 о равенстве средних значений на различных уровнях справедливой.
Таким образом, дисперсионный анализ позволяет вместо проверки нулевой гипотезы о равенстве средних значений выборок проводить при обработке результатов моделирования проверку нулевой гипотезы о тождественности выборочной и генеральной дисперсии.
Задания:
1. При уровне значимости α = 0,05 методом дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объекта на основании пяти измерений для трех уровней фактора Ф1 − Ф3. Расчетные данные представлены в табл. 9.
45
|
|
|
Таблица 9 |
|
Расчетные данные |
|
|
Номер |
Ф1 |
Ф2 |
Ф3 |
измерения |
|
|
|
1 |
18 |
24 |
36 |
2 |
28 |
36 |
12 |
3 |
12 |
28 |
22 |
4 |
14 |
40 |
45 |
5 |
32 |
16 |
40 |
2. Рассмотрим выборочное обследование производительности труда рабочих одинаковых профессий на четырех однотипных заводах разных городов. Производительность выражена в относительных величинах по отношению к базовой, принятой за единицу. Требуется установить, существенно различаются производительности труда рабочих рассматриваемых профессий на четырех заводах. Исходные данные приведены в таблице. Принять уровень значимости, равным 0,05. Расчетные данные приведены в табл. 10.
Таблица 10
Расчетные данные
Порядковый |
|
|
Заводы |
|
|
номер |
1 |
2 |
|
3 |
4 |
1 |
1,55 |
1,62 |
|
1,69 |
1,76 |
2 |
0,70 |
0,52 |
|
0,34 |
0,17 |
3 |
0,22 |
0,12 |
|
0,47 |
0,81 |
4 |
0,38 |
0,91 |
|
1,45 |
1,99 |
5 |
1,70 |
2,79 |
|
3,89 |
|
6 |
2,88 |
4,35 |
|
5,83 |
|
7 |
10,73 |
|
|
|
|
46
Контрольные вопросы:
1.Для какой цели используется дисперсионный
анализ?
2.В чем состоит задача дисперсионного анализа?
3.Что такое факторная дисперсия?
4.Что такое критерий Фишера?
5.В связи с чем затруднено использование критериев Смирнова и Стьюдента для проверки нулевой гипотезы?
6.В каком случае влияние фактора x является
значимым?
7.В чем состоит преимущество дисперсионного
анализа?
47
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Дынкин, Е. Б. Марковские процессы [Текст]: учебник / Е. Б. Дынкин. – М.: Физматлит, 1963. – 860 с.
2.Кемени, Дж. Конечные цепи [Текст]: учебник / Дж. Кемени, Дж. Снелл. – М.: Наука, 1970. – 273 с.
3.Клейнрок, Л. Теория массового обслуживания [Текст]: учебник / Л. Клейнрок. – М.: Машиностроение, 1979. – 432 с.
4.Бочаров, П. П. Теория массового обслуживания [Текст]: учебник / П. П. Бочаров, А. В. Печинкин. – М.: РУДН,
1995. – 530 с.
5.Вентцель, Е. С. Введение в исследование операций [Текст]: учебник / Е. С. Вентцель. – М.: Советское радио, 1964. – 623 с.
6.Нейман, Дж. Теория игр и экономическое поведение [Текст]: учебник / Дж. Нейман, О. Моргенштерн – М.: Наука, 1970. – 708 с.
7.Самаров, К. Л. Элементы теории игр [Текст]: метод. пособие / К. Л. Самаров. – М.: Резольвента, 2009. – 21 с.
8.Питерсон, Дж. Теория сетей Петри и моделирование систем [Текст]: учебник / Дж. Питерсон. – М.:
Мир, 1984. – 264 с.
9.Дрейпер, Н. Прикладной регрессионный анализ [Текст]: учебник / Н. Дрейпер, Г. Смит. – М.: Статистика, 1973.
–398 с.
10.Фёрстер, Э. Методы корреляционного и регрессионного анализа [Текст]: учебник / Э. Фёрстер, Б. Рёнц.
–М.: Финансы и статистика, 1981. – 302 с.
11.Кельтон, В. Д. Имитационное моделирование процессы [Текст]: учебник / В. Д. Кельтон, А. М. Лоу. – М.: Питер. – 846 с.
48
