Методическое пособие 447

обслуживания для всех требований). Например, E3/G/2 означает, что входящий поток системы – эрланговский третьего порядка, поток обслуживания имеет произвольное распределение времени обслуживания, число обслуживающих приборов равно двум.

При формулировании задачи важную роль играет дисциплина очереди, здесь рассматривается следующая: требование приходит в систему и дожидается обслуживания, а например, не уходит, если очередь велика, и, кроме того, каждое требование обслуживается в свою очередь без какихлибо приоритетов.

Отношение λ/μ = ρ – загрузка системы (коэффициент загрузки).

Расчетные формулы для системы М/М/1 имеют следующий вид:

вероятность того, что обслуживающий прибор свободен,

Пример 1. Заявки поступают на обслуживающее устройство случайно, причем средний промежуток времени между поступлениями заявок равен 1,0 мин, среднее время обслуживания – 0,8 мин. Определить: среднее число заявок в системе; среднее время ожидания обслуживания; среднюю длину очереди, ожидающей обслуживания; среднее время; проведенное заявкой в системе; вероятность отсутствия заявок в системе, если она состоит из одного прибора и имеет пуассоновский входящий поток и экспоненциальное время обслуживания (М/М/1).

9

Решение. Так как средний промежуток времени между поступлениями заявок известен: mt пост = 1 мин, то среднее число ожидающих клиентов в течение 1 мин,

λ = 1/mt пост; λ = 1/1 = 1 клиент/мин.

Поскольку среднее время обслуживания mt обсл = 0,8 мин, то среднее число клиентов, обслуживаемых в 1 мин,

μ = 1/mtобсл ; μ = 1/0,8 = 1,25,

т. е. в среднем обслуживается более одной заявки в минуту. Тогда вероятность простоя системы

Р0 = 1 – ρ; Р0 = 1 – 0,8 = 0,2,

т. е. 20 % рабочего времени система простаивает. Среднее число клиентов в системе

E(n) = ρ/(1 – ρ); E(n) = 0,8/(1 – 0,8) = 4 клиента Среднее время ожидания в очереди

E(t) = ρ/μ(1 – ρ); E(t) = 0,8/(1,25·0,2) =3,2 мин.

Средняя длина очереди, ожидающей обслуживания,

E(n0) = ρ2/(1 – ρ); E(n) = 0,82/ (1 – 0,8) = 3,2 клиента т. е., как правило, не более трех клиентов стоят в очереди.

Среднее время, проведенное клиентом в системе, ожидая сначала в очереди, а потом и собственно своего обслуживания,

E(tc) = 1/μ(1 – ρ); E(tc) = 1/[1,25·(1 – 0,8)] = 4 мин.

Задания:

1.Построить граф состояний следующего случайного процесса: устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное случайное время.

2.Рабочий обслуживает m станков. Поток требований на обслуживание пуассоновский с параметром λ станков в час. Время обслуживания одного станка подчинено экспоненциальному закону. Среднее время обслуживания одного станка равна μ минут. Определить: 1) среднее число

10

станков, ожидающих обслуживания, 2) коэффициент простоя станка, 3) коэффициент простоя рабочего. n=1, m=3, λ=2, μ=8.

3. Пункт по ремонту радиотехники работает в режиме отказа с одним мастером. Интенсивность потока заявок 1, производительность мастера 1.3. Определить предельные значения относительной пропускной способности Q, абсолютной пропускной способности А и вероятность отказа Ротк телефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят.

Контрольные вопросы:

1.Что такое поток событий?

2.В каком случае поток называется потоком без последствий?

3.Какой поток называют стационарным?

4.Какой поток событий называют ординарным?

5.Какой поток называю пуассоновским?

6.Что является элементами СМО?

7.Какой формулой задается экспоненциальный закон?

11

Практическое занятие № 3 Моделирование с использованием метода динамики средних

Цель занятия: Рассмотреть основные понятия и математический аппарат моделирования с использованием метода динамики средних, получить практические навыки по решению задач.

Теоретические сведения

В многоэлементных системах часто целью моделирования является определение средних количеств элементов, находящихся в одинаковых состояниях.

Например, в задаче о пеленгации передатчиков противника командира интересует число запеленгированных передатчиков, а не вероятности пеленгации одного передатчика, двух, трех и т. д. Но чтобы определить среднее число их, надо знать вероятности всех возможных состояний pi, так как

Но число состояний и, следовательно, число уравнений Колмогорова может оказаться настолько большим, что вызовет непреодолимые трудности при моделировании по схеме марковских процессов.

В исследовании операций есть метод, позволяющий успешно решать такие и аналогичные задачи. Этот метод называется метод динамики средних [5].

Метод динамики средних позволяет непосредственно определять математическое ожидание числа элементов сложной системы, находящихся в одинаковых состояниях.

Метод дает приближенные результаты. Но обладает замечательным свойством: чем больше система имеет

12

элементов и состояний, тем точнее результат математического моделирования.

Для получения расчетных формул метода предположим, что имеем дело с системой, обладающей следующими признаками:

в системе протекает случайный марковский процесс;

элементы системы однородны в том смысле, что состояния, их число и их вероятности - одинаковые;

элементы меняют состояния независимо друг от друга. Схематично такая система может быть представлена

так, как показано на рис. 3.

Рис. 3. Схематичное представление системы

Система имеет N элементов, а каждый элемент имеет n состояний. Численность i -го состояния на любой момент времени - величина случайная. Обозначим ее xi(t). Матожидание и дисперсия этой случайной величины будут равны:

13

В силу однородности элементов и независимости состояний случайная величина xi имеет биномиальное распределение (распределение Бернулли) с матожиданием и

состояния элемента в произвольный момент времени с матожиданием численности этих состояний по всем элементам.

Поскольку процессы в элементах - марковские, то справедливы все рассуждения об установившихся значениях mi, об условиях существования установившихся значений mi(t) = mi.

Полученные уравнения для mi называют уже не уравнениями Колмогорова, а уравнениями динамики средних

[5]. Поскольку они получаются из уравнений Колмогорова путем умножения всех членов на постоянное число N, то их можно писать сразу для средних численностей состояний mi по образцу уравнений для вероятностей pi.

Пример 1. В части имеются 100 средств связи (СС). СС выходят из строя с интенсивностью λ12. При нахождении СС в неисправном состоянии проводится его диагностика, в результате чего оно может быть отправлено в ремонтное подразделение части (интенсивность отправки λ23), либо во внешнее ремонтное подразделение (интенсивность отправки λ24), либо списано (интенсивность списания λc). В ремонтном подразделении части СС ремонтируются с интенсивностью λ31, а во внешнем ремонтном подразделении - с интенсивностью λ41. СС части пополняются с интенсивностью λп, в среднем равной интенсивности списания.

Требуется провести моделирование с целью определения средних численностей каждого состояния СС.

Решение. Система может иметь следующие четыре состояния:

14

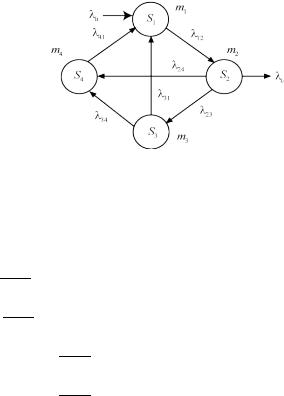
S1 - СС исправно;

S2 - СС неисправно, производится диагностика;

S3- СС находится на ремонте в ремонтном подразделении части;

S4 - СС находится на ремонте во внешнем ремонтном подразделении.

Построим размеченный граф состояний, представленный на рис. 4.

Рис. 4. Размеченный граф состояний системы ремонта

Каждое уравнение системы составляется по тому же правилу, что и система дифференциальных уравнений

Колмогорова.

1 = −12 1 + 31 3 + 41 4 + 11 2;2 = −23 2 − 24 2 − 2 + 12 1;3 = − 31 3 + 23 2;

{4 = − 41 4 + 24 2;

Численности состояний являются функциями времени, т. е. mi(t) = mi. Выражение для пополняющего члена написано из условия равенства в среднем пополнения и убылип = 2 2. Также мы не можем воспользоваться

15

нормировочным условием ∑4=1 ( ) = 100, так как в силу случайного характера списания и пополнения в некоторые моменты времени оно может не выполняться. Общее число СС в части при этом меняется со временем:

интегрирования, например, методом Рунге-Кутты, задав начальные значения численностей состояний для момента t=0:

1(0) = 100, 2(0) = 0, 3 = 0, 4 = 0,

считая интенсивности , , п известными. Дисперсия вычисляется по формуле:

= [1 − (∑4 )] , = ̅̅̅̅1,4;

=1

По дисперсии определяется среднеквадратическое отклонение численности состояний и находится диапазон возможных значений численности состояния.

Метод динамики средних справедлив и для предельных значений численностей состояний. В данной задаче уравнения динамики средних - система линейных алгебраических уравнений:

0= − 12 1 + 31 3 + 41 4 + 11 2;

{0 = − 23 2 − 24 2 − 2 + 12 1; 0 = − 31 3 + 23 2;

0 = − 41 4 + 24 2;

Однако прежде чем переходить к этим уравнениям, нужно сначала убедиться, что стационарные значения существуют. Здесь численности состояний не являются функциями времени. Поэтому можно воспользоваться нормировочным условием.

16

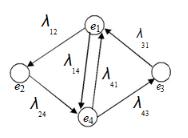
Задания:

1. Пусть дана стохастическая система, граф которой изображен на рис. 5. Вычислить предельные вероятности состояний p1, p2, p3, p4, если интенсивности потоков событий равны 12 = 2, 14 = 1, 24 = 1, 31 = 3, 41 = 2, 43 = 2.

Рис. 5. Граф системы

2. На заводе имеются 80 средств обслуживания (СО). СО выходят из строя с интенсивностью λ12. При нахождении СО в неисправном состоянии проводится его диагностика, в результате чего оно может быть отправлено в ремонтное подразделение части (интенсивность отправки λ23), либо во внешнее ремонтное подразделение (интенсивность отправки λ24), либо списано (интенсивность списания λc). В ремонтном подразделении части СО ремонтируются с интенсивностью λ31, а во внешнем ремонтном подразделении - с интенсивностью λ41. СС части пополняются с интенсивностью λп, в среднем равной интенсивности списания. Требуется провести моделирование с целью определения средних численностей каждого состояния СО.

17

Контрольные вопросы:

1.Опишите суть метода динамики средних.

2.Какие уравнения называются уравнениями динамики средних?

3.Каким свойством обладает метод динамики

средних?

4.Какие результаты дает этот метод?

5.По каким формулам вычисляются дисперсия и мат.ожидание случайной величины?

6.Какое равенство связывает вероятность i-го состояния элемента в произвольный момент времени с мат. ожиданием?

7.По каким формулам вычисляются дисперсия и мат. ожидание, считая, что случайная величина имеет биноминальное распределение?

18