Контрольные вопросы

1. В каком случае многочлен Q_n(x) делится на x-b без остатка?

2. Сколько корней имеет многочлен степени n?

3. Может ли алгебраическое уравнение не иметь ни одного решения?

3. Интегрирование простейших дробно-рациональных функций

Интегрирование любой правильной рациональной дроби (n<m) выполняется разложением этой дроби на сумму правильных простейших дробей четырех типов с последующим их интегрированием.

Простейшей дробью четвертого типа называют дробь вида

где k=2,3,…; A,B,p,q – действительные числа, причем следовательно стоящий в знаменателе квадратный трехчлен не имеет действительных корней. Такую дробь с помощью тождественных преобразований представляют в виде линейной комбинации двух дробей вида

и

Интеграл от первой дроби легко сводится к табличному

(10)

а интеграл от второй дроби после выделения полного квадрата в знаменателе и замены переменной принимает вид

где t=x+a. При k=1 этот интеграл легко вычисляется:

(11)

Если k>1, то можно с помощью интегрирования по частям выразить через :

= =

= (12)

Формулы такого типа, когда неизвестная величина, имеющая индекс k, выражается через аналогичные величины с меньшими номерами, называются рекуррентными формулами.

Формула (12) позволяет последовательно уменьшать индекс неизвестной пока в правой части не появится интеграл , который уже вычислен ранее (11).

Пример 1. Вычислить интеграл

Решение. Применяя дважды формулу (3.3), получим

.

Пример 2. Вычислить интеграл

Решение. Преобразуем заданный интеграл в сумму двух интегралов:

Вычислим первый интеграл по формуле (10), а ко второму

применим рекуррентную формулу (12):

Задания для самостоятельного решения

Вычислить интегралы:

1.

2.

3.

4. dx;

5. dx.

4. Важнейшие кривые

Алгебраические кривые первого и второго порядка подробно изучались в курсе аналитической геометрии. При этом было показано, что любое алгебраическое уравнение пер­вой степени Ах + Ву + С = 0 описывает прямую на плоскости, а уравнения второй степени являются уравнениями эллипса, гиперболы или параболы, если не принимать во внимание не­которые вырожденные случаи: точка, пара прямых, мнимый эллипс. Кроме алгебраических уравнений для задания плоской кривой могут быть использованы параметрические , и уравнения в полярной системе координат . Например, уравнение окружности с центром в точке (2, 0) и радиусом равным 2 можно задать тремя способами:

Рассмотрим алгебраические кривые более высоких по­рядков, которые нередко встречаются в приложениях.

Полукубическая парабола (рис.2). Уравнение этой кривой имеет вид или в параметрической форме

,

Локон Аньези (рис. 3). Уравнение кривой имеет вид (х² + а²) у - а³ = 0, а > 0. Кривая симметрична относительно оси Оу, имеет асимптоту у = 0и максимум в точке (0, a).

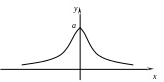
Рис.2 Рис.3

Астроида (рис.4). Уравнение этой кривой имеет вид (a > 0) или Кривая лежит в круге ; имеет две оси симметрии; при производная не существует, а при равна нулю. Параметрические уравнения кривой имеют вид

.

Кардиоида (рис.5). Уравнение этой кривой имеет вид , или в полярной системе координат , или в параметрическом виде

.

Кривая симметрична относительно оси ; пересекается с осями координат в точках , , , ; имеет максимум в точке и минимум в точке .

Рис.4 Рис.5

Рассмотрим некоторые линии механического происхождения, полученные путем качения одних кривых по другим.

Циклоида (рис.6). Циклоидой называется кривая, описываемая точкой, отстоящей на фиксированное расстояние от центра круга, катящегося без скольжения по прямой. Уравнение циклоиды в декартовой системе координат имеет вид

.

Для исследования вида этой кривой удобнее использовать параметрические уравнения

,

где - радиус катящейся окружности. Из второго уравнения системы видим, что имеет период , следовательно, также периодическая функция и ее период

Рис.6

. Поэтому исследование проведем для . Кривая пересекает ось в точках , ; ее производная положительна при , отрицательна при , а при равна нулю. Следовательно, кривая монотонно возрастает на интервале , убывает на и имеет максимум в точке , причем .

Если круг радиуса без скольжения катится извне по другому кругу радиуса , то кривую, описываемую произвольной точкой окружности подвижного круга, называют эпициклоидой (рис. 7) и ее параметрические уравнения имеют вид

,

г де - отношение радиусов катящегося и неподвижного кругов.

Рис. 7 Рис. 8

Если круг радиуса без скольжения катится внутри неподвижного круга радиуса , то кривую, описываемую произвольной точкой окружности подвижного круга, называют гипоциклоидой (рис. 8) и ее параметрические уравнения имеют вид

.

Нетрудно заметить, что эти уравнения можно получить из уравнений эпициклоиды, заменив на . На рис.8 изображены эпициклоида (а) и гипоциклоида (б) для .

Во многих случаях оказывается проще для исследования вида кривой использовать их полярные уравнения в явной или неявной формах.

В качестве примера рассмотрим трехлепестковую розу (рис. 9), заданную уравнением .

Рис. 9

Проведем исследование функции для . Поскольку то возрастает при , при принимает максимальное значение a, а при убывает от a до 0. Но имеет период Следовательно, на промежутках и кривая имеет тот же вид. Заметим, что для уточнения графика можно найти значения полярного радиуса в некоторых промежуточных точках.