
- •Кратные интегралы. Векторный анализ
- •Введение
- •1.2. Вычисление двойного интеграла в декартовых прямоугольниках. Изменение порядка интегрирования
- •1.3. Вычисление двойного интеграла в полярных координатах
- •1.4. Применение двойных интегралов для вычисления площадей и объемов
- •2. Тройные интегралы
- •2.1. Тройной интеграл. Геометрический и физический смысл тройного интеграла
- •2.2. Замена переменных в кратных интегралах
- •2.3. Тройной интеграл в цилиндрических и сферических координатах
- •2.4. Применение кратных интегралов в задачах механики и физики
- •3. Криволинейные интегралы
- •3.1. Криволинейный интеграл первого рода
- •3.2. Криволинейный интеграл первого рода, его физический смысл и механические приложения
- •3.3. Условия независимости криволинейного интеграла от пути интегрирования
- •3.4. Формула Грина. Вычисление площадей с помощью криволинейного интеграла второго рода
- •4. Поверхностные интегралы
- •4.1. Поверхностные интегралы первого рода
- •4.2. Поверхностные интегралы второго рода
- •4.3. Формула Остроградского
- •4.4. Формула Стокса
- •5. Теория поля
- •5.1. Скалярные поля
- •5.2. Векторные поля
- •5.3. Поток векторного поля. Дивергенция
- •5.4. Циркуляция векторного поля
- •5.5. Ротор векторного поля
- •6. Оператор Гамильтона
- •Заключение
- •Оглавление
- •5.5. Ротор векторного поля………….………………………156
- •6. ОПератор Гамильтона………….……………………160
- •3 94026 Воронеж, Московский просп.,14
3.2. Криволинейный интеграл первого рода, его физический смысл и механические приложения
Пусть
на плоскости хоу
задана кривая АВ,
в каждой
точке которой определена непрерывная
функция f(х,
у) двух
независимых переменных х
и у.
Рассмотрим
криволинейный интеграл I
рода (по длине дуги) от этой функции по
кривой АВ.
Он обозначается
![]() ,
кривая АВ
называется кривой интегрирования, А
– начальной,
а В – конечной
точками интегрирования. Из определения
криволинейного интеграла первого рода
следует, что он не зависит от направления
кривой АВ,
т.е.:
,
кривая АВ
называется кривой интегрирования, А
– начальной,
а В – конечной
точками интегрирования. Из определения
криволинейного интеграла первого рода
следует, что он не зависит от направления
кривой АВ,
т.е.:
![]() .
.
Если АВ – пространственная кривая, то криволинейным интегралом первого рода, распространенным на эту кривую называется интеграл вида:
![]() ,
,
где функция f(х, у, z) – функция трех независимых переменных, которая определена и непрерывна в каждой точке кривой АВ.
Масса m материальной кривой, имеющей плотность (х, у, z) равна криволинейному интегралу первого рода от функции (х, у, z) по пространственной кривой АВ, т.е.:
![]() .
(3.16)
.
(3.16)
В этом состоит физический (механический) смысл криволинейного интеграла первого рода.
Если масса распределена непрерывно вдоль дуги плоской кривой АВ с плотностью функции = (х, у) в каждой точке кривой, то статические моменты Мх и Му дуги относительно координатных осей ОХ и ОУ соответственно определяются по формулам:
![]() ;
;
![]() .
(3.17)
.
(3.17)
Моменты инерции этой дуги относительно координатных осей ОХ и ОУ соответственно равны:
![]() ;
;
![]() .
(3.18).
.
(3.18).
Координаты центра тяжести дуги АВ вычисляются по формулам:
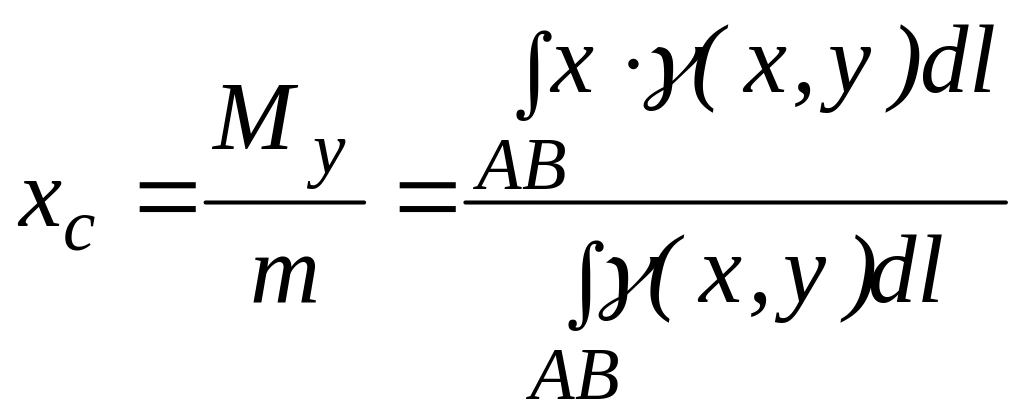 ;
(3.19)
;
(3.19)
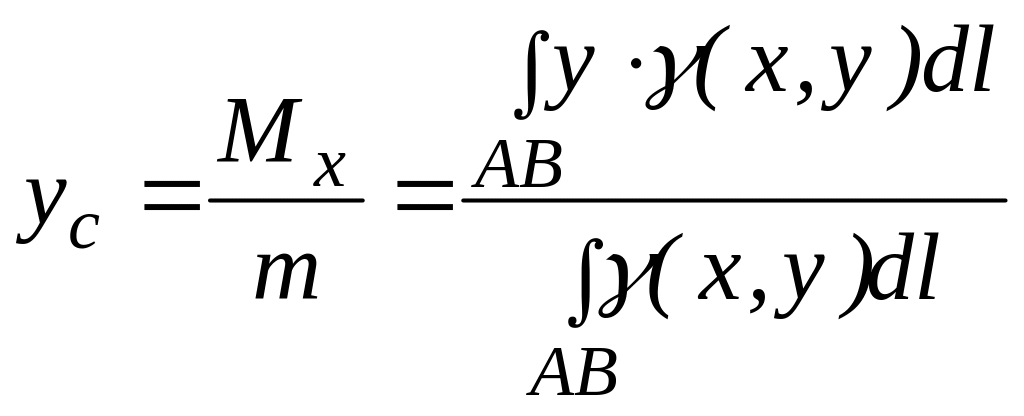 .
(3.20)
.
(3.20)
Если кривая однородна, то плотность функции (х, у) = const, поэтому формулы (3.19) и (3.20) примут вид:
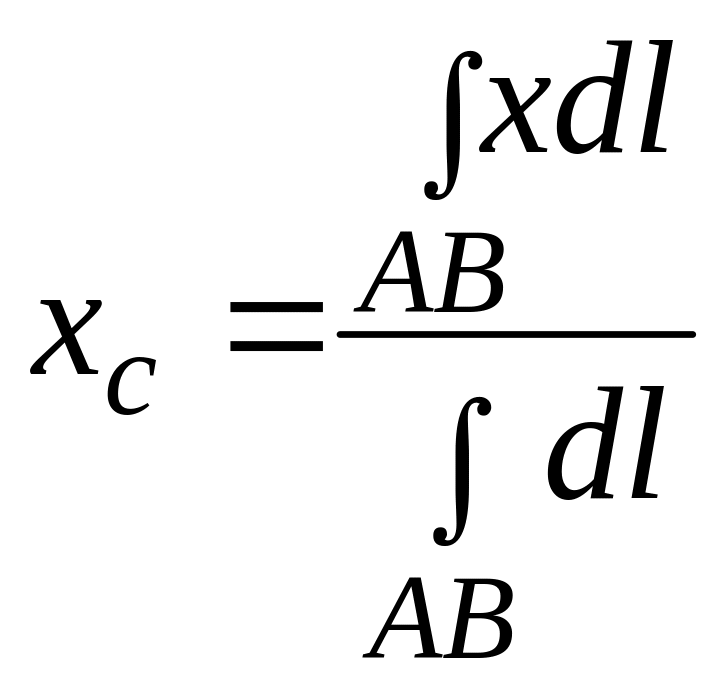
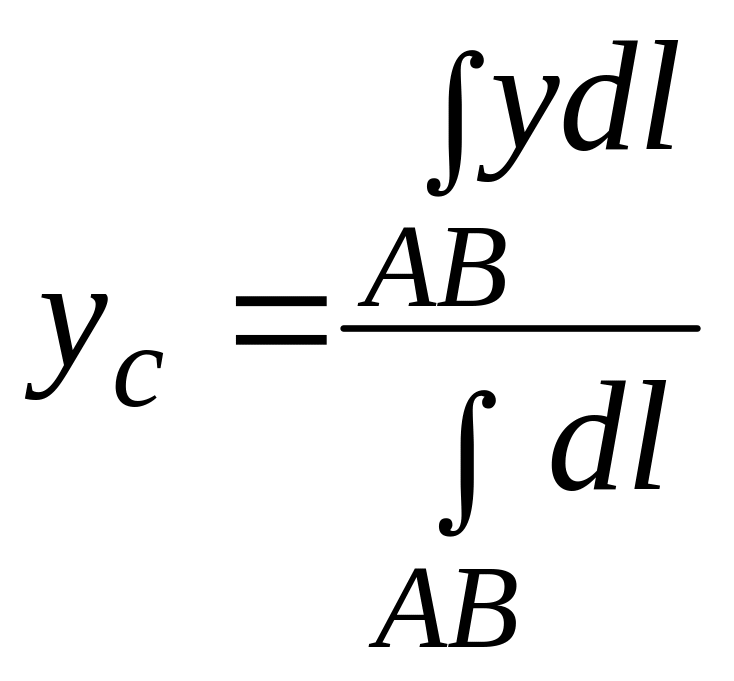 ,
(3.21)
,
(3.21)
где
![]() - длина дуги АВ.
- длина дуги АВ.
Если плоская гладкая кривая АВ задана параметрическими уравнениями вида х = х(t); у = у(t), причем, существуют непрерывные производные хt и уt, где параметр t применяется на дуги АВ в пределах t .
Тогда
![]() и криволинейный интеграл выражается
через определенный по формуле:
и криволинейный интеграл выражается
через определенный по формуле:
![]() .
(3.22)
.
(3.22)
Если кривая АВ задана уравнением у = у(х); где а х b, то
![]() .
(3.23);
.
(3.23);
Рассмотрим теперь случай пространственной гладкой кривой АВ. Пусть ее параметрические уравнения имеют вид:
х = х(t); у = у(t); z = z(t); причем существуют непрерывные производные хt, уt и zt. Предположим, что параметр t изменяется в пределах t .
Тогда справедлива формула:
![]()
![]() .
(3.24)
.
(3.24)
Криволинейный интеграл от функции f(х, у) по дуге, заданной уравнением в полярных координатах r = r(), где , вычисляется с помощью формулы:
![]() .
(3.25)
.
(3.25)
Задача
3.3.
Вычислить
![]() ,
где АВ
часть окружности х2
+ у2
= R2,
лежащая в
I
четверти.
,
где АВ
часть окружности х2
+ у2
= R2,
лежащая в
I
четверти.
Решение.
Выразим из
уравнения окружности явно ординату у
через абсциссу х,
получим
![]() (в первой четверти у
0).
(в первой четверти у
0).
Найдем
![]() и подставим в выражения
и подставим в выражения
![]() ;
;
![]() .
.
По формуле (3.23) получим:
![]() .
.
Ответ:
![]() .
.
Задача 3.4.
Найти центр тяжести полуокружности х2 + у2 = R2, лежащей в верхней полуплоскости, а также ее момент инерции относительно оси ОХ (плотность считать равной единице).
Решение.
Центр тяжести
дуги кривой определяется по формуле
(3.20). Из соображений симметрии следует,
что он находится на оси ОУ.
Поэтому хс
= 0.
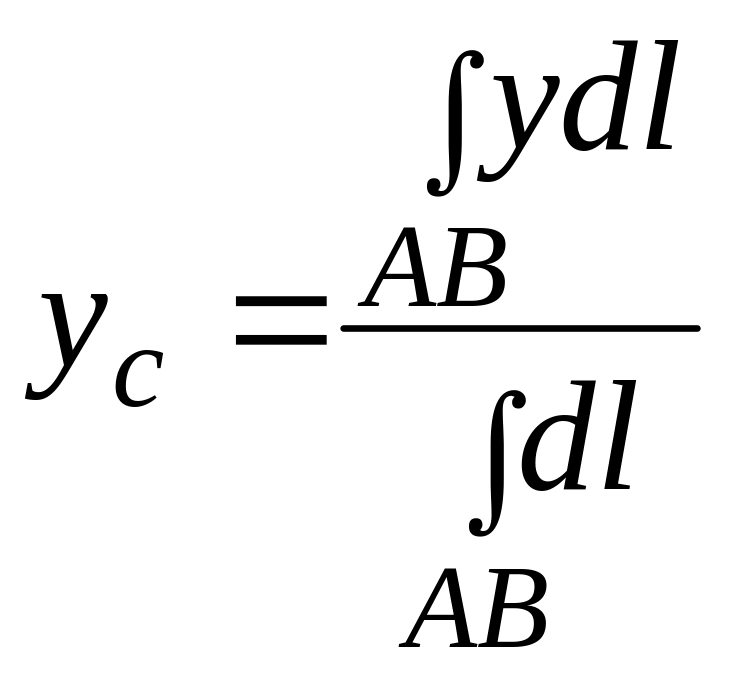 ,
где
,
где
![]() ,
так как это длина полуокружности.
,
так как это длина полуокружности.
Для вычисления числителя дроби воспользуемся параметрическими уравнениями окружности: x = R cos t; y = R sin t.
Тогда
![]() .
.
![]() ;
;
![]() .
.
Ответ:
хс
= 0,
![]() .
.
Задачи для самостоятельного решения
Задача 3.5. Найти координаты центра тяжести одной арки циклоиды: x = a(t – sin t), y = a(1 – cos t), 0 t 2.
(Считать плотность равной единице).
Указание. Воспользоваться формулами (3.22).
Учитывая симметрию, заключаем, что абсцисса центра тяжести хс = а.
![]() ;
;
![]()
![]()
![]() .
.
Ответ:
хс
= а;
![]() .
.
Задача
3.6.
Найти массу
участка кривой у
= ln
x
от точки с абсциссой
![]() до точки с абсциссой
до точки с абсциссой
![]() ,
если плотность в каждой точке равна
квадрату ее абсциссы.
,
если плотность в каждой точке равна
квадрату ее абсциссы.
Указание.
![]() ;
;
![]() .
.
Ответ:
![]() .
.
Задача 3.7.
Определить
центр тяжести дуги астроиды x
= a
cos3t,
y
= a
sin3t,
лежащий в
первой четверти
![]() .
Плотность считать равной единице.
.
Плотность считать равной единице.
Ответ:
![]() .
.
Определение криволинейного интеграла
второго рода и его механический смысл
Рассмотрим задачу, приводящую к понятию криволинейного интеграла второго рода. Эта задача о вычислении работы переменной силы при перемещении материальной точки вдоль некоторой кривой.
Предположим,
что при движении по кривой АВ
материальная точка М переходит из
положения А в положение В. Во
время движения на точку М действует
сила
![]() =
=
![]() (x,
y, z),
заданная своими проекциями P,
Q, R
на координатные оси OX,
OY и OZ,
т.е.
(x,
y, z),
заданная своими проекциями P,
Q, R
на координатные оси OX,
OY и OZ,
т.е.
= P(x, y, z)![]() + Q(x, y, z)
+ Q(x, y, z)![]() + R(x, y, z)
+ R(x, y, z)![]() .
(3.26)
.
(3.26)
Найдем работу Е силы при данном перемещении точки.
Если бы перемещение
точки М было прямолинейным, а
действующая сила
– постоянной (по величине и направлению),
то работа Е этой силы, по известной
формуле из физике, была бы равна скалярному
произведению вектора на вектор перемещения
![]() ,
т.е. Е =(
,
).
Однако особенность задачи состоит в
том, что перемещение точки является
криволинейным, а действующая сила
переменной . Разобьем кривую АВ на
части (элементарных дуг) точками М0,
М1, М2,…, Мn-1,
Mn
где M0
совпадает с А, а Mn
– с точкой В. Обозначим диаметр
разбиения через d.
На каждой дуге выберем производную
точку
,
т.е. Е =(
,
).
Однако особенность задачи состоит в
том, что перемещение точки является
криволинейным, а действующая сила
переменной . Разобьем кривую АВ на
части (элементарных дуг) точками М0,
М1, М2,…, Мn-1,
Mn
где M0
совпадает с А, а Mn
– с точкой В. Обозначим диаметр
разбиения через d.
На каждой дуге выберем производную
точку
![]() (
,
,
(
,
,
![]() )
и найдем в ней значение силы
)
и найдем в ней значение силы
![]() =
(Pк, Qк,
Rк),
где Pк = P
(
,
,
),
Qк = Q(
,
,
),
Rк =
R(
,
,
).
Предположим, что сила сохраняется
постоянной в точках дуги и под ее действие
точка перемещается на каждом элементарном
участке не по дуге, а по хорде, соединяющей
точки Мк-1, Mк(к
= 1, 2, …, n).
Используя формулу для вычисления
скалярного произведения через проекции
силы и векторы перемещения, получим
приближенное значение работы на каждом
элементарном участке дуги
=
(Pк, Qк,
Rк),
где Pк = P
(
,
,
),
Qк = Q(
,
,
),
Rк =
R(
,
,
).
Предположим, что сила сохраняется
постоянной в точках дуги и под ее действие
точка перемещается на каждом элементарном
участке не по дуге, а по хорде, соединяющей
точки Мк-1, Mк(к
= 1, 2, …, n).
Используя формулу для вычисления
скалярного произведения через проекции
силы и векторы перемещения, получим
приближенное значение работы на каждом
элементарном участке дуги
Ек P ( , , )xк + Q( , , )yк + R( , , )zк,
xк = xк - xк-1, yк = yк - yк-1, zк = zк - zк-1, а xк , yк , zк, координаты точки Mк
(к = 1, 2, …, n).
Суммируя полученные частичные работы, найдем приближенно полную работу силы при перемещении точки М вдоль кривой АВ
E
![]()
![]() P
(
,
,
)xк
+ Q(
,
,
)yк
+
P
(
,
,
)xк
+ Q(
,
,
)yк
+
+ R( , , )zк]. (3.27)
За работу E силы при перемещении материальной точки вдоль кривой АВ примем предел суммы (3.27) при стремлении диаметра разбиения к нулю, т.е.
E
=
![]() P
(
,
,
)xк
+ Q(
,
,
)yк
+ R(
,
,
)zк].
P
(
,
,
)xк
+ Q(
,
,
)yк
+ R(
,
,
)zк].
Перейдем к определению криволинейного интеграла второго рода.
Пусть в пространстве
OXYZ задана
непрерывная, гладкая кривая АВ и
функция P(x,
y, z)
на этой кривой. С помощью точек М0,
М1, М2,…, Mn
в направлении от А и В разобьем
на n дуг производные
длины. На каждой дуге М0,
Мк-1, Mк
выберем производную точку
(![]() ,
,
)
и найдем в ней значение функции P(
,
,
)
. Для каждой элементарной дуги
вычислим произведение P(
,
,
)xк,
где xк
– проекция дуги Мк-1, Mк
на ось ОХ, т.е. xк
= xк -
xк-1,
где xк и xк-1
соответственно абсциссы конца и
начала хорды Мк-1, Mк.
Просуммируя полученные произведения,
получим
,
,
)
и найдем в ней значение функции P(
,
,
)
. Для каждой элементарной дуги
вычислим произведение P(
,
,
)xк,
где xк
– проекция дуги Мк-1, Mк
на ось ОХ, т.е. xк
= xк -
xк-1,
где xк и xк-1
соответственно абсциссы конца и
начала хорды Мк-1, Mк.
Просуммируя полученные произведения,
получим
P ( , , )xк. (3.28)
Суммы вида (3.28) называются интегральными суммами второго рода для функции P(x, y, z), соответствующими разбиению {Mк} кривой АВ (относительно координаты х) с отмеченными точками ( , , ).
определение. Предел интегральных сумм вида (3.28) при d 0 (n ), если он существует и не зависит от способа разбиения кривой АВ на частные дуги и выбора точек , называется криволинейным интегралом второго рода по координате х и обозначается
![]() (x,
y, z)dx , т.е.
(x,
y, z)dx , т.е.
(x, y, z)dx = P ( , , )xк . (3.29)
Аналогично определяются криволинейные интегралы по координатам y и z, их обозначают
![]() (x,
y, z)dy и
(x,
y, z)dy и
![]() (x,
y, z)dz , беря
для функции
(x,
y, z)dz , беря
для функции
Q(x, y, z) проекции yк на ось ОY, а для R(x, y, z) проекции zк на ось ОZ.
Определение. Сумма трех интегралов (x, y, z)dx,
(x, y, z)dy, (x, y, z)dz называется общим криволинейным интегралом второго рода (по координатам) и обозначается
(x, y, z)dx = (x, y, z)dy + (x, y, z)dz. (3.30)
Если P, Q, R – проекции силы на координатной оси, то из формулы (3.27) следует, что общий криволинейный интеграл второго рода выражает работу этой силы на пути АВ, т.е.
E = (x, y, z)dx + (x, y, z)dy + (x, y, z)dz (3.31)
В этом состоит физический смысл криволинейного интеграла второго рода.
Замечание 1. Если кривая АВ лежит в плоскости ХОY и функции P(x,y) и Q(x,y) не зависят от z, то криволинейные интегралы второго рода имеют вид
(x, y)dx + Q(x, y)dy. (3.32)
Замечание 2. В отличие от криволинейного интеграла первого рода криволинейный интеграл второго рода меняет свое значение на противоположное при изменении направления кривой АВ, т.е.
(x,
y, z)dx = -![]() (x,
y, z)dx
(x,
y, z)dx
В самом деле, если изменить направление обхода кривой, то изменятся знаки проекций xк в сумме (3.28), значит и сама сумма, и ее предел.
Замечание 3. Криволинейный интеграл второго рода обладает всеми свойствами криволинейного интеграла первого рода, за исключением одного: он меняет знак на противоположный при изменении направления обхода кривой.
Замечание
4. В случае,
когда кривая АВ
– замкнутая (т.е. точка В
совпадает с точкой А)
употребляется обозначение
![]() (M)dx
+ Q(M)dy
+ R(M)dz.
(M)dx
+ Q(M)dy
+ R(M)dz.
В случае, когда кривая АВ замкнутая, за положительное направление обхода принимается такое, при котором область, лежащая внутри этого контура остается слева по отношению к точке, совершающей обход.
Теорема: Если функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны, или имеют конечное число разрывов первого рода вдоль непрерывной кривой АВ, имеющей конечную длину, то криволинейные интегралы
(x, y, z)dx, (x, y, z)dy, (x, y, z)dz, а
следовательно и криволинейный интеграл
dx + Qdy + Rdz существуют.
Вычисление криволинейного интеграла второго рода
Пусть гладкая кривая АВ задана параметрическими уравнениями х= х(t), y=y(t), z=z(t), причем изменению t от до соответствует движение точки по кривой от А до В (не обязательно, чтобы было меньше ). Тогда
![]() =
=
![]() . (3.33)
. (3.33)
Аналогичные формулы имеют место и для интегралов по координатам y и z. Выпишем формулу для вычисления общего интеграла второго рода
![]() +Q(x,y,z)dy+R(x,y,z)dz=
+Q(x,y,z)dy+R(x,y,z)dz=
=![]() +Q(x(t),y(t),z(t))y(t)+
+Q(x(t),y(t),z(t))y(t)+
+R(x(t),y(t), z(t))z(t) ] dt. (3.34)
Если АВ – кривая, расположенная, например, в плоскости ХОУ, то формула (3.34) в этом случае примет вид
![]() =
=![]() +
+
+Q(x(t),y(t),z(t))y(t) + R(x(t),y(t),z(t))z(t)dt. (3.35)
Для плоской гладкой кривой у = у(х), где а х b, заданной явным уравнением, получим
![]() =
=
=![]() .
(3.36)
.
(3.36)
Задача
3.8. Вычислить
криволинейный интеграл
![]() ,
где АВ
– одни виток винтовой линии
,
где АВ
– одни виток винтовой линии
х= cos t, у = sin t, z = 2t от точки А (1,0,0) до точки В (1,0,4).
Решение. Вдоль дуги АВ параметр t изменяется от 0 до 2. Тогда, используя формулу (3.24), получим
=
![]() =
=
=![]() =
=![]() .
.
Задача
3.9. Вычислить
криволинейный интеграл
![]() вдоль
кривой у=х3
от точки А
(1,1) до
точки В(2,8).Решение.
По формуле (3.26) получим
вдоль
кривой у=х3
от точки А
(1,1) до
точки В(2,8).Решение.
По формуле (3.26) получим
=
![]() .
.
Связь между криволинейными интегралами
первого и второго рода.
Пусть АВ – направленная пространственная кривая с началом А и концом В, тогда все касательные к АВ также являются направленными прямыми. Обозначим углы, которые образует касательная к АВ с осями ОХ, ОУ, ОZ соответственно , и . Очевидно, что эти углы являются функциями координат x,y,z точки касания М.
Выделим из АВ элементарную дугу dl, и будем считать ее прямолинейной. Значит dl –это вектор с проекциями dx, dy, dz, направленный так же, как и кривая АВ. Следовательно, dx = cos dl, dy = cos dl, dz = cos dl.
Тогда общий интеграл второго рода выразится через интеграл первого рода по формуле
![]() =
=
![]() .
(3.37)
.
(3.37)
По формуле (3.37) осуществляется переход от криволинейного интеграла первого рода к интегралу второго рода.
Формула Остроградского - Грина.
Рассмотрим на плоскости ХОУ компактную фигуру Ф, ограниченную замкнутой гладкой (или кусочно – гладкой) кривой A.
Пусть
функции Р(х,у)
и Q(х,у)
непрерывны вместе со своими частными
производными
![]() на компактной фигуре Ф.Тогда
имеет место формула
на компактной фигуре Ф.Тогда
имеет место формула
![]() =
=![]() ,
(3.38)
,
(3.38)
которая называется формулой Остроградского-Грина. Она устанавливает связь между двойным интегралом по некоторой плоской области и криволинейным по контуру, ограничивающему эту область, играет фундаментальную роль в векторном анализе.
Докажем справедливость формулы (3.38). Рассмотрим в плоскости ХОУ выпуклую в направлении обеих осей фигуру Ф, ограниченную замкнутым контуром А, состоящим из двух кривых
у = у1(х) и у = у2(х), где у1(х) у2(х),
Рис.
3.2
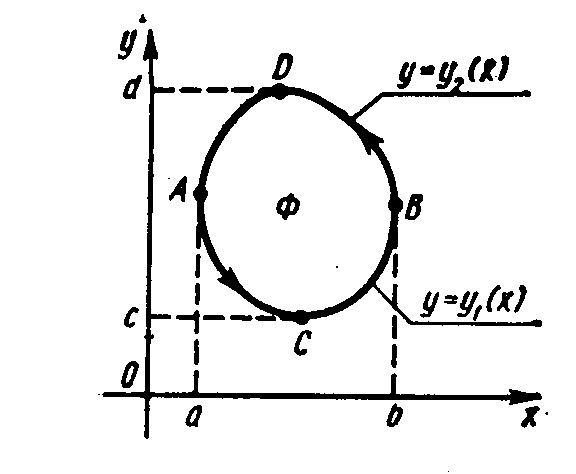
а
х
b
(рис. 3.2). Так как по условию Р(х,у)
и Q(х,у)
непрерывно дифференцируемые функции
на Ф,
то существует
![]()
![]() ,
который можно преобразовать следующим
образом
,
который можно преобразовать следующим
образом
![]() =
=
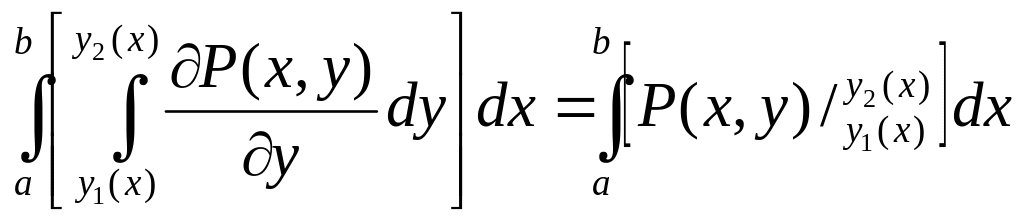 =
=
=![]() .
.
(3.39)
Если взять в качестве параметра х и записать параметрическое уравнения кривой АDВ в виде х = х, у = у2(х), а кривой АСВ – в виде х = х, у = у1(х), то используя ранее выведенные формулы, получим
![]() ;
;![]() .
.
(3.40)
Подставляя выражение (3.40) в (3.30) и учитывая свойства криволинейных интегралов, имеем
![]()
. (3.41)
Аналогично можно доказать, что
![]() .
(3.42)
.
(3.42)
Вычитая (3.41) из (3.42), получим формулу
![]() .
.
(в предположении, что обход контура А осуществляется против часовой стрелки). Формула (3.38) доказана для выпуклой фигуры Ф.
Однако она справедлива и для всякой замкнутой области, которую можно разбить на конечное число выпуклых фигур.
Замечание. При доказательстве формулы (3.36) рассматривалась область Ф, ограниченная одним замкнутым контуром (односвязная). Можно доказать, что формула Остроградского-Гаусса остается справедливой и для многосвязной области, ограниченной не одним, а несколькими не связанными друг с другом контурами (многосвязной).
Геометрические и механические приложения
криволинейных интегралов
Криволинейные интегралы имеют широкие приложения в геометрии, механике и физике. Ограничимся рассмотрением только некоторых из них. Площадь плоской области
Используя формулу Грина (3.38), выведем формулы для вычисления площади фигуры Ф с помощью криволинейного интеграла.
Если
функции Р(х,у)
= -у, а Q(х,у)=0,
то
![]() и формуле
(3.38) примет вид
и формуле
(3.38) примет вид
![]() .
Откуда S
= -
.
Откуда S
= -![]() .
(3.43)
.
(3.43)
Аналогично, полагая Р(х, у) = 0, Q(х, у) = х, получим
S
= -![]() (3.44)
(3.44)
При Р(х, у) = -1/2 у; Q (х, у) = 1/2 х, имеем
S
= 1/2![]() .
.
Задача
3.10. Найти
площадь S
плоской фигуры, ограниченной эллипсом
![]() .
.
Решение. Параметрические уравнения эллипса имеют вид x = а соs t, y = b sin t, где 0 t 2.
По формуле (3.44) находим
S=
=
![]() .
.
Координаты центра масс материальной кривой
Для определения координат центра масс материальной кривой АВ, если известна линейная плоскость распределения массы (М) в каждой ее точке М, используются формулы
 ,
(3.45)
,
(3.45)
где
M
=
![]() -масса
кривой АВ.
-масса
кривой АВ.
Если кривая АВ однородна, то есть = const, то формулы (3.45) упрощаются
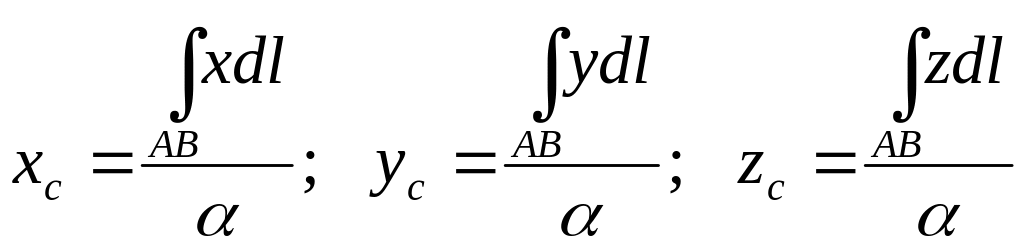 .
(3.46)
.
(3.46)
где
=
![]() -кривой
АВ.
-кривой
АВ.
Задача
3.11. Вычислить
![]() ,
где АВ –
первая четверть окружности х2
+ у2
= R2,
пробегаемая
против часовой стрелки.
,
где АВ –
первая четверть окружности х2
+ у2
= R2,
пробегаемая
против часовой стрелки.
Решение. Из уравнения окружности выразим у через х.
Получим
![]() ,
так как в первой четверти у
0, то
,
так как в первой четверти у
0, то
![]() ;
;
![]() .
.
Учитывая, что интегрирование ведется против часовой стрелки х изменяется от R до 0.
По формуле (3.29) получим:
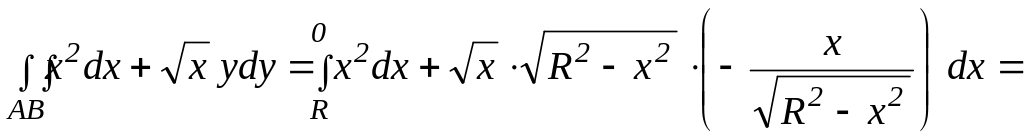
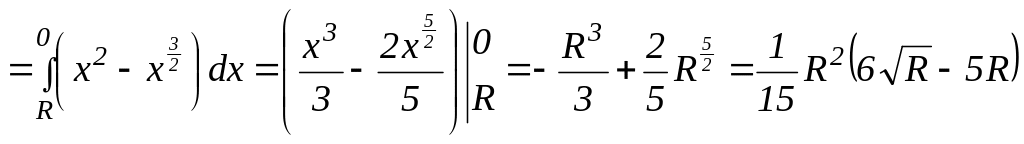
Ответ:
![]() .
.
Задача
3.12. Вычислить
криволинейный интеграл,
![]() где АВ один
виток линии х
= cos
t,
где АВ один
виток линии х
= cos
t,
y = sin t, z = 2t от точки А(1, 0, 0) до В(1, 0, 4).
Решение. Очевидно, что вдоль дуги АВ параметр t изменяется от 0 до 2. По формуле (3.28), получим
![]()
![]() .
.
Ответ:
![]() .
.
Задачи для самостоятельного решения
Задача
3.13. а) Вычислить
![]() ,
где АВ – дуга
параболы у
= х2
от точки х
= 0 до точки
х = 2;
,
где АВ – дуга
параболы у
= х2
от точки х
= 0 до точки
х = 2;
б)
Вычислить![]() ,
где АВ та
же дуга.
,
где АВ та
же дуга.
Ответ:
а)
![]() ;
б)
;
б)
![]() .
.
Задача
3.14.
Вычислить
![]() ,
где АВ
,
где АВ
1) отрезок прямой, соединяющий точки А(2, 3) и В(3, 5);
2) дуга параболы у = х2 (0 х 2);
3) дуга параболы у=х2, соединяющая точки С(0,0) и D(4,2).
Ответ:
1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Задача 3.15. Вычислить:
![]() ;
;
где L одна из линий, соединяющих точки О(0, 0) и А(2, 2).
отрезок ОА;
парабола
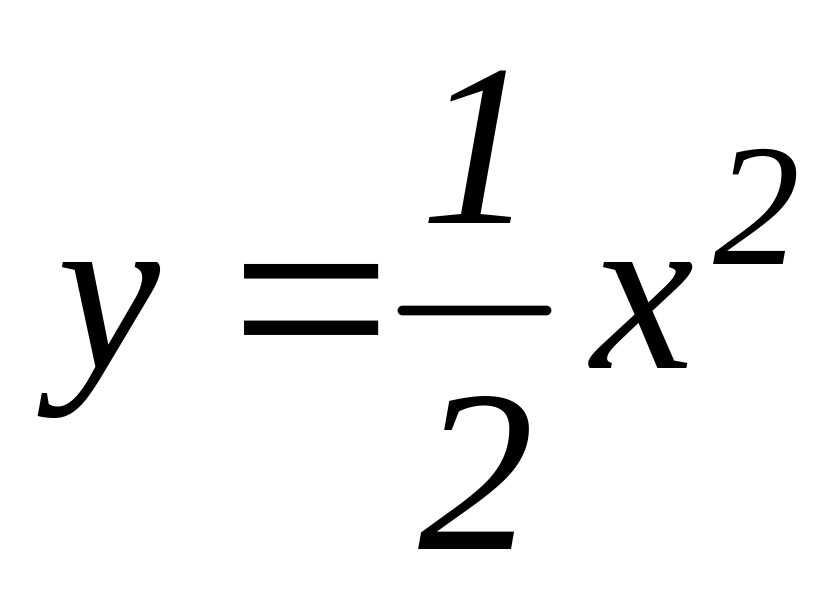 ;
;парабола
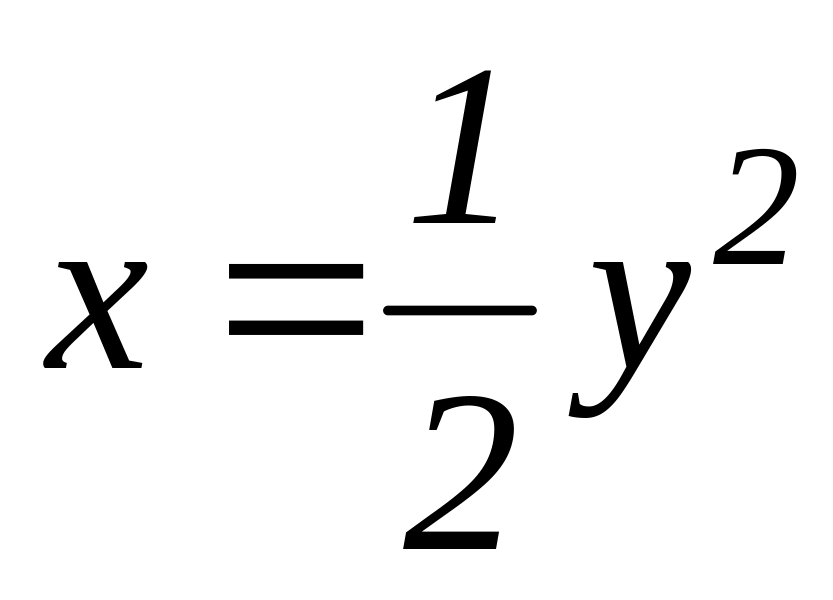 ;
;кубическая парабола
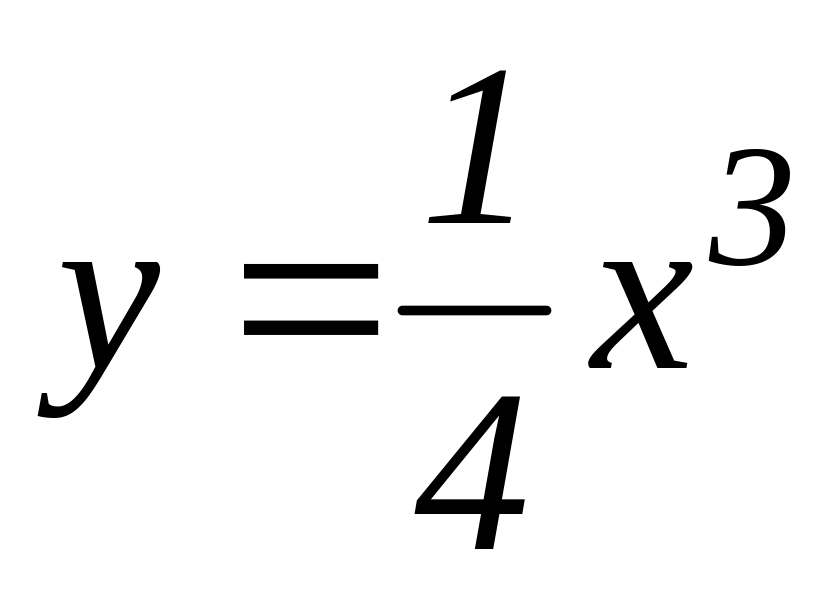
ломанная ОСА, где С(2, 0).
Решение.
Уравнение прямой на которой лежит отрезок ОА у = х, поэтому dy = dx. Заменим в подынтегральном выражении у на х, а dy на dx, получим:
![]() .
.
Из уравнения кривой следует, что dy = xdx.
Заменяя
в подынтегральном выражении у
на
![]() ,
а dy
на
хdx,
получим, что
,
а dy
на
хdx,
получим, что
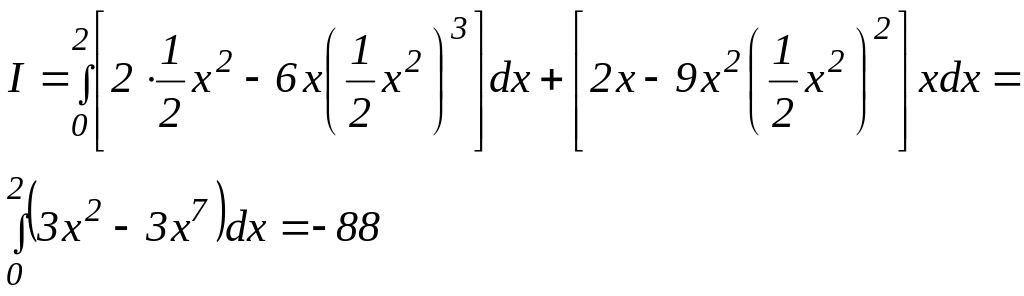
Так как уравнение линии , то dx = ydy. Заменим в подынтегральном выражении х, на
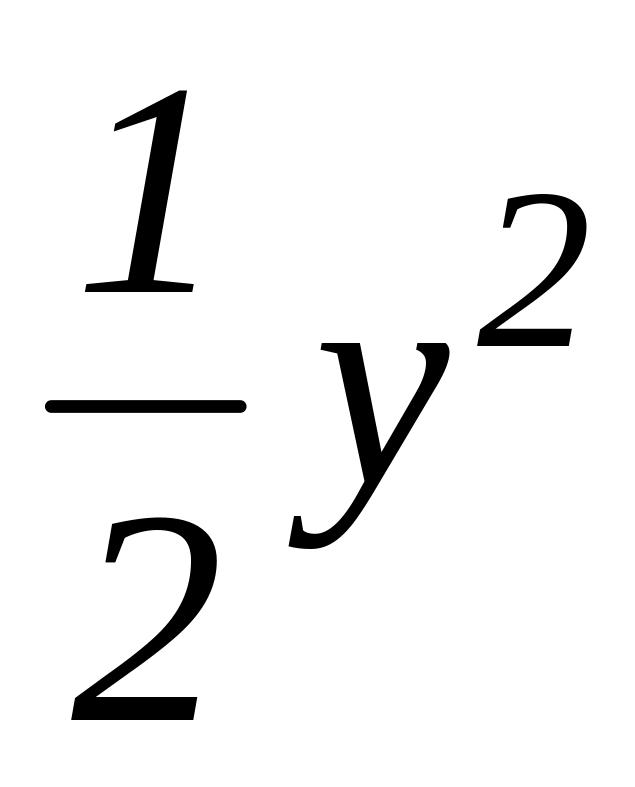 ,
а dx
на ydy,
получим, учитывая, что у
изменяется от 0
до 2.
,
а dx
на ydy,
получим, учитывая, что у
изменяется от 0
до 2.
![]()
![]() .
.
Убедиться самостоятельно, что I = - 88.
Вычислим этот интеграл по ломанной ОСА, состоящий из отрезка ОС оси ОХ и отрезка СА прямой Х = 2.
В этом случае на отрезке ОС: у = 0, dy = 0. На отрезке СА: х = 2, dх = 0, а у изменяется от 0 до 2, так как
![]() .
.
![]() .
.
Итак, по какой бы из указанных кривых, соединяющих точки (0, 0) и (2, 2), мы не вычисляли этот интеграл, оказывается, что он равен одному и тому же числу. Иначе говоря, величина этого интеграла не зависит от пути интегрирования.
Ниже будет указано условие, которому должно удовлетворять подынтегральное выражение Р(х,у)dx + Q(x,y)dy в криволинейном интеграле второго рода, чтобы интеграл не зависел от пути интегрирования, соединяющего эти точки.
