1.3. Вычисление двойного интеграла в полярных координатах

В полярных координатах dS = rdrd, x = rcos, y = rsin, где r – полярный радиус (0  r  +),  – полярный угол (0    2), а двойной интеграл:

. (1.18)

Рис. 1.11

Область D должна быть отнесена к полярной системе координат (рис. 1.11),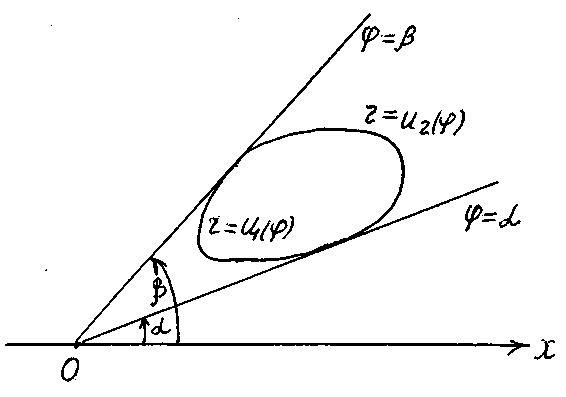

если она ограничена двумя лучами с уравнениями  =  и  = (  ) и линиями, определяемыми уравнениями r = u₁() и r = u₂(), где функции u₁() и u₂() непрерывны на отрезке [, ], однозначны и сохраняют аналитическое выражение, то двойной интеграл, распространенный на эту область, вычисляется по формуле 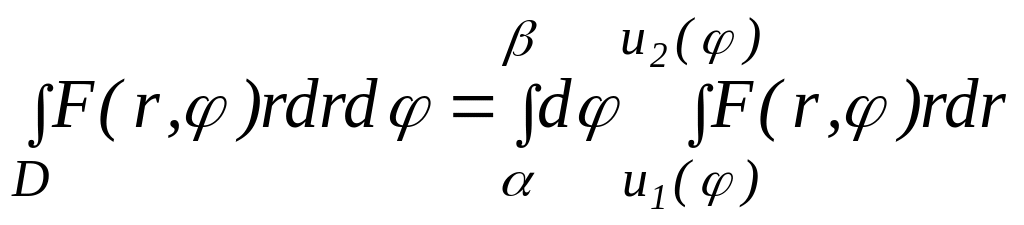(1.19):

. (1.19)

Интеграл, стоящий в правой части этой формулы – повторный (иначе двукратный). Во внутреннем интеграле  следует рассматривать как величину постоянную.

Задача 1.7. Вычислить , где область D ограничена линиями r = R и r = 2R sin.

Решение. Область D ограничена окружностями радиуса R, одна из них с центром в начале координат (r = R), а другая с центром в точке с координатами (O, R) на оси ОУ (рис. 1.12).

Рис. 1.12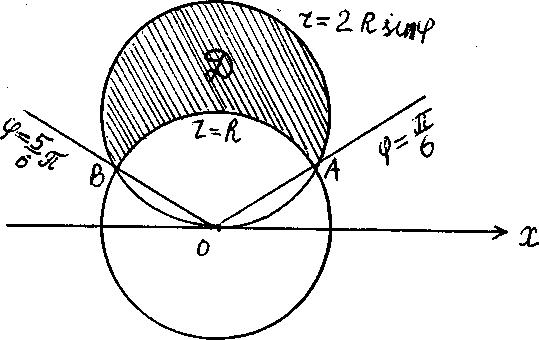

Чтобы определить, как изменяется в области D полярный угол , проведем лучи из начала координат в точки А и В. Решая систему уравнений , найдем значения угла , соответствующие лучам ОА и ОВ.

Получим 2R sin = R; sin = , , .

Таким образом, пределы изменения полярного угла  в области D от до .

Теперь найдем пределы изменения полярного радиуса в области D. Для этого под произвольным углу , взятым в промежутке , проведем из полюса О луч ОР. В точке С входа этого луча в область D r = R, а в точке Р выхода из области r = 2R sin, поэтому полярный радиус изменяется в области D R до 2R sin.

Поэтому .

(Мы вынесли sin за знак внутреннего интеграла, так как при вычислении внутреннего интеграла переменная  сохраняет постоянное значение).

Внутренний интеграл равен

Внешний интеграл равен

.

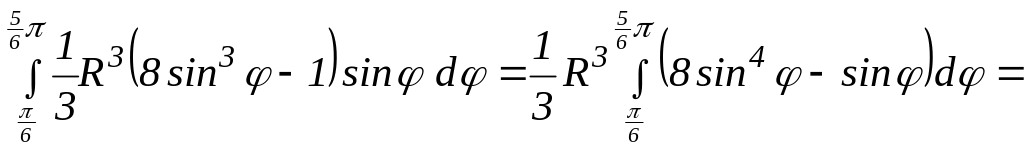
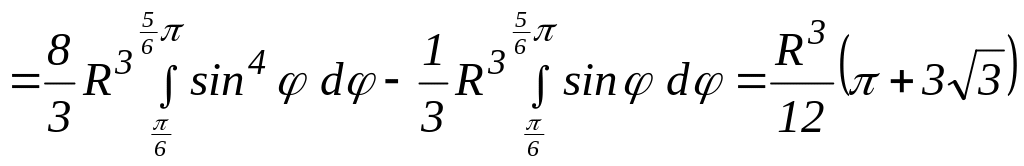Указание. При вычислении следует использовать тригонометрические формулы .

Задача 1.8. Вычислить двойной интеграл , где область D ограничена полярной осью и кривой r²=a²cos2 .

Решение. Кривая r² = a²cos2 – лемниската.

В области D полярный угол изменяется от 0 до .

Рис. 1.13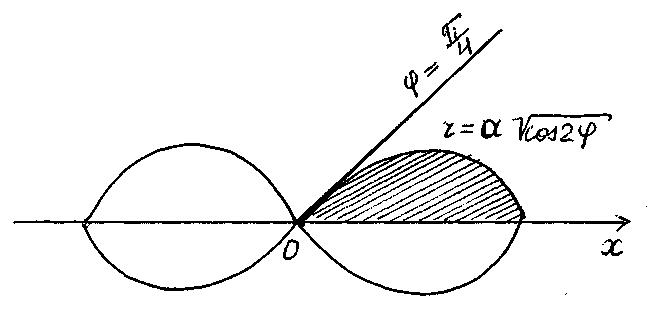

Верхний предел изменения  можно получать из уравнения лемнискаты, подставив r = 0, то есть a²cos2 = 0; cos2 = 0, , .

(Учтено условие ). Нижний предел получается из условия, что область D ограничена полярной осью. Чтобы определить пределы изменения полярного радиуса области D, проведем луч из полюса О, пересекающий область D под произвольным углом  . Он входи в область D в полюсе, то есть при r = 0, а выходит в точке на лемнискате, в котором r = a .

Получим: = .

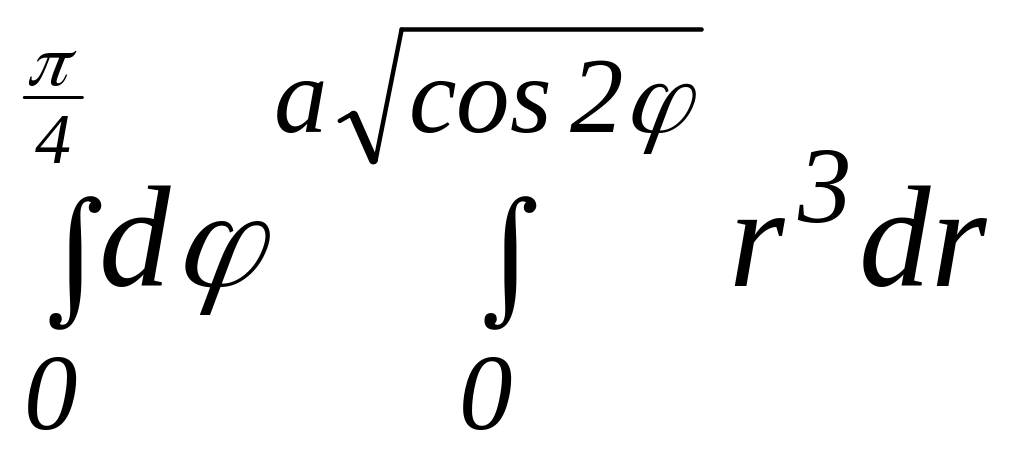Внутренний интеграл равен

.

Внешний интеграл равен

.

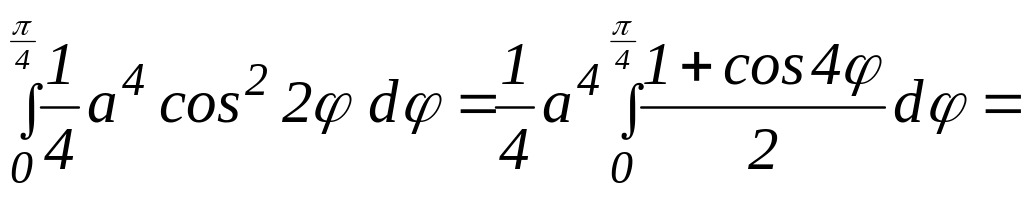
Ответ: .

Задачи для самостоятельного решения

Задача 1.9. В интеграле перейти к полярным координатам.

Ответ: .

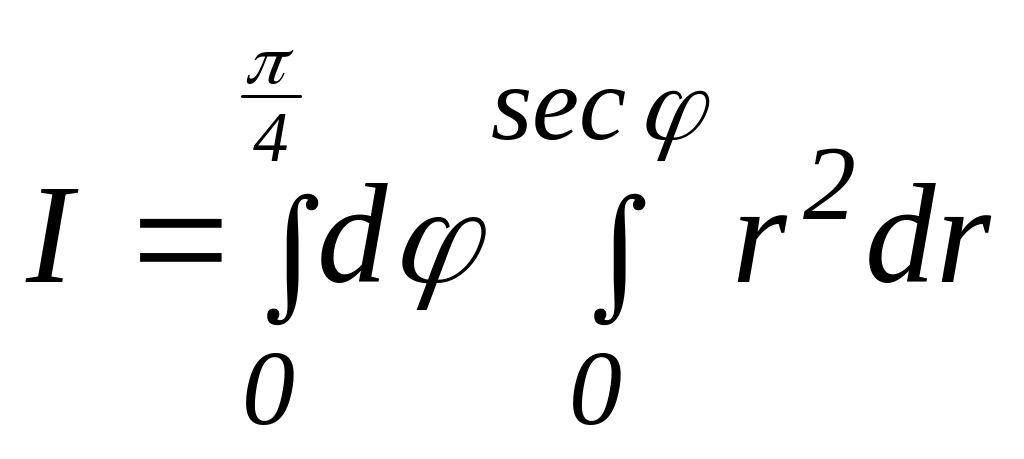1.4. Применение двойных интегралов для вычисления площадей и объемов

а) Вычисление площадей плоских фигур

Площадь плоской фигуры вычисляется по формуле:

,

где  дифференциал площади.

Если фигура отнесена к прямоугольной системе координат, то предыдущая формула примет вид:

. (1.20)

Если фигура отнесена к полярной системе координат, то ее площадь вычисляется по формуле:

. (1.21)

Задача 1.10. Найти площадь фигуры, ограниченной линиями (х – а)² + у² = а² и х² + (у – а)² = а².

Рис. 1.14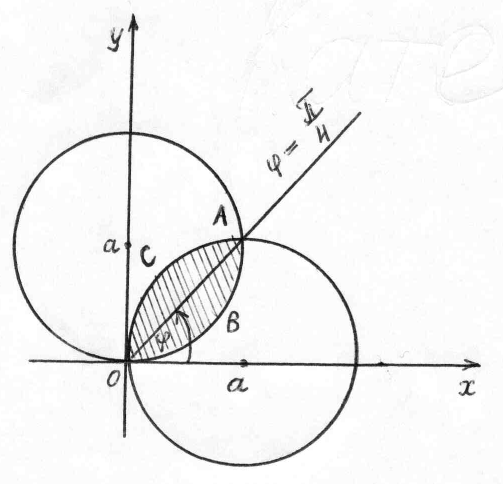

Решение.

Линии, ограничивающие область, это окружности с центрами в точках (а, 0) и (0, а) радиуса а.

Наличие в уравнении кривой выражения х² + у² указывает на целесообразность перехода к полярным координатам по формулам:

х² + у² = r².

Если раскрыть скобки, то уравнения окружностей запишутся в виде:

х² + у² – 2ах = 0;

х² + у² – 2ау = 0.

В полярных координатах они примут вид:

r = 2 acos (1.22)

r = 2 asin (1.23)

Луч ОА делит искомую площадь на две части D₁ и D₂ (рис. 1.14). Решая совместно уравнения (1.22) и (1.23) получим, что точка А лежит на биссектрисе первого координатного угла. Уравнение луча ОА: .

Искомая площадь области D = D₁  D₂ в силу свойства аддитивности двойного интеграла равна:

.

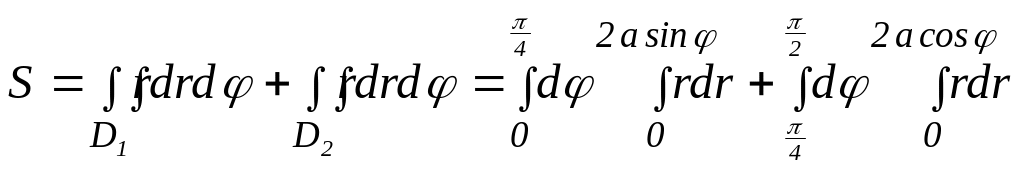Вычислим отдельно внутренние интегралы:

;

.

Поэтому искомая площадь равна:

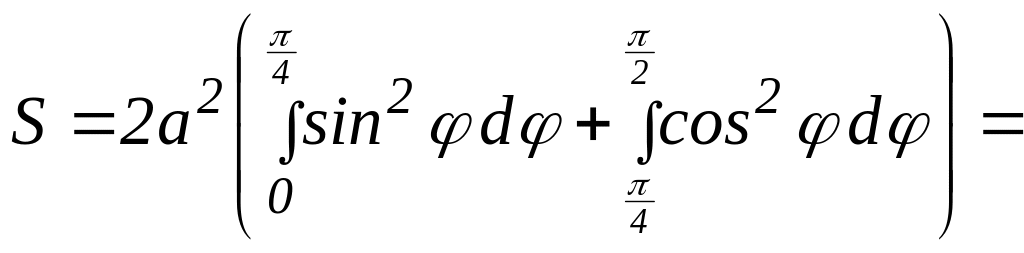
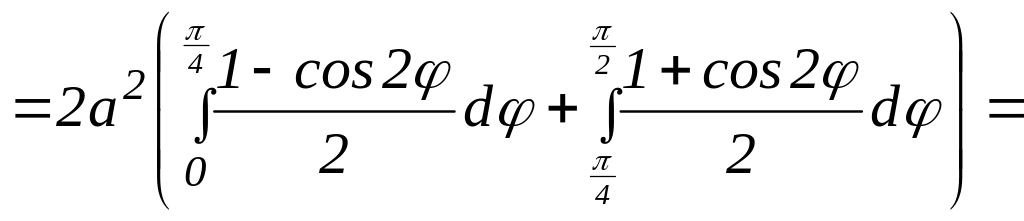
кв. ед.

Замечание. Так как из рис. (1.14) видно, что искомая площадь области D состоит из двух равных между собой по площади областей D₁ и D₂, то .

Задачи для самостоятельного решения

Задача 1.11. Найти площадь, ограниченную линиями х² + у² – 2ах = 0 и х² + у² – ах = 0.

Указание. Уравнение линий преобразовать к полярным координатам. Получим

.

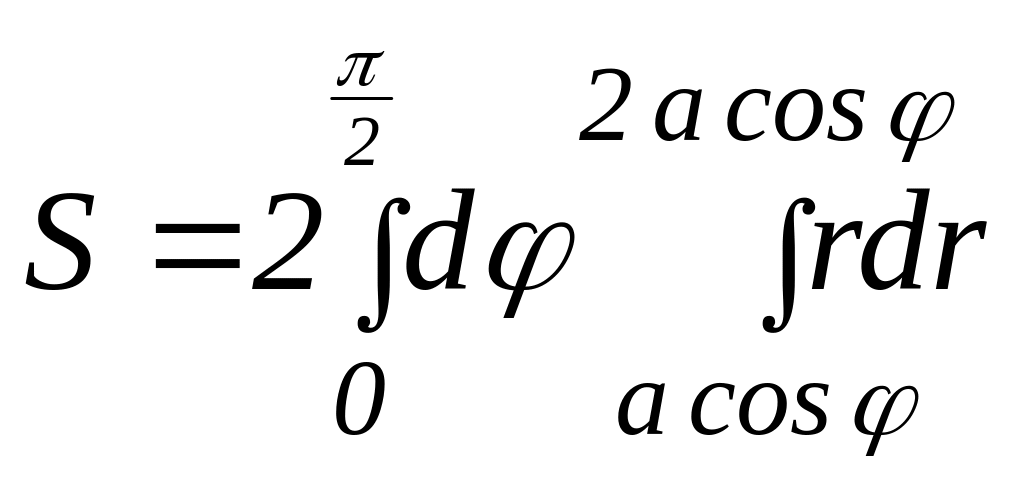Ответ: кв. ед.

Задача 1.12. Найти площадь, ограниченную линиями: х² + у² = R², х² + у² – 2Ry = 0 и х = 0.

Указание. Перейти к полярным координатам, получим

.

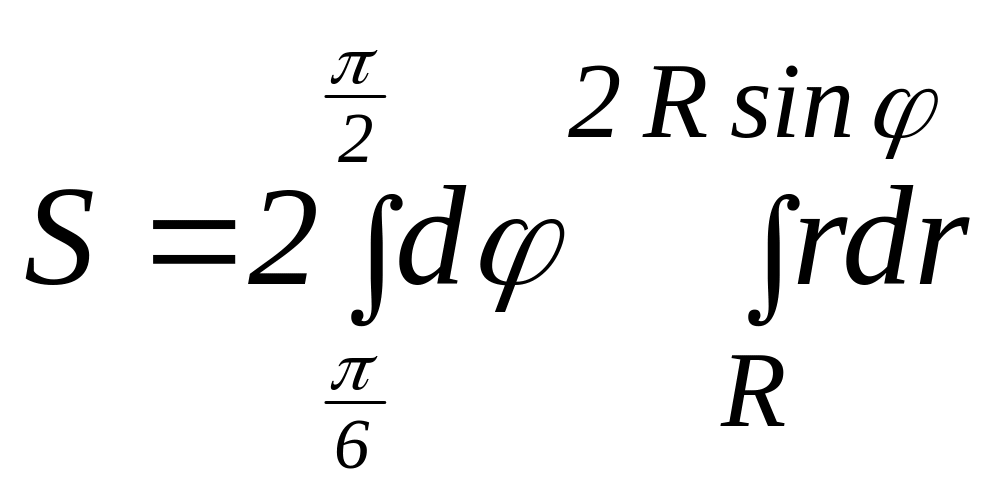Ответ: кв. ед.

б) Вычисление объемов тел

Рис. 1.15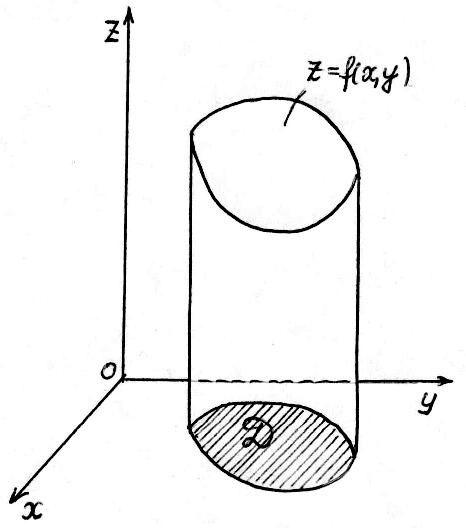

Двойной интеграл равен объему цилиндрического тела, ограниченного с боков цилиндрической поверхностью, образующие которой параллельны оси OZ. Направляющей служит контур z, ограничивающий область интегрирования D, лежащую в плоскости ХОУ и являющуюся нижним основанием этого цилиндрического тела. Сверху тело ограничено поверхностью, определяемой уравнением z = f(x, y) (рис. 1.15). Таким образом, объем такого цилиндрического тела равен

V= . (1.24)

Если вычисления ведутся в полярных координатах, то предыдущая формула примет вид:

. (1.25)

Предполагается, что функция z = f(x, y) непрерывна и однозначна в области D.

Задача 1.13. Вычислить объем тела, ограниченного поверхностями z = 4x² + 2y² + 1, x + y – 3 = 0, x = 0, y = 0, z = 0.

Решение. Первая поверхность представляет собой эллиптический параболоид с осью симметрии OZ. Он пересекает ось OZ в точке (0, 0, 1) (рис. 1.16).

Рис. 1.16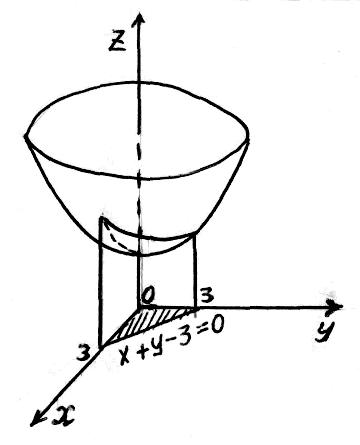

Поверхность x + y – 3 = 0 – это плоскость, параллельная оси OZ, а остальные поверхности – это координатные плоскости. На плоскость ХОУ поверхность проектируется в треугольник D, ограниченный координатными осями и прямой x + y – 3 = 0. Сверху тело ограничено поверхностью z = 4x² + 2y² + 1. Объем тела вычисляется по формуле (1.24).

куб. ед.

Ответ: V = 45 куб. ед.

Задачи для самостоятельного решения

Задача 1.14. Определить объем тела ограниченного поверхностями z = 4 – x², y = 5, y = 0, z = 0.

Указание. В формулу (1.24) подставить z из уравнения поверхности, ограничивающей сверху это тело (параболический цилиндр с образующими, параллельными оси ОУ) z=4–x².

Рис. 1.17

Учесть симметрию тела относительно плоскости УOZ (рис. 1.17). Переходя к повторному интегралу, получим .

Ответ: куб. ед.

Задача 1.15. Вычислить объем тела, ограниченного поверхностями: z = a²–x²; x+y = a, у = 2х, у = 0.

Рис. 1.18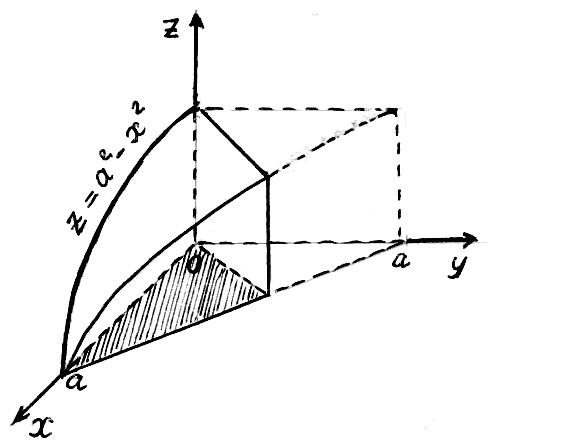

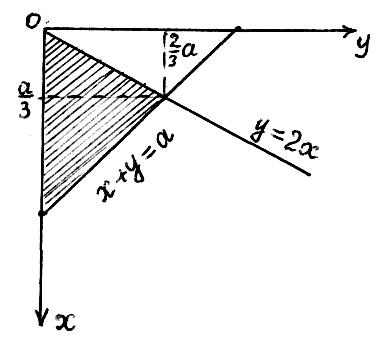
Указание. Поверхность z = a² – x² – параболический цилиндр. Эта поверхность ограничивает тело сверху. Проекция тела на плоскость ХОУ представляет собой треугольник

(рис. 1.18). По формуле (1.24) получим

Ответ: куб. ед.

Рис. 1.19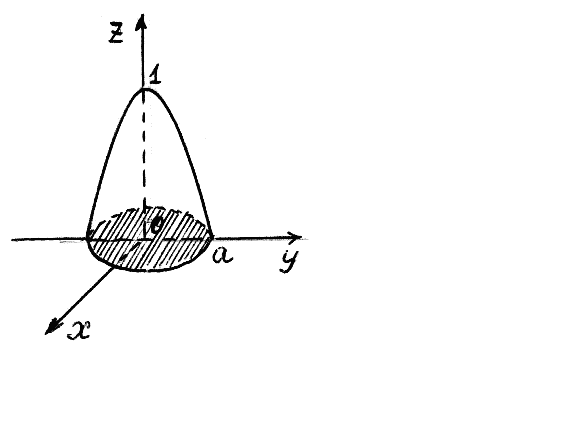

Задача 1.16. Найти объем тела, ограниченного поверхностями x²+y²+a²z=a²; z = 0.

Указание. Поверхность представляет собой параболоид вращения. Наличие слагаемого x²+y² в уравнении поверхности указывает на то, что удобно перейти к полярным координатам. Область интегрирования – это круг радиуса а

(рис. 1.19). Уравнение поверхности параболоида в полярных координатах имеет вид

r²+a²z = a²;

.

Ответ: куб. ед.

Задача 1.17. Вычислить объем тела, ограниченного поверхностями 2х + у – 2 = 0; 4х + 3у – 2z = 0 и координатными плоскостями.

Ответ: куб. ед.

в) Вычисление площади поверхности

Если поверхность задана уравнением z = f(x, y), то плоскость той части поверхности, которая проектируется на плоскость ХОУ в область D_ХОУ вычисляется по формуле

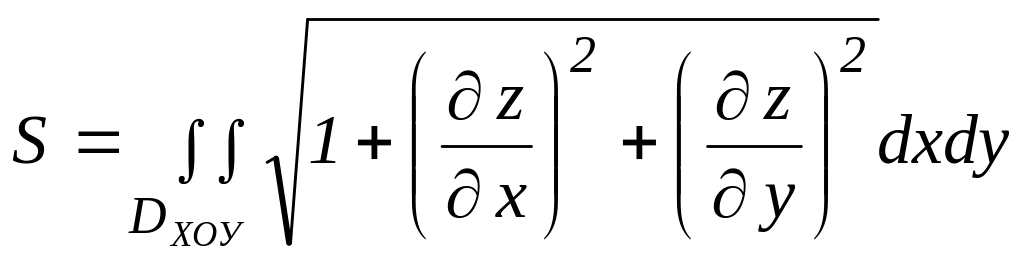. (1.26)

Предполагается, что функция z = f(x, y) непрерывна и однозначна в области D и имеет в этой области непрерывные частные производные и .

Иногда выгодно проектировать поверхность, площадь которой вычисляется, не на плоскость ХОУ, а на плоскость УOZ, тогда уравнение поверхности следует решить относительно переменной x = x(y, z).

Получим формулу:

. (1.27)

Если поверхность, площадь которой вычисляется, проектируется на плоскость XOZ, тогда уравнение поверхности следует решить относительно переменной у = у(x, z).

Получим формулу:

. (1.28)

Задача 1.18. Вычислить площадь той части поверхности

у = x² + z², которая находится в первом октанте и ограничена плоскостью у = 2.

Решение.

Поверхность, площадь которой требуется вычислить, часть параболоида вращения (ось вращения ОУ) находящаяся в первом октанте, и ограничена плоскостью у = 2, перпендикулярной к оси ОУ.

Спроектируем вычисляемую поверхность на плоскость XOZ. Тогда получим четверть круга, ограниченного окружностью (рис.1.20), уравнение которой получим, исключая у, из двух уравнений:

Рис. 1.20

Уравнение этой окружности: х²+z²=2 ; у = 0.

Так как мы проектировали поверхность на плоскость XOZ,то ее уравнение должно быть решено относительно переменной у и следует воспользоваться формулой (1.28).

Из условия задачи у = х²+z²; .

Получим формулу:

, где область интегрирования

четверть круга радиуса .

Наличие под корнем выражения х² + z² указывает на то, что целесообразно ввести полярные координаты, учитывая, сто в этих координатах х² + z² = r². Полярный угол изменяется в пределах от 0 до , а полярный радиус от 0 до . Получим:

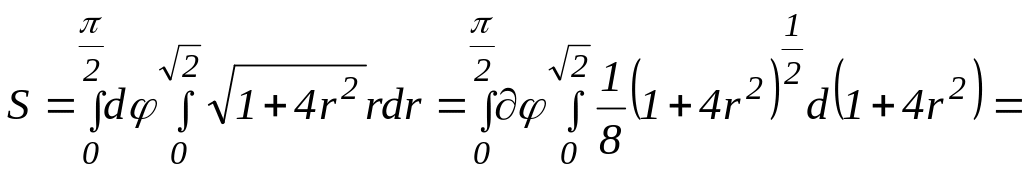
Ответ:

Задачи для самостоятельного решения

Задача 1.19. Найти площадь поверхности, вырезанную цилиндром x²+у²=1, из сферы x²+у²+z²=4.

Рис. 1.21

Указание. Спроектировать вычисляемую поверхность на плоскость XOУ (рис. 1.21). Вычислить часть искомой площади находящейся в первом октанте. Проекцией будет четверть круга, ограниченного окружностью x²+у²=1.

Уравнение сферы решить относительно переменной z. Получится . Воспользуемся формулой (1.26). После перехода к полярным координатам получим:

Ответ:

Задача 1.20. Найти площадь поверхности, ограниченной конусом z²= x² + у² и плоскостью z = 2.

Рис. 1.22

Указание. Спроектировать поверхность на плоскость XOУ. Проекцией является круг, ограниченный окружностью

x² + у² = 4 (рис. 1.22). Уравнение поверхности решить относительно переменной z получим Воспользоваться формулой (1.26). Перейти к полярным координатам.

Ответ:

Задача 1.21. Вычислить площадь поверхности шара радиуса а

Ответ: S = 4а² кв. ед.