2. Тройные интегралы

2.1. Тройной интеграл. Геометрический и физический смысл тройного интеграла

Определение тройного интеграла

Определение тройного интеграла аналогично определениям определенного и двойного интегралов.

П

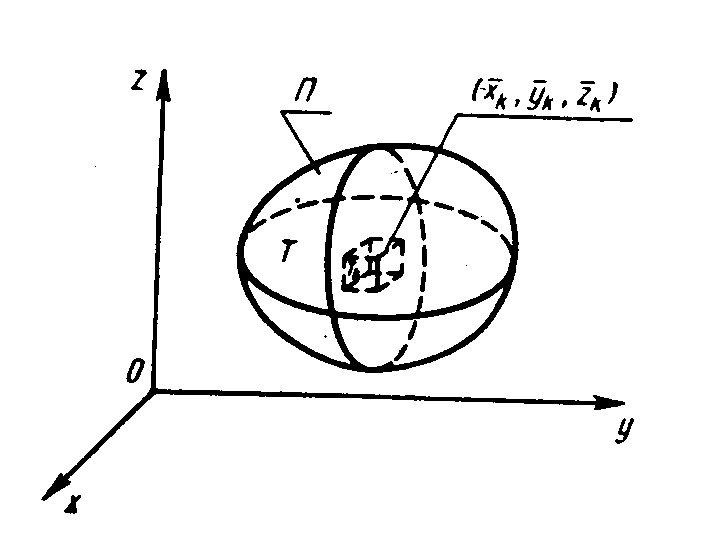Рис. 2.1

усть на пространственном компактом теле Т R³ задана функция

f: TR. Рассмотрим разбиение {T_к} тела Т с диаметрами d_k и объемами V_к (к = 1, …, n) (рис. 2.1). Наибольший из диаметров d_k назовем диаметром произведенного разбиения и обозначим через d.

В каждом частичном теле T_к выберем произвольную точку ( ) и составим сумму

J_n = V_к. (2.1)

Суммы вида (2.1) называются трехмерными интегралами. Суммами Римана функции f(x, y, z), соответствующими разбиению {T_к} с отмеченными точками ( ).

Определение 1. Предел трехмерных интегральных сумм вида (2.1) при d  0 (если он существует) называется тройным интегралом (по Риману) от функции f(x, y, z) по области Т и обозначается . Таким образом

= V_к. (2.2)

В этом случае функция f(x, y, z) называется интегрируемой (по Риману) в области Т, переменные x, y, z - переменными интегрирования; f(x, y, z) - подынтегральной функцией; dV = dxdydz - элементом объема в декартовых прямоугольных координатах, Т – областью интегрирования.

Геометрический и физический смысл

тройного интеграла

Тройной интеграл по области Т от функции f(x, y, z)  1 на Т равен объему этого тела. В декартовых прямоугольных координатах получим

= . (2.3)

В этом состоит геометрический смысл тройного интеграла. Доказательство этого утверждения непосредственно следует из определения тройного интеграла.

Тройной интеграл по области Т от плотности (x, y, z) материального тела Т равен массе этого тела

m = . (2.4)

Эта формула выражает физический смысл тройного интеграла. Доказательство этого утверждения аналогично доказательству подобного утверждения в двумерном случае.

Свойства тройных интегралов

Можно доказать, что если подынтегральная функция непрерывна на компактном теле Т с кусочно-гладкой границей, то тройной интеграл (2.2) всегда существует.

Свойства тройных интегралов аналогичны свойствам двойных интегралов. Ограничимся перечислением этих свойств. Предполагаем непрерывность подынтегральных функций в рассматриваемых областях.

1. Тройной интеграл по области Т равен объему этого тела.

2. Свойство аддитивности

Если пространственная область Т разбита на две непересекающиеся области T₁ и T₂, то

= + .

3. Свойство линейности

Если функции f₁ и f₂ интегрируемы в области Т, то и функция c₁f₁ + c₂f₂, где c₁ и c₂ – любые вещественные константы, также интегрируема в области Т, причем

=c₁ +

+c₂ .

4. Свойство монотонности

Если всюду в области Т выполняется неравенство f₁(x, y, z)  f₂(x, y, z), то

 .

5. Абсолютная величина тройного интеграла не превосходит тройного интеграла от абсолютной величины подынтегральной функции, т.е.

│ │  .

6. Теорема о среднем. Если функция f(x, y, z) непрерывна в замкнутой ограниченной области ТR³, то в этой области найдется точка ( )T, что =

=V f( ), где V – объем области Т.

7. Если функция f(x, y, z) непрерывна в замкнутой ограниченной области Т R₃, то mV ≤  MV, где m и M – наименьшее и наибольшее значение функции f(x, y, z) в области V.

Вычисление тройных интегралов в декартовых

прямоугольных координатах

Пусть область интегрирования Т – компактное тело, выпуклое вдоль оси ОZ, ограничено снизу и сверху соответственно гладкими поверхностями z=z₁(x, y) и z₂(x, y), причем проекция тела Т на плоскость ХОУ есть плоская фигура Ф_ху (рис.2.2). Поэтому при фиксированных (х, у)Ф_ху соответствующие аппликаты Z точек тела Т изменяются в пределах z₁(x, y)  z  z₂(x, y).

Рис. 2.2

Рис. 1.10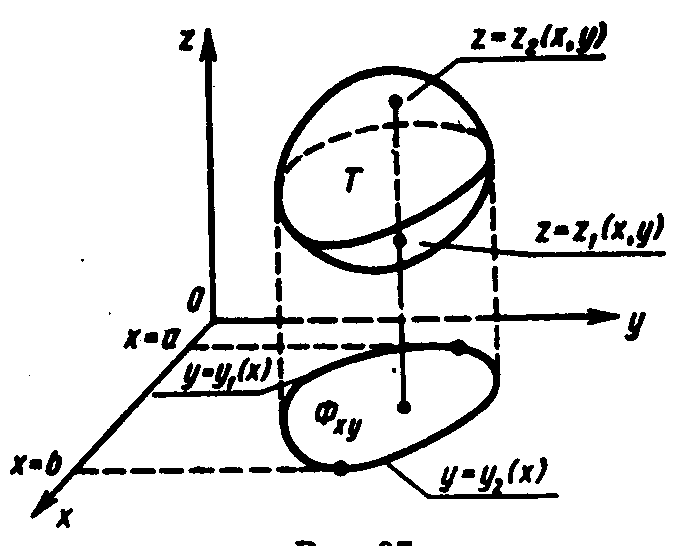

Можно получить

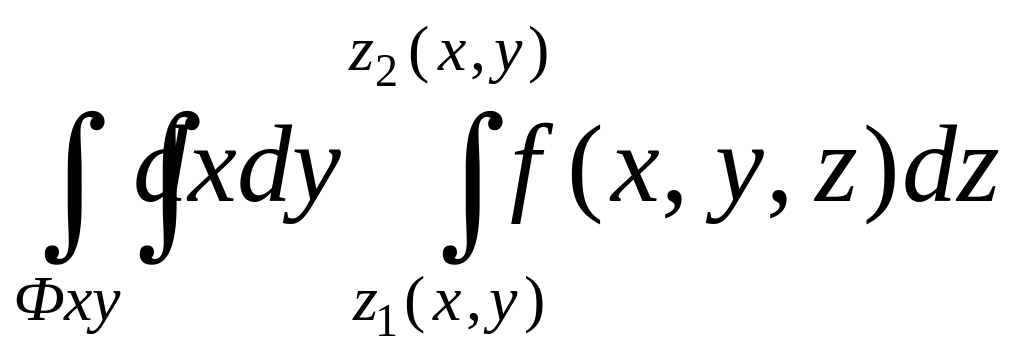= (2.5)

Предположим, что фигура Ф_ху выпукла вдоль оси ОУ, то есть определяется неравенствами а  х b, у₁(x)  у у₂(x), где у₁(x) и у₂(x) – непрерывные функции на отрезке а, b.

Тогда

= . (2.6)

Из формул (2.5) и (2.6) получим:

= (2.7)

Интеграл в правой части (2.7) называется повторным интегралом.

Если прямые, параллельные оси ОZ, пересекут тело Т более чем в двух точках, то надо разбить его на части так, чтобы для каждой из этих частей указанные прямые пересекали тело не более, чем в двух точках. Затем применить свойство аддитивности тройного интеграла. Вычисляя по формуле (2.7) для каждой из полученных частей тройной интеграл и складывая полученные результаты, найдем интеграл по всему телу Т.

Если Т – прямоугольный параллелепипед, образованный плоскостями х = а₁, х = b₁; у = а₂, у = b₂; z = а₃, z = b₃, то все пределы постоянны и результат интегрирования не зависит от порядка, в котором производится интегрирование

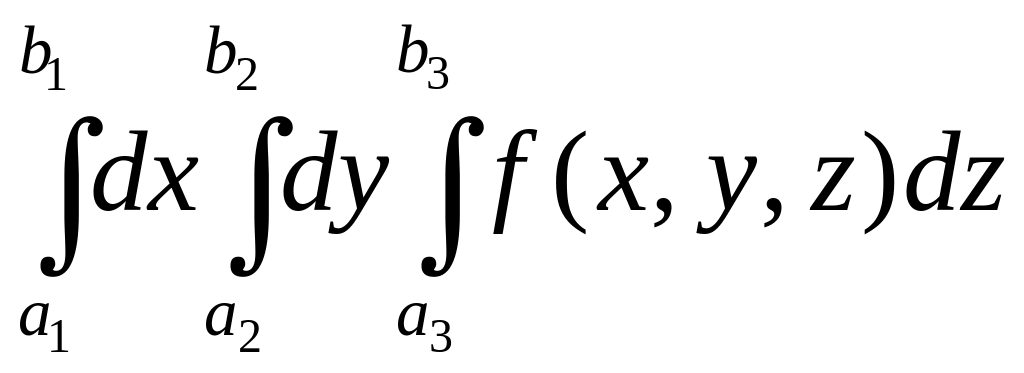= . (2.8)

Таким образом, для вычисления тройного интеграла, необходимо:

1. Проверить условие выпуклости области.

Если область выпукла вдоль оси ОZ, то составить выражение вида (2.7), в котором z = z₁(x, y) и z = z₂(x, y) – уравнения линий, представляющих собой соответственно множество точек входа в область Ф_ху и выхода из нее; а и b – абсциссы крайних точек области Ф_ху в направлении оси ОХ.

2. Последовательно вычислить:

а) внутренний интеграл 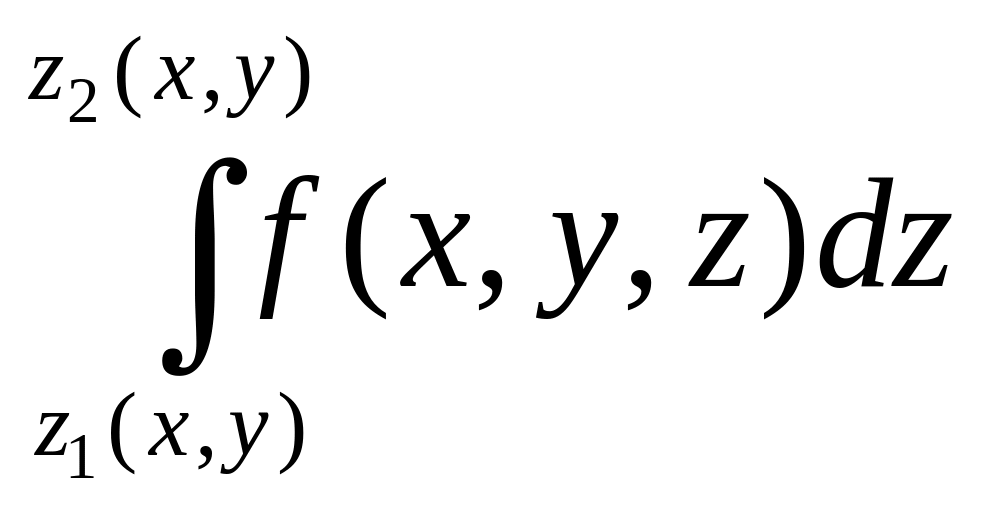, где z – переменная интегрирования; х и у считаются фиксированными; результатом вычислений является некоторая функция двух переменных F(х, у);

б) интеграл 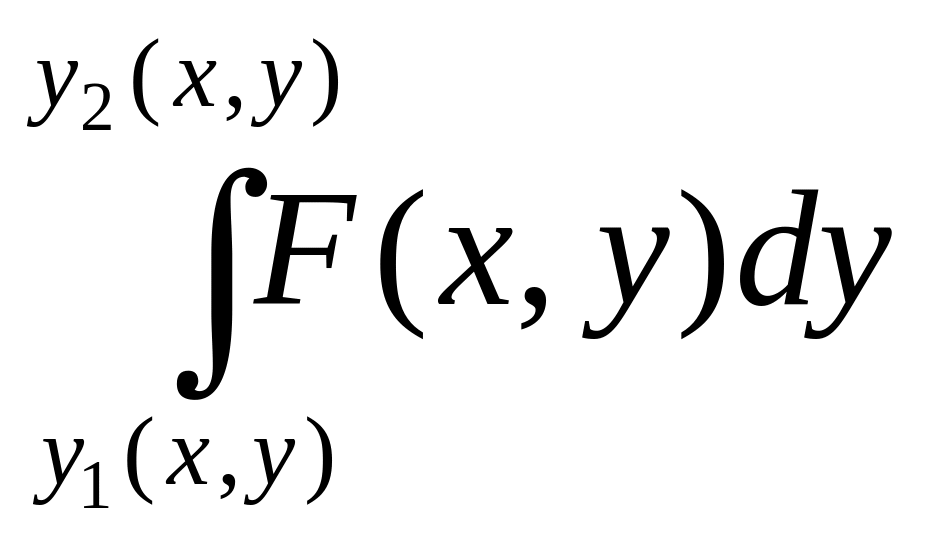, где у – переменная интегрирования, а х –считается фиксированным; результат вычисления – функция (х) одной переменной;

в) внешний интеграл , где х – переменная интегрирования. В результате получается некоторое действительное число.

Примеры решения задач/

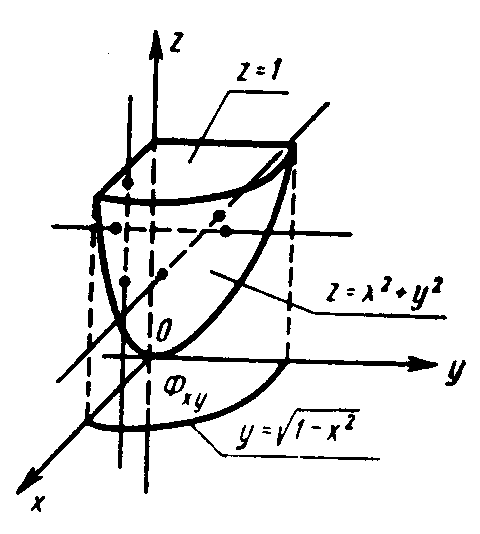
Задача 2.1. Вычислить , где область ограничена поверхностями z₁ = x² + y², х = 0, z = 0, z = 1.

Рис. 1.11

Решение. Условие выпуклости области Т выполнено. Составим выражение вида (2.7).Расставим пределы интегрирования: z=x²+y² – это множество точек входа в область Т, это поверхность параболоида вращения, а множество точек выхода из области Т плоскость z = 1, поэтому x²+y² z , x²+y²≤ z 1; множество точек входа в область Ф_ху есть прямая у =0, а множество выхода - дуга окружности у= , поэтому

0  у  ; пределы изменения по х: 0  х  1. Получим

= .

Вычислим повторный интеграл последовательно:

a) =xy[z²/2] =xy[0.5-(x²+y²)²/2]=

=(xy–x⁵y-2x³y³-xy⁵)/2;

б) 0.5 (xy–x⁵y–2x³y³–xy⁵)dy=

=[(xy²/2–x⁵y²/2–2x³y⁴/4–xy⁶/6)/2] =

=[x(1-x²)/2-x⁵(1-x²)/2-2x³(1-x²)²/4-x(1-x²)³/6]/2=(2x/3-x³+x⁷/3);

в) 0.5 (2x/3–x³+x⁷/3)dx=[(x²/3–x⁴/4+x⁸/24)/4] = /32.

Задача 2.2. Вычислить интеграл: ,

где V – тетраэдр, ограниченный координатными плоскостями и плоскостью 2х+2у+z–6=0.

Рис. 2.3

Решение. Тетраэдр, ограниченный снизу плоскостью z=0, сверху плоскостью z=6–2х–2у. Поэтому в области интегрирования V переменная z изменяется от z=0, до z=6–2х–2у (рис. 2.3).

Проекцией области V на плоскость ХОУ является треугольник ОАВ.Уравнение прямой АВ получим, решая совместно уравнения плоскостей:

Отсюда, уравнение прямой АВ имеет вид: х+у–3=0.

В области D_хоу переменная х изменяется в пределах 0 х 3, а переменная у изменяется 0 у 3–х.

Поэтому:

.

Вычислим внутренний интеграл в тройном интеграле

.

Следовательно:

.

Вычислим внутренний интеграл в двойном интеграле:

.

Получим

.

Ответ: .

Задачи для самостоятельного решения

Задача 2.3. Вычислить тройной интеграл:

,

где V – тело, ограниченное поверхностями у = x²; х = y²; z = xy; z = 0.

Указание.

.

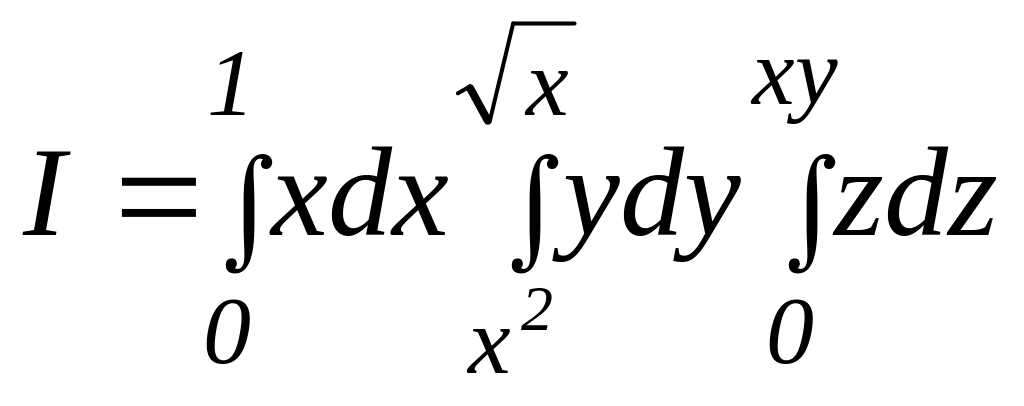Ответ: .

Задача 2.4. Вычислить тройной интеграл:

,

где V–пирамида, ограниченная плоскостями х=0, у=0, z=0, x+y+z=1.

Ответ: .

Задача 2.5. Вычислить тройной интеграл:

,

где V – тело, ограниченное параболоидом z = x² + y² и плоскостью z = 1.

Рис. 2.4

Указание. Проекцией поверхности V не плоскость ХОУ D_хоу является круг. Уравнение окружности, ограничивающей этот круг

х²+у²=1 (рис. 2.4). В области интегрирования переменная изменяется в пределах х²+у²  z  1.В области D_хоу переменная у изменяется от ее значения на нижней части окружности до значения на верхней части этой же окружности. Переменная х изменяется в пределах – 1  х  1.

По формуле (2.1) получим:

.

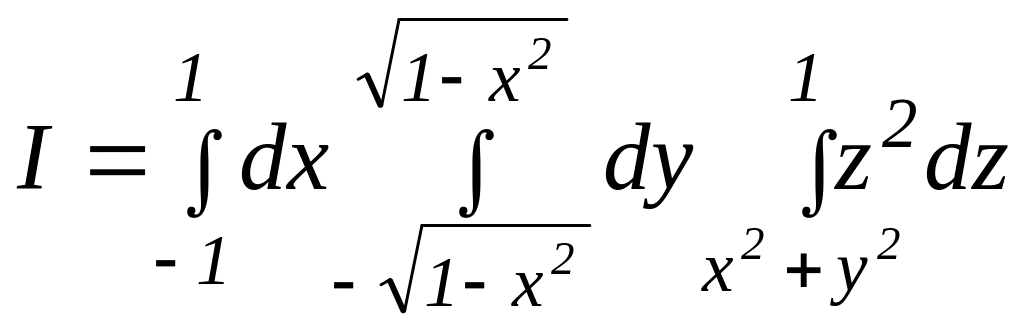Ответ: .