3. Криволинейные интегралы
3.1. Криволинейный интеграл первого рода
Определение криволинейного интеграла первого рода и его физический смысл
Рассмотрим задачу, которая естественным образом приводит к одному из обобщений понятия определенного интеграла - криволинейному интегралу первого рода. Эта физическая задача о вычислении массы материальной кривой.
Предположим, что на некоторой пространственной спрямляемой кривой АВ масса распределена непрерывно. Будем называть средней плотностью дуги этой материальной кривой отношение ее массы к длине участка, а плотностью материальной кривой в данной точке – предел средней плотности участка кривой, содержащего эту точку, при стягивании последнего к данной точке. Найдем массу материальной кривой АВ, если известна плотность кривой в каждой ее точке М, т.е. = (М) – заданная непрерывная функция от М.
Рис.
3.1
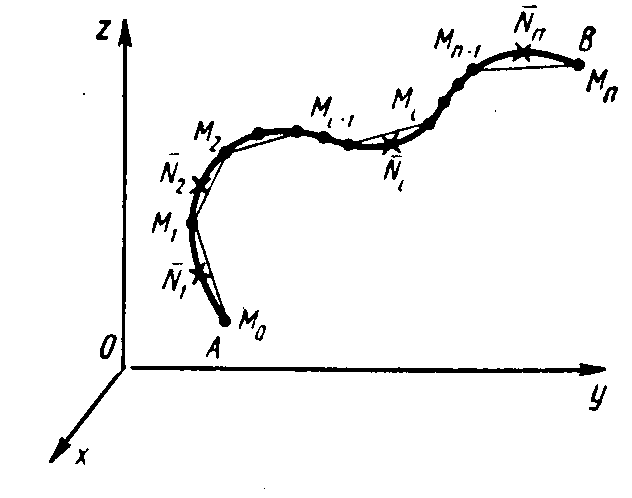
Рассмотрим произвольное разбиение {Mк}, (к = 0, 1, 2, …, n) кривой АВ с помощью n – точек, на n дуг M0M1, M1M2 , …, Mn-1Mn (рис. 3.1).
Наибольшую
из длин дуг разбиения кривой АВ
обозначим через d
и назовем диаметром этого разбиения.
При d
0 число дуг
неограниченно увеличивается. На каждой
из дуг Mк-1Mк
произвольно выберем точку
(
,
,
)
и вычислим в ней плотность к
= (
)
кривой. Если предположить, что плотность
во всех точках каждого элементарного
участка постоянна и равна ее значению
в точке
,
то масса каждой элементарной дуги mк
приближенно равна произведению (
)lк,
где lк
– длина
Mк-1Mк
дуги. Суммируя массы всех элементарных
дуг разбиения, получим приближенное
значение массы кривой АВ
m
mk
=
(
)lк
. (3.1)
Т.к. функция ( ) непрерывна, то чем «меньше» разбиение кривой АВ, тем точнее равенство (3.1).
За массу кривой АВ принимают предел правой части этого равенства при стремлении диаметра разбиения d к нулю, т.е.
m = ( )lк . (3.2)
К вычислению пределов сумм указанного вида сводится большое количество математических и прикладных задач. Поэтому отвлечемся от конкретного содержания задачи и последовательно повторим все операции, выполненные при составлении правой части равенства (3.2).
Рассмотрим в трехмерном пространстве OXYZ некоторую гладкую кривую АВ, в каждой точке задана функция f(x, y, z). Рассмотрим произвольно разбиение {Mк} кривой АВ с помощью n точек и выберем в каждой элементарной дуге разбиения точку ( , , ). Определим значения функции f в отмеченных точках и составим сумму
,
,
)
lк
.(3.3)
Сумма вида (3.3) называется интегральной суммой первого рода для функции f(x, y, z), заданной на кривой АВ, соответствующей разбиению {Mк} с отмеченными точками (к = 0, 1, 2, …, n). Пусть разбиение кривой АВ становится все более мелким, так что d 0, а число элементарных дуг неограниченно возрастает (n ).
Определение.
Если при d
0 (n
)
интегральная сумма (3.3) имеет конечный
предел J,
не зависящий от способа разбиения кривой
АВ
на частичные дуги и выбора точек
в каждой из них, то этот предел называется
криволинейным интегралом первого рода
(по длине дуги) от функции f(M)
= f(x,
y,
z)
по кривой АВ
и обозначается
(x,
y,
z)dl.
Таким образом:
(x,
y,
z)dl
=
,
,
)lк
.
(3.4)
Кривая АВ называется кривой интегрирования, точка А – начальной, а В – конечной точками интегрирования.
Замечание 1. Если кривая АВ лежит в плоскости ХОY и функция f не зависит от z, то криволинейный интеграл первого рода имеет вид
J = (x, y, z)dl.
Замечание 2. Из определения криволинейного интеграла первого рода следует, что он зависит от направления кривой АВ. В самом деле, длина дуги lк не зависит от того, какая из точек Mк-1 или Mк принята за начало, а какая за конец дуги. Поэтому
(x,
y, z)dl =
(x,
y, z)dl. (3.5)
Из формулы (3.2) следует, что масса m материальной кривой АВ, имеющей плотность (x, y, z), равна криволинейному интегралу от функции (x, y, z) по кривой АВ, т.е.
m
=
(x,
y,
z)
dl
(3.6)
В этом состоит физический смысл криволинейного интеграла первого рода.
Теорема. Если функция f(x, y, z) непрерывна (или кусочно-непрерывна и ограничена) вдоль кривой АВ, имеющей конечную длину, то криволинейный интеграл первого рода (x, y, z)dl существует.
Свойства криволинейных интегралов
первого рода
Перечислим основные свойства криволинейного интеграла первого рода, доказательство которых аналогично доказательству соответствующих свойств определенного интеграла:
1. Аддитивность. Если дуга АВ составлена из двух дуг АС и СВ и для f(x, y, z) существует криволинейный интеграл по дуге АВ, то для f(x, y, z) существуют криволинейные интегралы по АС и СВ, причем
(x,
y, z)dl
=
(x,
y, z)dl +
(x,
y, z)dl . (3.7)
2. Линейность. Если для функций f1(x, y, z) и f2(x, y, z) существуют криволинейные интегралы по дуге АВ, то для функции c1f1(x, y, z) + c2f2(x, y, z) также существует криволинейный интеграл по дуге АВ, причем:
c1f1(x,y,z)+c2f2(x,y,z)]dl=c1
x,y,z)]dl+c2
x,y,z)]dl,(3.8)
где c1 и c2 – вещественные числа.
Частными случаями формулы (3.8) являются формулы
f1(x, y, z) + f2(x, y, z)]dl = x, y, z)]dl + x, y, z)]dl ,
f(x,
y, z)dl = c
(x,
y, z)dl.
3. Если в точках кривой АВ всюду выполняется неравенство
f1(x, y, z) f2(x, y, z), то
x, y, z)]dl x, y, z)]dl . (3.9)
4. Оценка абсолютной величины интеграла. Если существует криволинейный интеграл по дуге АВ от функции
f(x,y, z), то существует и криволинейный интеграл по дуге АВ от функции f(x, y, z) , причем
.
(3.10)
5. Теорема о среднем значении. Если функция f(x, y, z) непрерывна вдоль дуги АВ, то на этой дуге найдется такая точка Q, в которой
(x, y, z)dl = f(Q) ,(3.11)
где – длина дуги АВ.
6. Если функция f(x, y, z) непрерывна на кривой АВ, имеющей длину , то
m (x, y, z)dl M
где m и M – наименьшие и наибольшие значения функции
f(x, y, z) на АВ.
Замечание. В случае, когда кривая интегрирования
Г
– замкнутая кривая, т.е. когда точка В
совпадает
с точкой А,
то интеграл по замкнутой кривой обозначают
(x,
y,
z)dl.
Для криволинейного интеграла первого рода по замкнутым кривым свойства остаются те же, что и по незамкнутым кривым.
Вычисление криволинейного интеграла первого рода
Вычисление криволинейного интеграла (x, y)dl сводится к вычислению некоторого определенного интеграла.
Пусть
плоская кривая АВ
задана параметрическими уравнениями
вида: x
= x(t),
y
= y(t),
причем существуют непрерывные производные
и
,
где параметр t
изменяется в пределах
t
.
Установим по кривой АВ
направление
движения от точки А,
которой соответствует значение параметра
t
=
, к точке В,
которой соответствует t
= .
Тогда
известно, что dl
=
,
криволинейный интеграл выражается
через определенный интеграл по формуле
(x,
y, z)dl =
[x(t),
y(t)]
(3.12)
В частности, если гладкая кривая АВ задана явным уравнением y = y(x), где x , то
(x,
y)dl =
[x,
y(x)]
.
(3.13)
Рассмотрим
теперь случай пространственной кривой
АВ. Пусть параметрические уравнения
пространственной гладкой кривой АВ
имеют вид x = x(t),
y = y(t),
z = z(t),
причем существуют непрерывные производные
,
,
.
предположим, что параметр t изменяется в пределах
t ( < ). Тогда справедлива формула
(x,
y, z)dl =
[x(t),
y(t), z(t)]
.
(3.14)
Замечание: Криволинейный интеграл от функции f(x, y) по дуге АВ, заданной уравнением в полярных координатах r = r(), где 1 2 вычисляется с помощью формулы
(x,
y)dl =
(rcos,
rsin)
.
(3.15)
Задача 3.1.
Вычислить
dl
по дуге плоской кривой
y = lnx, где 1 x 2.
Решение. Используя формулу (3.13), получим:
dl
=
dx
=
1+x2
d(1 + x2)
=
=
(1+
x2
=
.
Задача 3.2.
Вычислить
x
+ y + z)
dl по дуге витка
винтовой линии, заданной параметрическими
уравнениями
x = cos t, y =
sin t, z = t при 0
t
.
Решение. По формуле (3.14), находим:
x
+ y + z)dl
=
cost
+ sint + t)
dt
=
=
cost+sint+t)dt=
(sint
– cost+
)
=
(2
+
).