2.4. Применение кратных интегралов в задачах механики и физики

Приложения двойных интегралов

Рассмотрим на плоскости XOY материальную пластинку, т.е. некоторую область D, по которой распределена масса с плотностью (x, y), где (x, y) – непрерывная функция. Тогда, как мы уже знаем, масса на всей плоскости определяется по формуле

m = . (2.21)

Известно, что момент инерции системы материальных точек М₁, М₂,… M_n с массами m₁, m₂, …m_n, относительно некоторой точки О есть сумма моментов инерции отдельных точек системы J = ,где r² – расстояние от точки до точки О.

Пусть фигура D расположена в плоскости XOY. Тогда можно доказать, что момент инерции этой фигуры относительно начала координат J₀, в предположении что поверхностная плотность равна (x, y), вычисляется по формуле

J₀ = , (2.22)

а интегралы

J_x = ; (2.23)

J_y = (2.24)

называются соответственно моментами инерции фигуры D относительно осей OX и OY, т.е. J₀ = J_x + J_y .

Известно, что координаты центра масс системы материальных точек М₁, М₂,… M_n с массами m₁, m₂, …m_n определяются по формулам

x_c = ; y_c = .

Учитывая эти формулы, можно доказать, что коэффициенты центра масс плоской фигуры D, имеющей поверхностную плоскость (x, y), вычисляются по формулам

x_c = = ; y_c = = , (2.25)

где выражение

M_y = , M_x = (2.26)

называются статическими моментами плоской фигуры D относительно осей OY и OX.

Задача 2.12. Найти координаты центра масс однородной пластины, ограниченной параболой y = 4 – x² и осью ОХ

(рис. 2.10).

Решение. Так как фигура симметрична относительно оси OY, то без вычислений ясно, что x_c = 0. Ординату y_c посчитаем по формуле (1.60), т.к. пластинка однородна, то

(x, y) = сonst, поэтому y_c = = ,

где S_D = - площадь области D.

Получим

S_D = = = 32/3,M_x = = =

= = = = .

y

-2 2 x

Рис. 2.10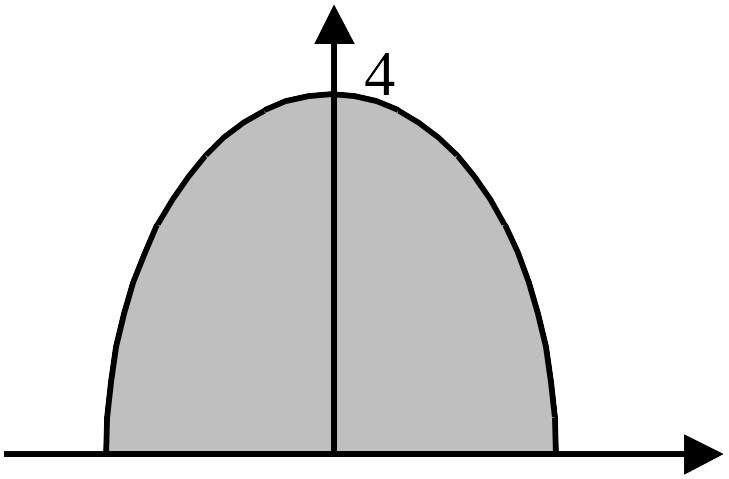

Следовательно , y_c = 8/5.

Итак, координаты центра масс равны: x_c = 0, y_c =8/5.

Приложения тройных интегралов

Как было показано ранее, объем V пространственного тела Т вычисляется по формулам V= dydz - в прямоугольных координатах;

V = drdd - в цилиндрических координатах;

V = φdrdd - в сферических координатах.

Если дано некоторое тело Т с объемной плотностью (M) = (x, y, z), представляющей собой непрерывную функцию, то масса m этого тела вычисляется по формуле

m = .

Координаты центра масс x_c, y_c, z_c некоторого пространственного тела, имеющего объемную плотность (M) = (x, y, z) выражаются формулами

x_c = , y_c = ,

z_c = .

В частности, если рассматриваемое тело однородно, т.е. (M) = const, тогда выражение для координат центра масс принимает более простой вид

x_c = , y_c = , z_c = ,

где V – объем данного тела Т.

Моменты инерции пространственного тела с объемной плотностью

(M) = (x, y, z) относительно координатных осей определяется по формулам

J_x = , J_y = , J_z = .

Для момента инерции относительно начала координат формула имеет вид

J₀ = .

Момент инерции относительно координатных плоскостей вычисляются по формулам

J_xy = , J_yz = ,

J_xz = .

Статические моменты относительно координатных плоскостей равны

M_xy = , M_yz = ,

M_xz = .

б) Вычисление массы тела

Если дано некоторое тело с объемной плотностью  (х, у, z), представляющий собой непрерывную функцию, то масса m этого тела, равна тройному интегралу от функции плотности  (х, у, z), распространенному на объем V, занимаемый этим телом:

. (2.27)

Задача 2.13. Вычислить массу тела, ограниченного сферой х²+у²+z² = 4 и параболоидом х²+у² = 3z, если плотность в каждой точке тела равна аппликате точки (т.е.  = z)

Решение.

В этой задаче удобно перейти к цилиндрическим координатам, так как в уравнении параболоида содержится сумма х²+у², а в цилиндрических координатах х²+у² = r².

Запишем уравнения поверхностей, ограничивающих тело, в цилиндрических координатах.

Уравнение сферы примет вид: r²+z² = 4; r² =4–z².

Уравнение параболоида: r² = 3z.

Из этих уравнений следует, что на параболоиде: z=r²/3, а на сфере .

Спроектируем это тело на плоскость ХОУ. Проекцией будет круг. Найдем радиус этого круга. Для этого определим, при каком значении z пересекаются поверхности, т.е. определим z из системы:

;

Получим z² + 3z – 4 = 0; z₁ = 1; z₂ = – 4.

Смыслу задачи удовлетворяет только z = 1.

Подставим это значение в любое из уравнений системы, получим r² = 3, .

Итак, радиус круга, в который проектировалось тело равен ; переменные r,, z в теле изменяются в пределах:

0  r  , 0    2 , .

Масса тела вычисляется по формуле (2.27), в которой элемент объема .

Таким образом,

.

Ответ: .

Задача 2.14. Вычислить массу тела, ограниченного сферой х²+у²+z² = 4 и параболоидом х²+у² = 3z, если плотность в каждой точке тела равна аппликате точки (т.е.  = z)

Решение.

В этой задаче удобно перейти к цилиндрическим координатам, так как в уравнении параболоида содержится сумма х²+у², а в цилиндрических координатах х²+у² = r².

Запишем уравнения поверхностей, ограничивающих тело, в цилиндрических координатах.

Уравнение сферы примет вид:

r² + z² = 4; r² = 4 – z².

Уравнение параболоида: r² = 3z.

Из этих уравнений следует, что на параболоиде: z=r²/3, а на сфере .

Спроектируем это тело на плоскость ХОУ. Проекцией будет круг. Найдем радиус этого круга. Для этого определим, при каком значении z пересекаются поверхности, т.е. определим z из системы:

;

Получим z² + 3z – 4 = 0; z₁ = 1; z₂ = – 4.

Смыслу задачи удовлетворяет только z = 1.

Подставим это значение в любое из уравнений системы, получим r² = 3, .

Итак, радиус круга, в который проектировалось тело равен ; переменные r,, z в теле изменяются в пределах:

0  r  , 0    2 , .

Масса тела вычисляется по формуле (2.27), в которой элемент объема .

Таким образом,

.

Ответ: .

Задача 2.15. Определить момент инерции относительно оси OZ однородной пирамиды Т с плотностью, ограниченной плотностями x = 0, y = 0, x+ y+ z= 1 (рис. 2.11).

Рис. 2.11

Рис. 1.24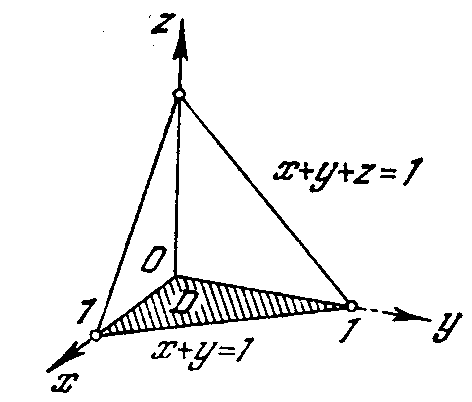

Решение. Согласно формуле

J_z= =3 = =3 =3 .

Задачи для самостоятельного решения

Задача 2.16. Найти координаты центра тяжести однородных пластин, ограниченных кривыми

Задача 2.17. Вычислить массу тела, ограниченного сферой х²+у²+z²= 1, если в каждой точке тела плотность равна квадрату ее расстояния от начала координат.

Указание. Квадрат расстояния точки от начала координат равен сумме: х²+у²+z², координат этой точки, поэтому

(х, у, z) = х²+у²+z²; и масса тела равна:

,

так как тело ограничено сферой, то удобно перейти к сферическим координатам, по формулам (2.19), (2.20).

Получим,

,

где 0    1, 0    2, 0    2 .

Ответ: .

Задача 2.18. Вычислить массу пирамиды, ограниченной плоскостями х + у + z = 1, х = 0, у = 0, z = 0, если плотность ее в текущей точке тела М(х, у, z) равна  = хуz.

Ответ: .

Задача 2.19. Найти массу однородного тела (плотность в каждой его точке  = const), ограниченного поверхностями

а) z = 2–x–y, а²+у²= 1, х = 0, у = 0, z = 0.

б) ; х²+у²= 2х, z = 0.

Ответ: а) , б) .

Задача 2.20. Найти моменты инерции относительно осей Ox и Oy фигур, ограниченных кривыми, заданными уравнениями: а) 2x + y=1, 3x + y = 1, y = 0;

b) xy = 1, xy = 2, x = 2y, 2x = y (x > 0, y> 0 ).

Задача 2.21. Найти координаты центра тяжести однородных пластин, ограниченных кривыми

y² = 4x+ 4, y² = -2x+ 4; y = x², x + y=3, y = 0;

Задача 2.22. Найти координаты центра тяжести однородных тел, ограниченных поверхностями:

a) x² + y² = z²/4 , z=2; b) z = x² + y² , x + y = 1, x = 0, y = 0, z=0;

с) x²/4 + y²/9 + z² = 1, x = 0, y = 0, z = 0.