3.4. Формула Грина. Вычисление площадей с помощью криволинейного интеграла второго рода

Криволинейный интеграл по простому замкнутому гладкому контуру L, ограничивающему односвязную область D может быть преобразован в некоторый двойной интеграл по области D, ограниченной этим контуром.

Это преобразование выполняется по формуле Грина, которая имеет вид:

. (3.32)

Предполагается, что функции Р(х, у) и Q(x, y), а также их частные производные непрерывны в области D и на контуре L, который ее ограничивает, причем, контур L, пробегается в положительном направлении, т.е. так, что область D остается слева.

Если формулу Грина прочесть справа налево, то можно сказать, что она сводит вычисление двойного интеграла по области D к вычислению криволинейного интеграла взятого по контуру L, ограничивающему эту область.

Формула (3.32) справедлива не только для области D указанного вида, но и для более сложных областей, ограниченных несколькими простыми гладкими контурами. В случае:

,

следует рассматривать как сумму интегралов по составляющим контурам, причем, интегрирование по этим контурам должно вестись в таком направлении, чтобы область D оставалась слева.

Многие криволинейные интегралы, взятые по замкнутому контуру, удобно вычислять, сводя их к двойному.

Задача 3.19. Вычислить, применяя формулу Грина, интеграл.

,

где L – окружность х² + у² = а², пробегаемая в положительном направлении.

Решение. Здесь Р(х, у) = - х² у; Q(х, у) = - х у²;

; .

Подставляя эти значения в формулу (3.17), получим:

,

где D – круг, ограниченный окружностью х² + у² = а². Вычисление полученного интеграла удобно провести в полярных координатах, при этом элемент площади dxdy = rdrd,

а х² + у² = r².

Получим

.

Ответ: .

Задачи для самостоятельного решения

Задача 3.20. С помощью формулы Грина вычислить интеграл

, где

С – замкнутый контур, составленный дугами двух окружностей х² + у² = 1 и х² + у² = 4 (y > 0) и отрезками прямых у = х и (у  0), заключенных между этими окружностями (рис. 3.3).

Рис. 3.3

Указание. Найти .

; ;

.

По формуле Грина интеграл равен: .

В данной задаче перейдем к полярным координатам

.

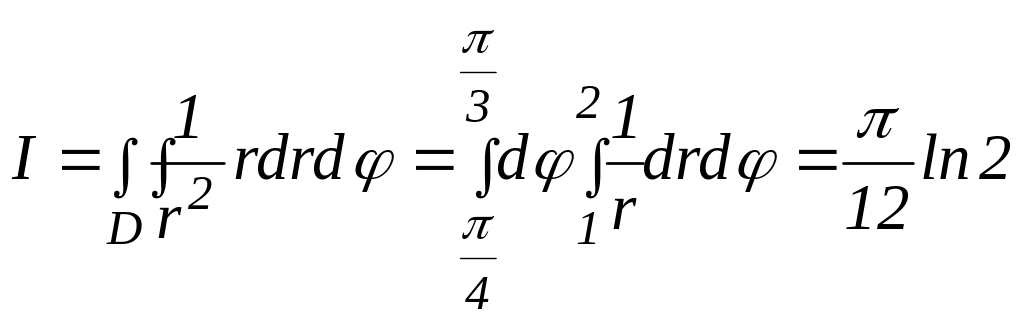Ответ: .

Задача 3.21. Криволинейный интеграл из предыдущей задачи и по тому же контуру вычислить, не прибегая к формуле Грина.

Указание. Уравнения окружности преобразовать к параметрической форме. Получим уравнение:

и

Параметр t на дуге ВС изменяется от до , ,

а на дуге DА от до . Интегралы по этим двум дугам взаимно уничтожаются. Перемещая х на отрезке АВ применяется от , а на отрезке СD от 1 до 1/2.

С помощью интеграла второго рода, площадь плоской фигуры, ограниченной кусочно-гладкой кривой вычисляется, по формуле:

, (3.33)

где L – контур, ограничивающий искомую площадь, а интегрирование по этому контуру ведется в положительном направлении, т.е. чтобы область D оставалась слева.

Для вычисления площади с помощью криволинейного интеграла применяются такие формулы:

; (3.34)

. (3.35)

Задача 3.22. С помощью криволинейного интеграла, вычислить площадь, ограниченную эллипсом:

(0  t  2).

Решение. Найдем: dx = - a  sin t dt, dy= b  cos t dt.

Подынтегральное выражение по этой формуле равно:

x dy – y dx = (ab cos² t + ab sin² t)dt = a  b  dt.

Получим:

(кв. ед.).

Ответ: (кв.ед.).

Задача 3.23. Определить площадь, ограниченную одной аркой циклоиды (рис. 3.4).

(0  t  2).

Рис. 3.4

Решение. Найдем dx = a(1–cost)dt, dy = a sin t dt.

Тогда, подынтегральное выражение примет вид:

x dy–y dx=a(t–sint)a sint dt–a(1–cost)a(1–cost) dt=

= a²(t sint + 2cost – 2)dt.

Интегрирование ведется по контуру ОАВО в направлении, указанном стрелками. На отрезке ОА у = 0 и dу = 0. Поэтому на этом отрезке подынтегральное выражение примет вид: x dy–y dx = 0. На дуге АВО периметр t изменяется от 2 до 0. Учитывая это, получим:

Ответ: S = 3 a² (кв. ед.).

Задачи для самостоятельного решения

Задача 3.24. Определить площадь, ограниченную астроидой:

(0  t  2).

Ответ: .

Задача 3.25. Найти площадь, ограниченную кардиоидой:

(0  t  2).

Ответ: S = 6 a² (кв. ед.).