3.3. Условия независимости криволинейного интеграла от пути интегрирования

Если функции Р(х,у) и Q(x,y) определены и непрерывны вместе со своими частными производными и в замкнутой ограниченной односвязной областью D, то для того, чтобы в криволинейный интеграл

не зависел от формы пути интегрирования, необходимо и достаточно, чтобы во всех точках этой области выполнялось условие

= . (3.30)

Но условие (3.30) является необходимым и достаточным для того, чтобы выражение Р(х,у)dx + Q(x,y)dy, являлось полным дифференциалом некоторой функции. Поэтому можно утверждать, что для того, чтобы криволинейный интеграл не зависел от пути интегрирования АВ, а зависел только от его концов и достаточно, чтобы подынтегральное выражение Рdx + Qdy, было полным дифференциалом некоторой функции.

Но, если выполняются условия (3.30) и выражение Рdx + Qdy, является полным дифференциалом некоторой функции, то криволинейный интеграл (х,у)dx + Q(x,y)dy, взятый по любому замкнутому контуру L целиком лежащему в односвязной ограниченной замкнутой области D равен 0.

Если путь, по которому вычисляется криволинейный интеграл, безразличен, то употребляется обозначение:

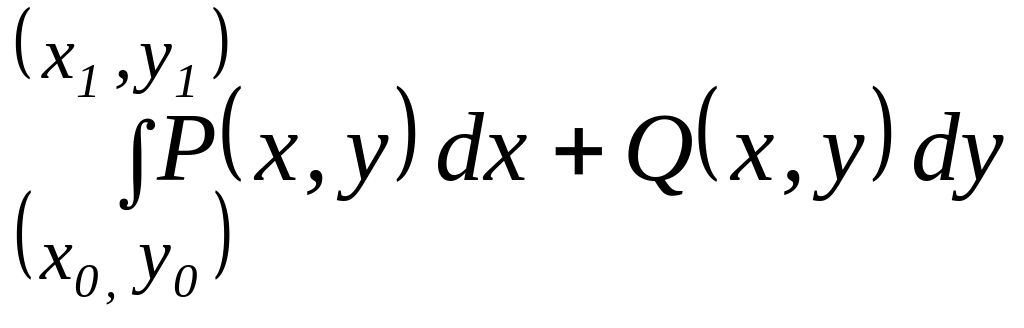(3.31),

где (х₀, у₀) и (х₁, у₁) – координаты начала и конца пути интегрирования.

Задача 3.13. Выяснить, будет ли криволинейный интеграл зависеть от формы пути интегрирования:

.

Решение. Здесь Р(х, у) = 6ху + 4у² + 5у,

а функция Q(x,y) = 3x² + 8xy + 5x. Интеграл не будет зависеть от пути интегрирования, если выполнено условия (3.30).

; ,

Следовательно, , и криволинейный интеграл зависит от формы пути интегрирования.

Задача 3.14. Убедится, что интеграл

не зависит от формы пути интегрирования, и после этого вычислить его по отрезку прямой, соединяющей точки (2, 3) и (3, 4).

Решение. Р(х, у) = 6ху² + 4х³ , Q(x,y) = 6x²y + 3у².

; , т.е. .

Интеграл не будет зависеть от пути интегрирования.

Уравнение прямой, соединяющий точки с координатами (2, 3) и (3, 4) имеет вид: у = х + 1; dy = dx.

Получим:

.

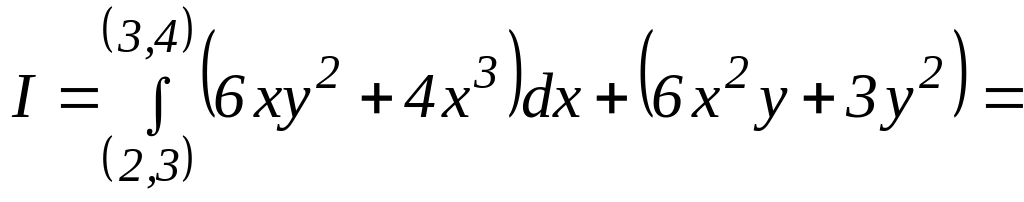
Ответ: 426.

Задача 3.15. Будет ли криволинейный интеграл,

,

взятый по замкнутому контуру L равен 0 ?

Решение: При выполнении условия

(где Р(х, у) = , Q(х, у) = ).

Криволинейный интеграл, взятый по любому замкнутому контуру, будет равен нулю. Поэтому, чтобы ответить на вопрос, вычислим:

, , т.е. .

Так как функции выражение Р(х,у) и Q(x,y) и их частные производные и имеют разрыв при х = 0, следует указать, что заданный интеграл, взятый по любому замкнутому контуру, будет равен нулю, но этот контур не должен проходить через точку с абсциссой х = 0.

Задачи для самостоятельного решения

Задача 3.16. Вычислить интеграл

.

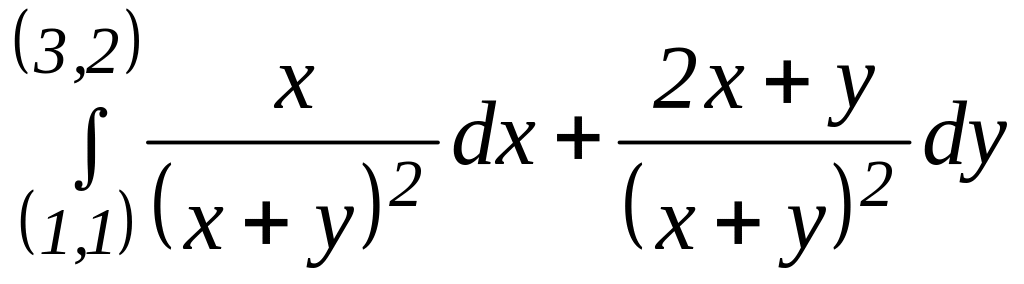Указание. Убедится, что . За путь интегрирования выбрать прямую, соединяющие точки (1, 1) и (3, 2). Ее уравнение .

Ответ: .

Задача 3.17. Будет ли криволинейный интеграл

по любому замкнутому контуру, будет равен нулю. Подтвердить полученное заключение непосредственным вычислением, по какому-нибудь замкнутому контуру.

Указание. Проверить, является ли подынтегральное выражение полным дифференциалом, для этого найти и , где Р(х,у)=х³+ху²; Q(х,у)=х²у+у³, так как ,

то можно утвердительно ответить на вопрос задачи.

Выбрать в качестве замкнутого контура, например, окружность единичного радиуса с центром в начале координат. Параметрические уравнения такой окружности имеют вид:

(0  t  2).

Задача 3.18. Убедившись, что подынтегральное выражение является полным дифференциалом, вычислить следующие интегралы:

1)

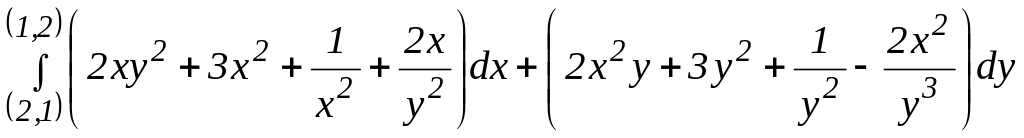
(вдоль путей, не пересекающих координатных осей и не проходящих через начале координат).

2) ;

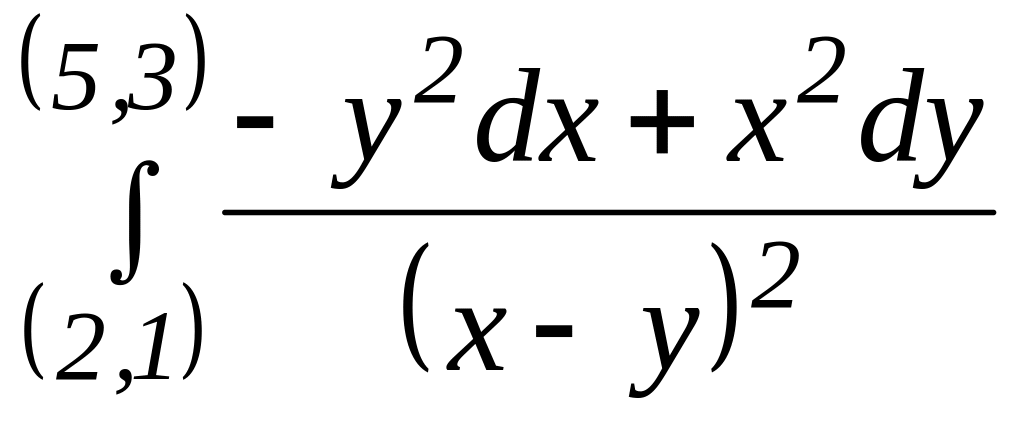(вдоль путей, которые не пересекают биссектрису первого и третьего координатных углов).

Ответ: 1) ; 2) 5,5.