ГОУВПО «Воронежский государственный технический

университет »

СПРАВОЧНИК МАГНИТНОГО ДИСКА

(Кафедра высшей математики

и физико-математического моделирования)

А.А. Катрахова В.С. Купцов А.В. Купцов

Кратные интегралы. Векторный анализ

Учебное пособие

Кратн. интегр. doc 5,38 Mb 14.03.2011 9,4 уч.-изд. л.

ГОУВПО «Воронежский государственный

технический университет »

А.А. Катрахова В.С. Купцов А.В. Купцов

Кратные интегралы. Векторный анализ

Утверждено Редакционно-издательским советом

университета в качестве учебного пособия

Воронеж 2011

УДК 517.53

Катрахова А.А. Кратные интегралы. Векторный анализ: учеб. пособие / А.А. Катрахова, В.С. Купцов, А.В. Купцов. Воронеж: ГОУ ВПО «Воронежский государственный технический университет», 2011. -167 c.

Учебное пособие состоит из шести глав: в первых главах излагаются основы теории кратных интегралов, а в последних – элементы векторного анализа. Приводятся образцы решения задач и упражнения в виде примеров и задач.

Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования для студентов специальностей 220201 « Управление и информатика в технических системах», 140604 «Электропривод и автоматика промышленных установок и технологических комплексов», 140601 «Электромеханика», 110302 «Электрификация и автоматизация сельского хозяйства», дисциплине «Математика».

учебное пособие предназначено для студентов очной формы обучения.

Учебное пособие подготовлено в электронном виде в текстовом редакторе MS Word и содержится в файле

«Кратн. интегр. doc»

Табл. 1. Ил. 52. Библиогр.: 8 назв.

Рецензенты: кафедра дифференциальных уравнений

Воронежского государственного университета

(зав. кафедрой д-р физ.- мат. наук,

проф. А.И. Шашкин);

д-р физ.-мат. наук, проф. В.Г. Задорожний

 Катрахова А.А., Купцов В.С., Купцов А.В., 2011

 Оформление. ГОУВПО «Воронежский

государственный технический университет», 2011

Введение

Настоящее учебное пособие содержит изложение

теоретического материала по разделам «Кратные, криволинейные и поверхностные интегралы. Векторный анализ». Настоящее учебное пособие содержит также разбор и подробное решение типовых задач по разделам кратные, криволинейные и поверхностные интегралы и векторный анализ. Содержание пособия соответствует программе курса математики для студентов инженерно-технических специальностей вузов рассчитанной на 600 часов и утвержденной Министерством образования Российской Федерации в соответствии с новыми образовательными стандартами.

Каждому практическому занятию предпосылается конспективное изложение основных сведений из теории, справочные данные и формулы, относящиеся к соответствующему разделу. После подробного разбора типовых задач различной степени трудности помещены задачи для самостоятельного решения, которые в нужных случаях снабжены указаниями и ответами. Некоторые задачи решены различными способами. Такое построение пособия предоставляет студентам широкие возможности для активного самостоятельного изучения практической части курса математики.

В пособии дано систематическое изложение соответствующих разделов курса высшей математики на достаточном для вуза уровне, разобраны примеры, приведены упражнения для самостоятельного решения.

При изложении теории кратных, криволинейных и поверхностных интегралов подчеркивается едино образность определений, вводимых понятий как пределов соответствующих сумм, а также рассматриваются физические задачи, приводящие к определениям этих понятий.

Многие определения, теоремы и формулы сопровождаются комментариями, позволяющими более подробно раскрыть содержание вводимых понятий, смысл теорем и формул, связь излагаемого материала с предшествующим материалом и указать пути возможного применения, соответствующих теорем и формул при изучении последующих дисциплин. Это обстоятельство делает пособие удобным для самостоятельного изучения курса математики и студентами заочниками.

Обратимся подробнее к истории математики, чтобы ответить на вопрос о том, кто и когда доказал основные теоремы и формулы, ввел понятия, которые являются фундаментальными в указанных разделах.

В этом ряду великих математиков следует первым отметить выдающегося русского математика первой половины девятнадцатого века Михаила Васильевича Остроградского (1801-1862 гг.). Он учился в Харьковском университете, затем отправился в Париж (1822-1828 гг.), где познакомился с последними достижениями анализа. В курсе анализа мы встречаем «формулу Остроградского» для преобразования интеграла по объему в интеграл по поверхности, так называемую формулу Остроградского-Гаусса. Остроградский дал ее обобщение и на область любого числа измерений. Примерно одновременно с Якоби Остроградский дал первый вывод правила замены переменных в кратных интегралах.

На месте раздела между математикой восемнадцатого и девятнадцатого столетий возвышается величественная фигура Карла Фридриха Гаусса (1777-1855 гг.). Он родился в немецком городе Брауншвейге, учился в Геттингене, получил степень доктора и вплоть до конца своей жизни работал в качестве директора астрономической обсерватории. Выполняя большую работу по земному магнетизму, он положил начало развития теории потенциала как отдельной ветви математики с использованием интегралов по объему, причем были введены некоторые минимальные принципы.

Сын мельника из Нотингема и самоучка Джордж Грин (1793-1891 гг.) внимательно следил за новыми открытиями в области электричества. Результатом наблюдений работы стала книга «Опыт применения математического анализа к теории электричества и магнетизма». Гаусс не знал в это время работы Грина, но они оказались очень близки в названии терминов: «потенциальная функция» - это понятие ввел Грин, почти такой же термин «потенциал» выбрал Гаусс для обозначения решения уравнения Лапласа.

Два типа тождества между двойным и криволинейным интегралом, поверхностным и криволинейным интегралом носят название формул Грина, Стокса (1819-1903 гг.).

Терминами «оператор Гамильтона», функция Гамильтона мы обязаны Вильяму Роуэну Гамильтону (1805-1865 гг.), который родился в ирландской семье в Дублине, окончил колледж и был королевским астрономом вплоть до своей смерти. Гамильтон пытался проникнуть в алгебру числовых троек, числовых четверок и т.д. Он открыл кватернионы. Наиболее известной частью этого исчисления кватернионов является теория векторов.

Сейчас мы видим в векторах Гамильтона частный случай тензорной алгебры. Благодаря Гамильтону векторный анализ стал независимой ветвью математики, которая имеет широкие применения в настоящее время.

1. КратНые интегралы

1.1. Двойной интеграл, его свойства.

Геометрический и физический смысл

двойного интеграла

Рассмотрим на плоскости область Ф, ограниченную замкнутой гладкой (или кусочно-гладкой) кривой  (рис. 1.1). В дальнейшем всякое ограниченное замкнутое множество будем называть компактным множеством (или компактом). Диаметром компактной фигуры называется точная верхняя грань расстояний между двумя любыми точками этой фигуры. Геометрический диаметр компактной фигуры представляет собой наибольшую из ее хорд.

Если диаметр компактной фигуры стремится к нулю, то фигура стягивается в точку. Для рассмотренного компакта Ф на плоскости можно указать пару многоугольников А и В с площадями S(A) и S(B), из которых один содержится в Ф, а другой содержит Ф, т.е. A  Ф  B. Таких пар многоугольников можно подобрать бесконечное множество. Обозначим

= sup {S(A)} - точную верхнюю границу, а = inf {S(A)} – точную нижнюю грань этих множеств.

Определение 1. Если = = S, то число S называется площадью фигуры Ф, а сама фигура Ф называется квадрируемой.

Определение 2. Разбиением {Ф_к} квадратируемой фигуры Ф называется такая совокупность квадратируемых фигур Ф_к, объединение которых составляет фигуру Ф, причем никакие две различные фигуры Ф_к и Ф_l не имеют общих внутренних точек (т.е. Ф_к  Ф_l = 0, при к  l), {Ф_к} – сокращенная запись совокупности {Ф₁, Ф₂ …, Ф_n}.

Определение 3. Наибольший из диаметров фигур, составляющих разбиение, называют диаметром разбиения {Ф_к} и обозначают его через d.

Пусть на плоской компактной фигуре Ф задана функция f:Ф  R. Для определения двойного интеграла (по Риману) от функции f по фигуре Ф рассмотрим разбиение {Ф_к} области Ф (рис. 1.1). Это разбиение должно быть таким, чтобы все геометрические фигуры Ф_к были квадрируемыми, т.е. имели бы площади, которые обозначим через S_к.

В каждой геометрической фигуре Ф разбиения {Ф_к} выберем произвольную точку) ( )  Ф_к.

Если диаметр d разбиения фигуры Ф стремится к нулю, то число n фигур неограниченно увеличивается, т.е. n  . Вычислим значения функции f( ) и составим сумму произведений вида

J_n = S_к. (1.1)

Рис.1.1

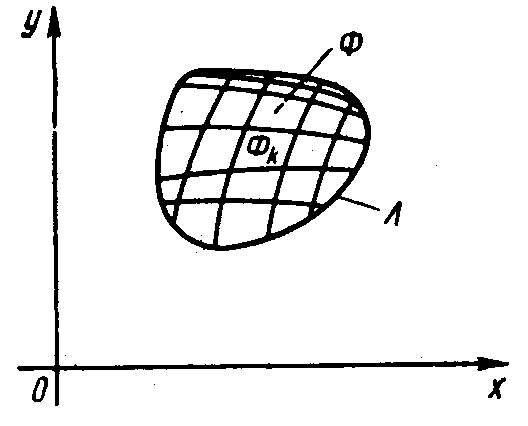
Сумма вида (1.1) называется двумерной интегральной суммой Римана функции f(x,y), соответствующей разбиению {Ф_к} с отмеченными точками ( ), к = 1,2,…, n.

Определение 4. Число J называется пределом последовательности интегральных сумм (1.1) при d  0, если для любого числа  > 0 существует такое число  > 0, что при d <  независимо от выбора отмеченных точек ( ) в частичных фигурах Ф_к выполняется неравенство /J_n - J/ < .

Определение 5. Предел последовательности двумерных интегральных сумм вида (1.1) при d  0 (если он существует) называется двойным интегралом (по Риману) от функции f(x, y) по области Ф и обозначается

= S_к. (1.2)

В этом случае функция f(x, y) называется интегрируемой (по Риману) в области Ф. Переменные x и y являются переменными интегрирования; f(x,y) - подынтегральной функцией; f(x, y)dS - подынтегральным выражением; dS - двумерным элементом площади; Ф - областью интегрирования.

Замечание. Имеется глубокая аналогия двух понятий – определенного и двойного интегралов. В обоих случаях рассматривают некоторую функцию: в первом случае одной действительной переменной f(x), определенную на отрезке [a, b]  R. Во втором – функцию двух переменных f(x, y), определенную на плоской фигуре Ф  R². В том и другом случае область определения разбивают на части и выбирают произвольно отмеченные точки, в которых вычисляют значение функции f. Затем вычисленные значения функций умножают на меру соответствующих частей. В первом случае такой мерой служит длина отрезка [x_к, x_к+1]. Во втором – S_к площадь части Ф_к. Наконец, в том и в другом случае составляют интегральные суммы Римана, соответствующие разбиениям с отмеченными в них точками и находят их пределы при стремлении к нулю диаметра разбиения. В случае так называемого прямоугольного разбиения области Ф, образованного прямыми, параллельными осям координат OX и OY, частичные фигуры Ф_кj представляют собой прямоугольники со сторонами, длины которых равны x_к , y_j (за исключением фигур, примыкающих к границе ). Чтобы подчеркнуть, что разбиение является прямоугольным в формуле (1.2) положим dS = dxdy.

Тогда

= x_кy_j, (1.3)

где ( )  Ф_кj и суммирование в равенстве (1.3) распространяется на все значения к и j, для которых S_кj = x_кy_j. Можно доказать, что непрямоугольные фигуры, примыкающие к границе , не влияют на значение предела (1.3). Выражение dxdy называется двумерным элементом площади в декартовых прямоугольных координатах.

Геометрический и физический

смысл двойного интеграла

Рассмотрим цилиндроид Т, т.е. тело Т R³, ограниченное сверху поверхностью z = f(x, y), снизу плоскостью z = 0, сбоку – цилиндрической поверхностью, направляющей которой служит гладкая граница  компактной фигуры Ф, а образующими, являются прямые, параллельные оси OZ (рис. 1.2). Вычислим объем цилиндроида Т.

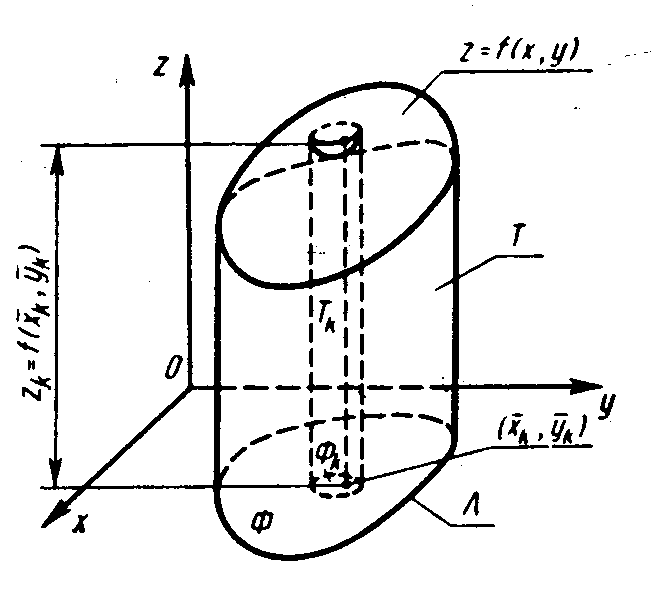Рис. 1.2

Для этого разобьем фигуру с помощью произвольной сетки гладких линий на части Ф_к. Границу каждой такой части примем за направляющую цилиндрической поверхности, образующие которой параллельны оси OZ. Эти поверхности разобьют цилиндроид Т на столбики (элементарные цилиндры), объем каждого из них приближенно выразится произведением f(x, y) S_к (рис. 1.2). Сумма таких произведений равна объему некоторого «ступенчатого» тела, объем которого приближенно равен объему V цилиндроида Т, т.е.

V  S_к. (1.4)

Формула (1.4) позволяет найти объем V с любой степенью точности, если число частичных фигур Ф_к достаточно велико, а диаметр d разбиения {Ф_к } достаточно мал.

Объемом цилиндроида Т называется предел правой части равенства (1.4) (если он существует) при d  0, т.е.

T = S_к = . (1.5)

Итак, при f(x, y) > 0, (x, y)  Ф объем цилиндроида Т вычисляется по формуле (1.5). В этом состоит геометрический смысл двойного интеграла. Перейдем к рассмотрению физического смысла двойного интеграла. Будем называть средней плотностью плоской материальной фигуры Ф отношение ее массы к площади, а плотностью материальной фигуры в данной ее точке – предел средней плотности элементарного участка фигуры, стягивающегося в эту точку. Предположим, что материальная квадрируемая фигура имеет плотность (x, y), которая является непрерывной функцией от (x, y) Ф. При f(x, y)=(x, y) двойной интеграл представляет собой массу материальной фигуры. Действительно, рассмотрим разбиение {Ф_к} фигуры Ф с площадями S₁, S₂, …, S_n и диаметрами d₁, d₂, …, d_n . Наибольший из диаметров обозначим через d. Если d мало, то в пределах геометрической фигуры Ф_к плотность (x, y), будучи непрерывной функцией, суммируется незначительно и приближенно может считаться постоянной величиной. Значение этой постоянной можно принять равным значению  ( ) плотности  (x, y) в некоторой произвольной точке ( ) элементарной частичной фигуры Ф_к. В этом случае масса частичной фигуры Ф_к приближенно равна произведению f ( )S_к, а масса всей фигуры Ф – сумме таких произведений

m ≈ )∆S_k. (1.6)

За точное значение искомой массы m примем предел правой части равенства (1.6) при d  0. Т.к. правая часть равенства (1.6) есть двумерная интегральная сумма для функции  (x, y) по разбиению {Ф_к} с отмеченными точками ( ), то масса материальной фигуры Ф равна двойному интегралу от плотности  (x, y) по области Ф

m  S_к = . (1.7)

В этом состоит физический смысл двойного интеграла.

Приведем признаки существования двойного интеграла.

Теорема 1 (необходимый признак)

Функция f: Ф  R, интегрируемая на Ф  R², ограничена на Ф.

Теорема 2 (первый достаточный признак)

Функция f: Ф  R, непрерывная на компактной фигуре Ф с научно-гладкой границей, интегрируема на Ф.

Теорема 3 (второй достаточный признак)

Функция f: Ф  R, непрерывная на компактной фигуре Ф всюду, за исключением конечных разрывов (скачков) на конечном числе гладких кривых вида y = (x) и x = (y) интегрируема на Ф.

Свойства двойного интеграла

1. Двойной интеграл по области Ф равен площади этой области.

2. Свойство аддитивности

Если функция f интегрируема в области Ф, а область Ф разбита на две связные и не имеющие общих внутренних точек области Ф₁ и Ф₂, то f(x, y) интегрируема в каждой из областей Ф₁ и Ф₂, причем

= + . (1.8)

Эта теорема справедлива для любого числа слагаемых.

3. Свойство линейности

Если функции f₁ и f₂ интегрируемы в области Ф, то функция c₁f₁ + c₂f₂, где c₁ и c₂ – любые вещественные числа, также интегрируема в области Ф, то

[с₁f₂(x,y)+c₂f₂(x,y)]ds=c₁ f₁(x,y)ds+c₂ f₂(x,y)ds. (1.9)

4. Свойство монотонности

Если функции f₁(x, y) и f₂(x, y) интегрируемы в области Ф и всюду в этой области f₁(x, y)  f₂(x, y), то

f₁(x, y) ds  f₂(x, y) ds. (1.10)

В частности, если f(x, y)  0, то f(x, y) ds 0.

5. Теорема об оценке абсолютной величины интеграла

Если функция f(x, y) интегрируема в области Ф, то и функция │f(x, y)│ тоже интегрируема в этой области, причем

│ f(x, y) ds│ ≤ │ f(x, y)│ ds (1.11)

т.е. абсолютная величина двойного интеграла не превосходит двойного интеграла от абсолютной величины подынтегральной функции.

6. Теорема о среднем значении

Если функция f непрерывна в замкнутой ограниченной области Ф, то найдется такая точка ( )  Ф, что

f(x, y)ds = f(x, y) S, (1.12)

где S – площадь области.

Свойство 6 имеет следующую геометрическую интерпретацию: объем V цилиндроида Т, ограниченного снизу связной компактной фигурой Ф, сбоку цилиндрической поверхностью, а сверху – непрерывной поверхностью z = f(x, y), равен объему прямого цилиндра с основанием Ф и высотой f( ), равной значению функции f(x, y) в некоторой точке ( )  Ф (рис. 1.3). Значение функции, определяемое по формуле (1.12), называется средним значением функции f(x, y).

Рис. 1.3