6. Формула интегрирования по частям определенном интеграле

Теорема. Если функции u(x) и v(x) имеют непрерывные производные на отрезке , то справедлива формула

(8.1)

Формула (8.1) называется формулой интегрирования по частям в определенном интеграле.

Пример 1. Вычислить

Р е ш е н и е. Положим , ; отсюда и по формуле (8.1) находим

Пример 2. Вычислить

Р е ш е н и е. Положим отсюда и по формуле (8.1) имеем

Пример 3. Вычислить

Р е ш е н и е. Положим , ; отсюда и по формуле (8.1) находим

9. Некоторые физические и геометрические приложения определенного интеграла

1. Площадь криволинейной трапеции. Пусть на плоскости Oxy дана фигура, ограниченная отрезком оси Ох, прямыми , и графиком непрерывной и неотрицательной функции на . Это криволинейная трапеция, площадь s которой может быть вычислена по формуле

(9.1)

Итак, определенный интеграл от неотрицательной непрерывной функции по численно равен площади криволинейной трапеции с основанием , ограниченной сверху графиком функции . В этом и заключается геометрический смысл определенного интеграла.

Пример 1. Найти площадь фигуры, ограниченной графиком функции прямой и осью Ох.

Р е ш е н и е. По формуле (9.1) имеем

Если , то s  1/2; если то s  1/3, и т. д.

Пусть фигура ограничена снизу и сверху графиками функций и (рис. 3), где две непрерывные функции. Если обе функции неотрицательны, то площадь s данной фигуры равна разности площадей криволинейных трапеций, ограниченных сверху соответственно графиками функций

Рис. 3 Рис. 4

Следовательно,

(9.2)

Заметим, что формула (9.2) справедлива и тогда, когда и не являются неотрицательными.

Пример 2. Вычислить площадь фигуры, ограниченной графиками функций и (рис. 4).

Р е ш е н и е. Найдем абсциссы точек пересечения прямой yx с параболой . Решая систему уравнений получаем Это и есть пределы интегрирования. Искомая площадь фигуры согласно формуле (9.2) такова:

З а м е ч а н и е. Для вычисления площади криволинейной трапеции в случае, когда верхняя граница задана параметрическими уравнениями причем в формуле (9.1) надо сделать замену переменной, положив Тогда получим .

Рис. 5 Рис. 6

Пример 3. Вычислить площадь фигуры, ограниченной эллипсом

Р е ш е н и е. Эллипс симметричен относительно осей координат, поэтому достаточно вычислить площадь части фигуры, находящейся в I четверти (рис. 5). Следовательно, искомая площадь равна

В частности, если , то получаем известную формулу площади круга

2. Площадь криволинейного сектора. Пусть кривая АВ задана в полярных координатах уравнением причем функция непрерывна и неотрицательна на отрезке . Плоскую фигуру, ограниченную кривой АВ и двумя лучами, составляющими с полярной осью углы и будем называть криволинейным сектором (рис. 6). Площадь криволинейного сектора находится по формуле

(9.3)

Пример 4. Вычислить площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда: где а – положительное число (рис. 7).

Р е ш е н и е. При изменении от 0 до полярный радиус описывает кривую, ограничивающую криволинейный сектор ОАВС. Поэтому по формуле (9.3) имеем

Расстояние от точки С до полюса равно . Поэтому круг радиуса ОС имеет площадь т. е. площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна 1/3 площади круга с радиусом, равным наибольшему из полярных радиусов витка. К этому выводу пришел Архимед.

Рис. 7 Рис. 8

3. Длина дуги кривой. Пусть плоская кривая AB задана уравнением y=f(x), где f(x) – непрерывная функция на отрезке . Разобьем кривую АВ на n произвольных частей точками в направлении от А к В. Соединив соседние точки хордами, получим некоторую вписанную в кривую АВ ломаную, длину которой обозначим через Р (рис.8). Через обозначим длину одного звена ломаной, а через длину наибольшего из звеньев:

Определение. Число L называется пределом длин ломаных P при если для любого существует такое, что для всякой ломаной, у которой , выполняется неравенство

Если существует предел L длин P вписанных в кривую ломаных при то этот предел называется длиной дуги АВ.

Если функция непрерывна вместе с на отрезке , то длина дуги АВ выражается формулой

(9.4)

Рис. 9 Рис. 10

Пример 5. Вычислить длину дуги верхней ветви полукубической параболы если (рис. 9).

Р е ш е н и е. Из уравнения находим: Следовательно, по формуле (9.4) получим

З а м е ч а н и е 1. Для вычисления длины дуги в случае, когда кривая AB задана параметрически уравнениями , где и значения параметра t, соответствующие значениям x=a, x=b, т.е. в формуле надо сделать замену переменной, положив Тогда получим

(9.5)

Пример 6. Вычислить длину дуги одной арки циклоиды: (рис. 10).

Р е ш е н и е. Из уравнений циклоиды находим: Когда х пробегает отрезок параметр t пробегает отрезок Следовательно, искомая длина дуги равна

З а м е ч а н и е 2. Для вычисления длины дуги в случае, когда кривая AB задана в полярных координатах уравнением где имеет непрерывную производную на отрезке , и точкам A и B соответствуют значения , равные и , нужно перейти от полярных координат к прямоугольным. Тогда получим параметрическое задание кривой AB уравнениями . Так как то формула (9.5) принимает вид

(9.6)

Пример 7. Вычислить длину первого витка спирали Архимеда: (см. рис. 7).

Р е ш е н и е. Первый виток спирали образуется при изменении полярного угла от 0 до . Поэтому по формуле (9.6) искомая длина дуги равна

4. Объем тела вращения. Пусть функция непрерывна и неотрицательна на отрезке . Тогда тело, которое образуется вращением вокруг оси Ох криволинейной трапеции, ограниченной сверху графиком функции , имеет объем

(9.7)

Пример 8. Вычислить объем тора. Тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга . Форму тора имеет, например, баранка.

Р е ш е н и е. Пусть круг вращается оси Ох (рис. 12). Объем тора можно представить как разность объемов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ох.

Рис. 11 Рис. 12

Уравнение окружности LBCD имеет вид причем уравнение кривой BCD а уравнение кривой BLD

Используя формулу (9.7), получаем для объема тора выражение

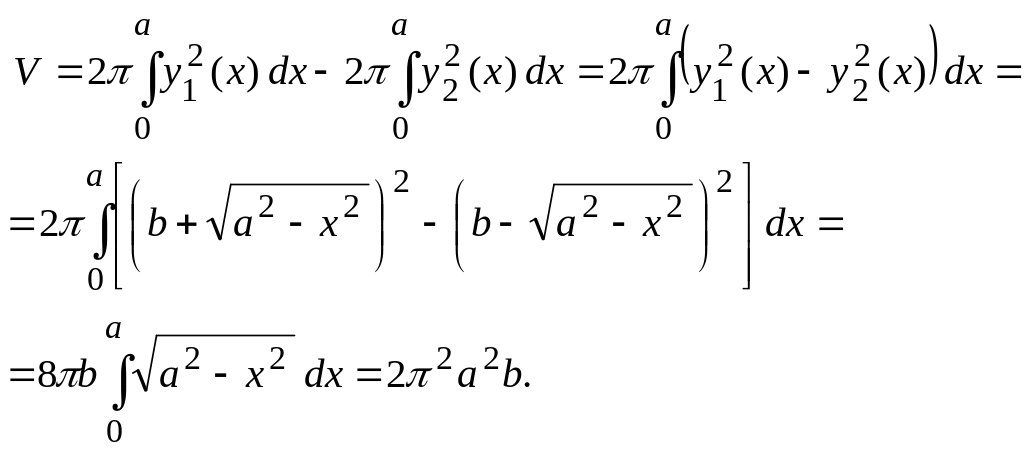
5. Площадь поверхности вращения. Пусть функция неотрицательна и непрерывна вместе со своей первой производной на отрезке . Тогда поверхность, образованная вращением графика этой функции вокруг оси Ох, имеет площадь Р, которая может быть вычислена по формуле

(9.8)

З а м е ч а н и е. Если поверхность получается вращением вокруг оси Ох кривой АВ, заданной параметрическими уравнениями причем изменяется от a до b при изменении t от до то производя в интеграле (9.8) замену переменной получаем

(9.9)

Наконец, если кривая задана уравнением в полярных координатах: где имеет непрерывную производную на , то этот случай, как уже отмечалось в п. 3, сводится к параметрическому заданию кривой и формула (9.9) принимает вид

Пример 9. Вычислить площадь P поверхности шарового пояса, образованного вращением полуокружности вокруг оси Ох.

Р е ш е н и е. По формуле (9.8) получаем

где h – высота пояса.

Пример 10. Вычислить площадь поверхности, полученной вращением одной арки циклоиды вокруг оси Ох.

Р е ш е н и е. По формуле (9.9) имеем

6. Работа переменной силы. Из рассмотренных выше задач, связанных с геометрическим приложением определенного интеграла, следует, что для их решения применяется один и тот же вычислительный метод: приближенное значение искомой величины представляется в виде интегральной суммы, а затем предельным переходом получается точное значение в виде интеграла. С помощью этого же метода решается целый ряд других задач механики, физики и техники. В качестве примера вычислим работу переменной силы.

П усть материальная точка перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину, зависящую от х. Требуется определить работу A, совершаемую силой F по перемещению материальной точки вдоль оси Ох из точки в точку . Функция предполагается непрерывной на отрезке (рис. 13).

Рис. 13 Рис. 14

Разобьем произвольно отрезок на n частей точками Выберем на каждом частичном отрезке точку . Сила, действующая на материальную точку на отрезке , изменяется от точки к точке. Но если длина отрезка мала, то значение силы в точках отрезка мало отличается от ее значения в любой точке , так как непрерывна. Поэтому работу , совершаемую силой F на можно считать приближенно равной работе, совершаемой на том же отрезке постоянной силой , т. е.

Проводя аналогичные рассуждения для каждого отрезка разбиения, получаем приближенное значение работы A силы F на всем отрезке:

С другой стороны, сумма в правой части равенства является интегральной суммой для функции F(x). Так как функция непрерывна на то предел этой суммы при существует и равен определенному интегралу от функции по отрезку Таким образом,

(9.10)

Пример 11. Определить работу A, необходимую для запуска тела массой m с поверхности Земли вертикально вверх на высоту h (рис. 14).

Р е ш е н и е. Обозначим через F силу притяжения тела Землей. Пусть масса Земли. Согласно закону Ньютона где х - расстояние от тела до центра Земли. Полагая получаем где R – радиус Земли. При сила F(R) равна весу тела P=mg, т.е. откуда и Таким образом, по формуле (9.10) получаем