Формула ньютона – лейбница
Вычисление
определенных интегралов методом,
основанным на определении интеграла
как предела интегральной суммы, как
правило, связано с большими трудностями.
Существует более удобный метод вычисления
определенных интегралов, который, как
будет показано, основан на установленной
ранее связи между неопределенным и
определенным интегралами. Было
установлено, что функция
- непрерывная
на отрезке
,
имеет на этом отрезке первообразные,
причем одной из них является функция
Пусть
F(x)
– любая другая первообразная для функции
f(x)
на том же
отрезке
Так как первообразные Ф(х)
и F(x)
отличаются на постоянную, то имеет место
равенство
где С
– некоторое число. Подставляя в это
равенство значение
,
имеем
т. е. для любого
Полагая
,
получаем основную формулу интегрального
исчисления
(6.1)
которая называется формулой Ньютона-Лейбница. Разность
принято
условно записывать:
и поэтому
формула
(6.1) принимает вид
Подчеркнем,
что в формуле (6.1) в качестве
можно взять любую первообразную для
на отрезке
.
Формула (6.1) дает простой метод вычисления определенного интеграла: определенный интеграл от непрерывной функции равен разности значений любой ее первообразной, вычисленных для верхнего и нижнего пределов интегрирования. Эта формула открывает широкие возможности для вычисления определенных интегралов, поскольку задача вычисления определенного интеграла сводится к задаче вычисления неопределенного интеграла, которая достаточно полно изучена. Рассмотрим п р и м е р ы.
1.
2.
3.
4.
З а м е ч а н и е. Формула Ньютона-Лейбница была выведена в предположении, что подынтегральная функция непрерывна. При некоторых условиях формула Ньютона-Лейбница имеет место и для разрывных функций.
Замена переменной в определенном интеграле
Теорема.
Пусть
– непрерывная функция на отрезке
.
Тогда, если: 1)
функция
дифференцируема на
и
непрерывна на
;
2)
множеством значений функции
является отрезок
;
3)
и
, то справедлива формула
(7.1)
Формула (7.1) называется формулой замены переменной или подстановки в определенном интеграле.
Пример 1. Вычислить
Р
е ш е н и е. Рассмотрим подстановку
,
Проверим законность такой подстановки.
Во-первых, функция
непрерывна
на
во-вторых, функция
дифференцируема
на
и
непрерывна на
и, в третьих, при изменении t
от 0 до
функция
изменяется от 0 до 1, причем х(0)=0
и
.
Таким образом, данная подстановка
удовлетворяет всем условиям теоремы.
Применяя формулу (7.1), получаем
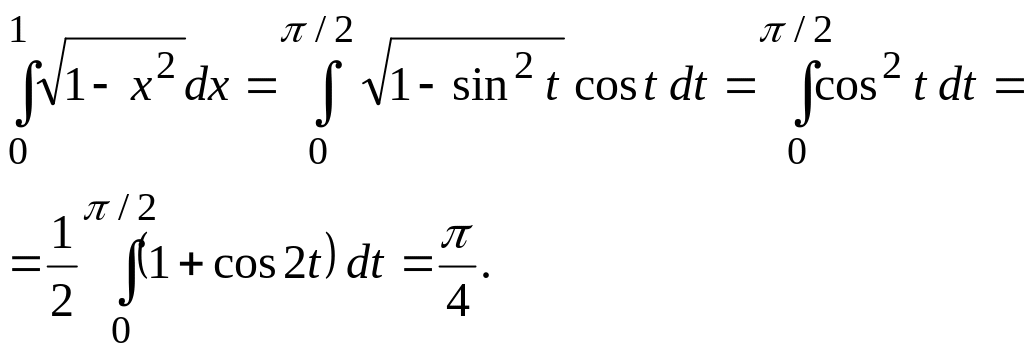
З а м е ч а н и е 2. При использовании формулы (7.1) необходимо проверять выполнение перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен и неверный результат.
Пример
2. Вычислить
Р
е ш е н и е. Имеем
С другой стороны,
Подстановка
формально приводит к следующему
результату:
Получен
неверный результат, так как
.
Это произошло потому, что функция
разрывна при
и не удовлетворяет условиям теоремы.