ФГБОУ ВПО “Воронежский

государственный технический университет”

Кафедра прикладной математики и механики

Методические указания

по математике к разделу

«Определенный интеграл и его приложение»

для студентов направления подготовки бакалавров 21.03.01 «Нефтегазовое дело» (профиль «Эксплуатация

и обслуживание объектов транспорта и хранения

нефти, газа и продуктов переработки»)

очной формы обучения

Воронеж 2015

Составители:	канд. физ.-мат. наук канд. физ.-мат. наук	А.П. Бырдин, М. И. Зайцева,
	канд. техн. наук	А.А. Сидоренко

УДК 517.2 (07)

Методические указания по математике к разделу «Определенный интеграл и его приложение» для студентов направления подготовки бакалавров 21.03.01 «Нефтегазовое дело» (профиль «Эксплуатация и обслуживание объектов транспорта и хранения нефти, газа и продуктов переработки»)

очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост.: А.П. Бырдин, М.И. Зайцева, А.А Сидоренко. Воронеж, 2015. 48 с.

Методические указания предназначены для самостоятельного изучения темы «Определенный интеграл и его приложение». Изложен теоретический материал и типовые примеры, предложены задачи для самостоятельной работы. Методические указания рассчитаны на студентов первого курса указанного направления, но могут быть использованы и для других направлений.

Методические указания подготовлены в электронном виде в текстовом редакторе Word 2003 и содержатся в файле НГД-Определенный интеграл.doc.

Ил. 15. Библиогр.: 5 назв.

Рецензент канд. физ.-мат. наук, доц. Е.И. Иохвидов

Ответственный за выпуск зав. кафедрой д-р техн.

наук, проф. В.И. Ряжских

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

• ФГБОУ ВПО “Воронежский государственный технический университет”, 2015

Определенный интеграл

1. Определение определенного интеграла

Пусть функция определена на отрезке Разобьем этот отрезок на n произвольных частей точками:

Обозначим это разбиение через а точки будем называть точками разбиения. В каждом из полученных частичных отрезков выберем произвольную точку Через обозначим разность которую условимся называть длиной частичного отрезка Образуем сумму:

(1.1)

которую назовем интегральной суммой для функции f(x) на соответствующей данному разбиению на частичные отрезки и данному выбору промежуточных точек Геометрический смысл суммы очевиден: это сумма площадей прямоугольников с основаниями и высотами если (рис.1). Обозначим через длину наибольшего частичного отрезка разбиения : .

Определение. Если существует конечный предел I интегральной суммы (1.1) при , то этот предел называется определенным интегралом от функции по отрезку и обозначается следующим образом:

или (1.2)

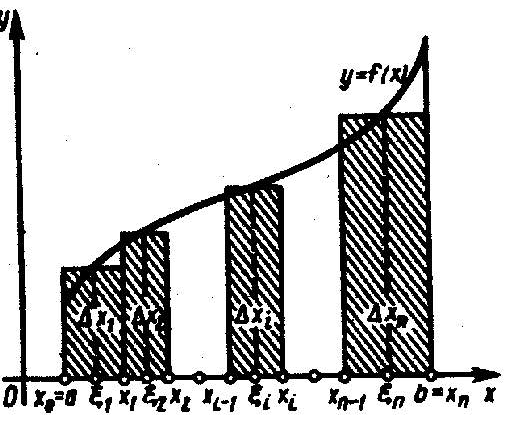
Рис. 1

В этом случае, функция называется интегрируемой на отрезке . Числа a и b называются соответственно нижним и верхним пределами интегрирования, - подынтегральной функцией, х – переменной интегрирования.

Из определения определенного интеграла следует, что величина интеграла (1.2) зависит только от вида функций и от чисел a и b. Следовательно, если заданы и пределы интегрирования, то интеграл (1.2) определяется однозначно и представляет собой некоторое число. Отсюда, в частности, следует, что определенный интеграл не зависит от выбора обозначения для аргумента подынтегральной функции, т. е. от обозначения переменной интегрирования: и т. д.

Теорема (необходимое условие интегрируемости функции). Если функция интегрируема на отрезке то она ограничена на этом отрезке.