4.2. Управление общим риском системы

В силу гладкости функции плотности распределения вероятностей, по предельно допустимому значению коэффициента загрузки центрального процессора каждого сервера при и по максимальному числу открытых соединений, поведение функции риска всей системы, время отказов компонентов которой задается функцией плотности вероятностей Вейбулла, будет зависеть от ее поведения около точек локальных экстремумов. В рассматриваемом примере система состояла из четырех компонент, причем параметры функций риска этих компонент были заданы таким образом, что общая функция риска колебалась в заданной полосе неравномерности . Значения этих параметров возьмем в качестве базовых.

Для того чтобы создать движение общей функции риска, достаточно задать планируемые изменения риска системы в окрестностях точек экстремумов. В случае четырех компонент функция риска будет содержать восемь параметров: и , , а локальных экстремумов будет семь: четыре максимума и три минимума. В связи с этим для нахождения приращений, обеспечивающих заданное движение функции риска, будем составлять две системы линейных уравнений с постоянными коэффициентами относительно искомых приращений. Коэффициентами этой системы будут значения функций чувствительности , , найденные в точках t, при которых общая функция риска имеет экстремумы. Первую систему составим относительно искомых приращений , , , , , , :

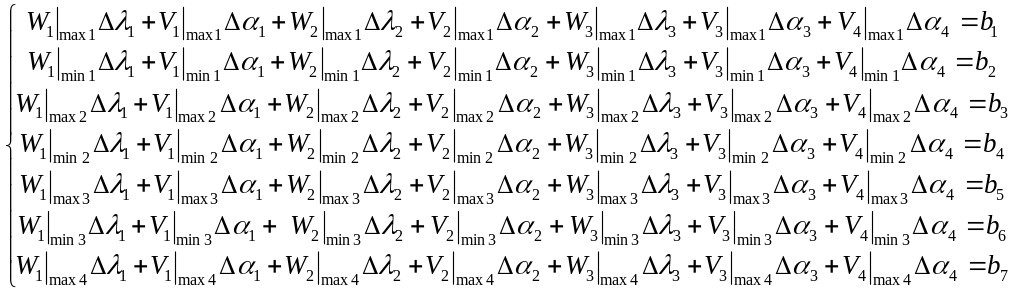
где каждое уравнение системы представляет собой первое приближение дополнительного движения риска системы в точках экстремумов:

–

первое приближение дополнительного движения риска системы в первой точке локального максимума;

–

первое приближение дополнительного движения риска системы в первой точке локального минимума;

–

первое приближение дополнительного движения риска системы во второй точке локального максимума и т.д.

– задаваемые значения первого приближения дополнительного движения риска системы в точках экстремумов риска системы (требуемое изменения риска системы в точках экстремумов), количество которых будет равно , ; – количество компонентов мультисерверной системы (4.7);

– задаваемое значение первого приближения дополнительного движения риска системы в точке первого максимума; – задаваемое значение первого приближения дополнительного движения риска системы в точке первого минимума; – задаваемое значение первого приближения дополнительного движения риска системы в точке второго максимума и т.д.

Задавая значения первого приближения дополнительного движения риска системы в точках экстремумов, будем находить вариации базовых параметров предельно допустимого значения числа открытых соединений и коэффициентов загрузки центральных процессоров, входящих в критерии определения сервера, на который будет отправлен запрос, обеспечивающих такое дополнительное движение, чтобы экстремумы общего риска системы после данного движения были равны максимальным значениям общего риска до выполнения движения плюс заданные значения (задаваемые могут быть как положительными, так и отрицательными; максимальные значения можно уменьшать в точках локальных максимумов функции риска системы, минимальные значения увеличивать в точках локальных экстремумов, тем самым уменьшая как величину глобального максимального значения общего риска системы, а, следовательно, уменьшая диапазон неравномерности ).

Решаем систему (4.7), например, матричным методом, записав ее в следующем виде:

,

где – матрица системы:

;

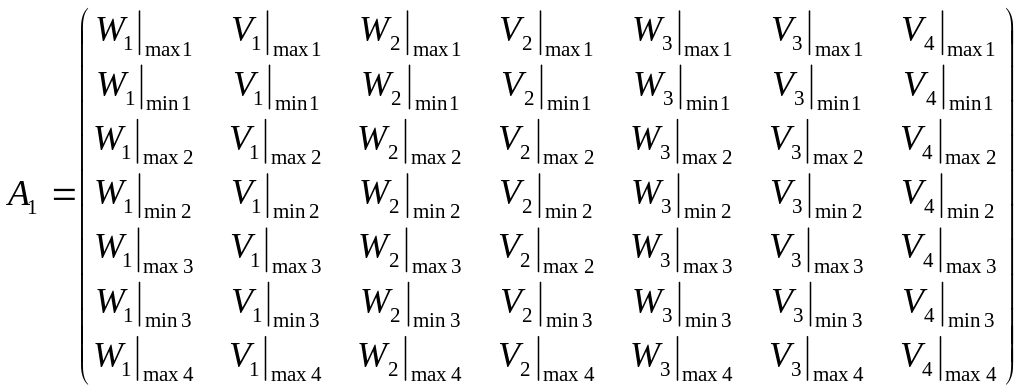– вектор-столбец свободных членов (заданные вариации общей функции риска в точках, где она достигает своих экстремумов;

– вектор-столбец неизвестных приращений, обеспечивающих заданное движение:

.

Если определитель системы (4.7) отличен от нуля, то система имеет единственное решение:

, , , ,

, , .

Вторую систему составим относительно искомых приращений , , , , , , :

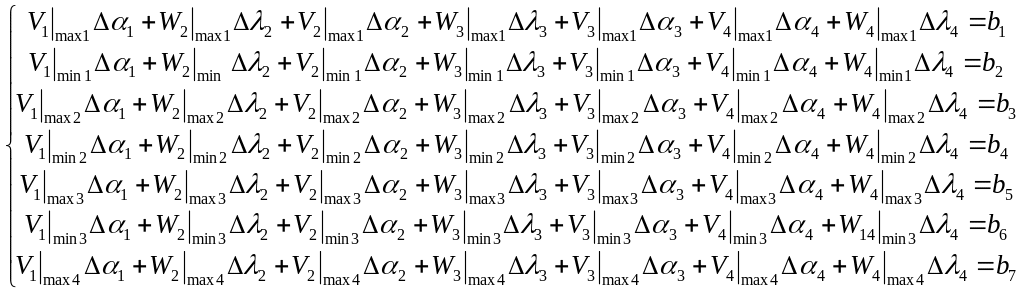. (4.8)

Тогда в качестве приращений, обеспечивающих заданное движение риска, будем выбирать следующие значения:

, , , , , , . (4.9)

Если мы хотим сузить диапазон неравномерности , то в точках, где общий риск системы при базовых значениях параметров достигает локальных максимумов, выбираем значения , а для локальных минимумов берем . Будем сужать диапазон неравномерности . Рассмотрим, в качестве примера, вариации общего риска, приведенные на рис. 4.2.

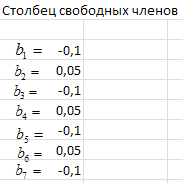
Рис. 4.2. Вариации общего риска

Будем искать, при каких вариациях , , , , , , , базовых параметров и , , будет получено заданное движение общего риска системы при (в точке первого максимума), (в точке первого минимума), (в точке второго максимума), (в точке второго минимума), (в точке третьего максимума), (в точке третьего минимума), (в точке четвертого максимума).

Элементами матрицы системы (4.7) являются значения функций чувствительности общего риска системы, вычисленные в точках, при которых этот риск имеет экстремумы.

Тогда решением системы (4.7) будут следующие вариации базовых параметров (рис. 4.3. а).

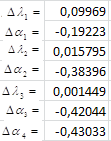
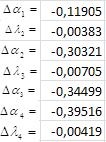
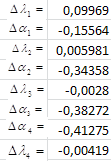
а) б) в)

Рис. 4.3. Найденные вариации базовых параметров:

а) решение системы (4.7); б) решение системы (4.9);

в) найденные средние значения для вариаций базовых параметров

Решением системы (4.8) будут значения вариаций базовых параметров, приведенных на рисунке 4.3 б). Найденные средние значения для вариаций базовых параметров показаны на рисунке 4.3 в).

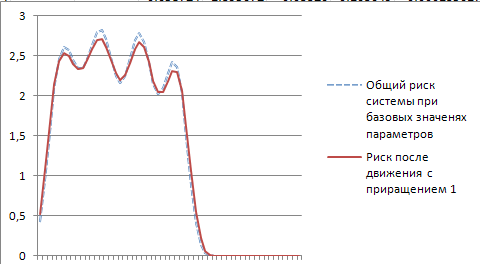
Рис. 4.4. Графики функций общего риска системы, полученного при базовых значениях параметров, и после движения

Графики функции общего риска системы при базовых значениях параметров и общей функции риска, полученной в результате движения созданного заданными вариациями общей функции риска (рис. 4.2) и полученными в результате вариаций параметров (рис. 4.3 в)), приведены на рис. 4.5.

Как иллюстрирует рис. 4.5, пиковые значения общего риска после движения уменьшились, а в точках минимума – значение общей функции риска увеличилось.

Движение общего риска системы при заданных вариациях общего риска в точках экстремумов: , , , , , , и при полученных вариациях базовых параметров: , , , , , , , приведено на рис. 4.6.

Рис. 4.5. Графики функций общего риска системы, полученного при базовых значениях параметров, и после движения

.

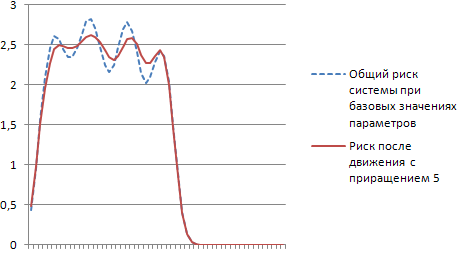
Рис. 4.6. Движение общего риска системы при заданных вариациях общего риска в точках экстремумов

Результаты расчетов для получения движения общего риска приведены в таблице.

Результаты расчетов

№	Задаваемые значения первого приближения дополнительного движения риска системы в токах экстремумов
1
	-0.01	0.08	-0.1	0.08	-0.05	0.08	-0.05
	Полученные приращения базовых параметров общего риска системы
	-0.029379	-0.116647	-0.000167	-0.326451	-0.002794	-0.486225	-0.23	0.0011
Продолжение таблицы
2	Задаваемые значения первого приближения дополнительного движения риска системы в токах экстремумов
	b1	b2	b3	b4	b5	b6	b7
	-0.2	0.1	-0.2	0.1	-0.2	0.15	-0.2
	Полученные приращения базовых параметров общего риска системы
	0/150569	-0.29362	-0.006932	-0/67153	-0/00814	-0.78857	-0.84	-0.0063
№	Задаваемые значения первого приближения дополнительного движения риска системы в токах экстремумов
3	Задаваемые значения первого приближения дополнительного движения риска системы в токах экстремумов
	b1	b2	b3	b4	b5	b6	b7
	-0.3	0.1	-0.3	0/1	-0/1	0.1	-0.1
	Полученные приращения базовых параметров общего риска системы
	0.248567	-0.42807	0/07393	-0.849854	-0.013004	-0.74297	-0.39	-0.0104
4	Задаваемые значения первого приближения дополнительного движения риска системы в токах экстремумов
Окончание таблицы
	b1	b2	b3	b4	b5	b6	b7
	-0.15	0.1	-0.25	0.2	-0.1	0.15	-0.01
	Полученные приращения базовых параметров общего риска системы
	-0.026511	-0.191005	-0.007764	-0.677834	-0.005628	-0.820019	-0.07	0.001

Определим ограничения, накладываемые на значения уравнения движения в точках экстремумов. Находим отклонения от верхней границы полосы неравномерности значения общей функции риска в точках локальных максимумов:

( ).

Аналогично находим отклонения от нижней границы полосы неравномерности ( ) значения общей функции риска в точках локальных минимумов:

, .

Движение в точках максимумов общего риска должно удовлетворять неравенству

,

т.е., после выполнения движения общая функция риска не должна опуститься ниже середины полосы неравномерности; аналогично, движение в точках минимумов общего риска должно удовлетворять неравенству

.

Если хотим уменьшить риск после движения, то берем величину со знаком минус, а – со знаком плюс.

Так как изменения параметров , общей функции риска должны быть небольшими (точки , должны находиться в окрестности базовых параметров), то и значение уравнения движения в рассматриваемых экстремальных точках должно быть небольшим. Если хотим значительно уменьшить значение функции риска, а также полосы неравномерности, то нужно применить итерационный процесс изменения: найденные скорректированные значения параметров функции риска принимаем за базисные, и повторяем вычисления.

Таким образом, через предельно допустимые значения числа открытых соединений и предельно допустимые значения коэффициентов загрузки центральных процессоров компонентов МСС получены аналитические выражения для управления общим риском систем на основе заданного движения в точках экстремумов. Кроме того, получены аналитические выражения для проведения ранжирования вкладов вариаций рисков отдельных компонент в вариацию общего риска. Это позволяет определить относительный вес каждой вариации риска компоненты, что дает возможность выдать рекомендации по определению рациональных направлений совершенствования системы защиты с целью уменьшения рисков.

Получено, что влияние рисков отдельных компонентов МСС на риск всей системы может быть определено методами теории чувствительности.

На основе анализа структурной специфики МСС и динамики информационных процессов, использовались положения теории чувствительности для оценки защищенности.