3. Аналитическая оценка рисков атакуемых мультисерверных систем

3.1. Оценка параметров риска для компонентов мультисерверных систем

Рассмотрим задачу получения аналитических выражений для анализа, оценки и управления рисками с использованием параметров функций рисков отдельных компонентов, позволяющих настроить параметры защиты системы таким образом, чтобы суммарный риск системы находился в заданной полосе неравномерности при реализации угрозы DDoS-атаки.

Ранее было установлено, что плотность вероятности отказов серверов мультисерверной системы можно определить функцией плотности распределения вероятностей Вейбулла:

, , (3.1)

где: – количество серверов, включенных в мультсерверную систему; , , соответственно, максимально допустимое количество открытых соединений на -м сервере и максимально допустимый коэффициент загрузки центрального процессора (ЦП).

Риск отказа сервера без учета шага дискретизации определяется следующей формулой:

,

где – нормированный ущерб.

Следовательно, функция риска для -го сервера примет вид:

, ( ). (3.2)

Найдем значение аргумента , при котором достигаются максимумы рисков ущербов от отказов отдельных серверов. Для этого найдем производную от риска и приравняем ее к нулю:

.

Следовательно, проведя преобразования, получим уравнение:

.

Откуда следует:

. (3.3)

Тогда максимальное значение риска выражается через параметры функции плотности вероятности следующим образом:

Таким образом, имеем

. (3.4)

Зададим значение порогового риска и коэффициент , определяющие требуемый диапазон неравномерности для риска всей системы защиты. Зависимость диапазона неравномерности риска системы и величины диапазона ущерба Д показана на рис. 3.1.

Величина диапазона риска системы определяется соотношением [59]:

.

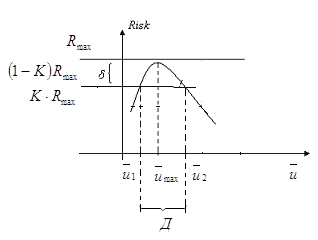
Рис. 3.1. Зависимость диапазона риска и величины нормированного ущерба

Найдем теперь диапазон ущербов в случае, когда система включает серверов ( ).

Тогда диапазон ущербов можно рассматривать как разность между значениями , где – левый корень уравнения , а – правый корень уравнения

.

Таким образом, управляя значениями максимально допустимого количества открытых соединений на -м сервере ( ) и максимально допустимым значением коэффициента загрузки центрального процессора ( ), участвующие в критериях выбора сервера, на который будет отправлен запрос, можно регулировать диапазон ущерба Д и неравномерность .

3.2. Оценка и регулирование рисков мультисерверных систем

Для регулирования общего риска МСС с заданной неравномерностью важным параметрами являются значения локальных экстремумов этой функции, так как при задании требуемого вида общего риска системы количество максимумов должно быть равно количеству компонентов, включенных в систему. В дальнейшем, при управлении общим риском ММС, возникающем при реализации DDoS-атак на ее компоненты, можно будет использовать метод уравнивания в точках экстремумов значений искомой общей функции риска со значениями заданной функции риска в тех же точках. Важно, что полученные оценки параметров позволят заранее оценивать ущербы от нахождения системы в режиме отказа в обслуживании

Рассмотрим случай асинхронных атак на серверы МСС. Поставим теперь задачу нахождения параметров рисков компонентов МСС таким образом, чтобы функция общего риска системы находилась в заданной полосе неравномерности и, тем самым, найдем соответствующие предельные значения для количества открытых соединений на -м сервера сервере и максимально допустимый коэффициент загрузки центрального процессора. В дальнейшем эти значения могут быть использованы сетевым администратором для формирования критериев загрузки серверов МСС для балансировщика нагрузки.

При асинхронных атаках будем реализовывать уравнивание максимальных значений функций рисков для каждого сервера [36].

Получим аналитические выражения для оценки параметров риска всей системы при условии уравнивания пиковых значений функций риска отдельных компонент. Чтобы уравнять пиковые значения рисков для серверов мультисерверной системы, необходимо потребовать выполнения равенства:

,

то есть выполнения условия:

.

Откуда, с учетом значения в случае распределения Вейбулла, получим соотношения, связывающие его параметры:

, . (3.5)

Таким образом, получаем, что администратору необходимо, управляя безопасностью системы, выбрать в качестве одного из критериев безопасности следующее: произведение максимально допустимого количества открытых соединений на -м сервера сервере на максимально допустимый коэффициент загрузки центрального процессора для всех серверов (реальных и виртуальных) должно быть одинаковым. Следовательно, задав максимально допустимое количество открытых соединений для первого сервера и максимально допустимый коэффициент загрузки центрального процессора, можно получить условия выбора таких параметров для остальных серверов, если уравниваем пиковые значения функций риска всех серверов.

Если выразить все параметры , через и , то последнее выражение примет вид:

, . (3.6)

В дальнейшем, используя условия равенства пиковых значений функций риска для каждого сервера, выразим усредненные значения ущербов , через усредненный ущерб первого сервера .

а) Рассмотрим частный случай, когда в МСС включены два сервера ( ). Функция суммарного риска при задается следующим образом:

.

Найдем экстремумы суммарного риска, взяв производную по и приравняв ее к нулю. В результате получим следующее уравнение [23-24, 36]:

После преобразования последнее выражение примет вид:

.

Чтобы получить решение последнего уравнения, приведем это уравнение к одной переменной . Для этого заменим в последнем равенстве на выражение , найденное из условия равенства пиковых значений функций риска (2.6). Откуда получим следующее уравнение [107]:

.

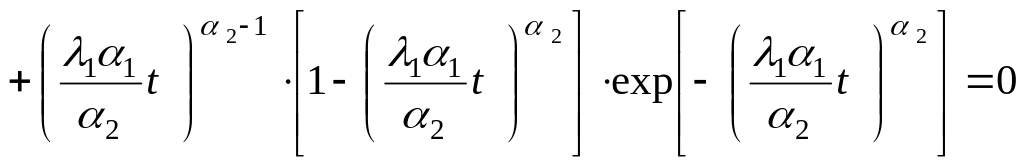Перейдем в последнем уравнении к усредненному ущербу для первого сервера, сделав замену: .

Тогда уравнение для нахождения экстремумов суммарного риска при примет вид:

.

Введем обозначение: .

В результате получим нелинейное уравнение для нахождения экстремумов суммарного риска в случае двух серверов относительно усредненного ущерба :

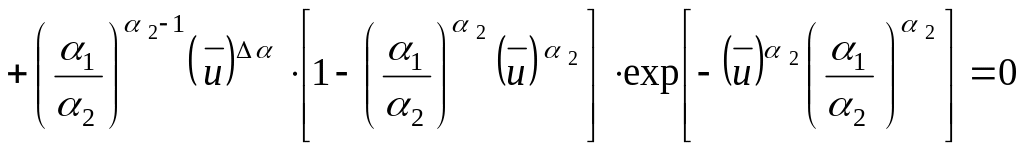. (3.7)

Так как уравниваются максимальные значения функций плотности вероятности, то из полученного соотношения (3.5) следует: если , то и , т.е. функции плотности распределения вероятностей совпадают. Для функции плотности распределения вероятностей Вейбулла параметр формы , поэтому рассматриваем и . В дальнейшем рассматриваем функции плотности распределения вероятностей при условии, что . Если функции плотности распределения вероятностей совпадают, то суммарный риск будет априори велик. Максимальное значение функция плотности распределения вероятностей Вейбулла достигает при .

б) Если в МСС включено серверов , то сумму рисков -го и -го серверов можно записать в следующем виде:

.

В этом случае производная для суммы рисков -го и -го серверов примет вид:

. (3.8)

Воспользовавшись условием равенства пиковых значений функций риска (3.6), получим:

и .

Тогда уравнения (3.8) для нахождения экстремумов функций суммарного риска -го и -го серверов будет выглядеть следующим образом:

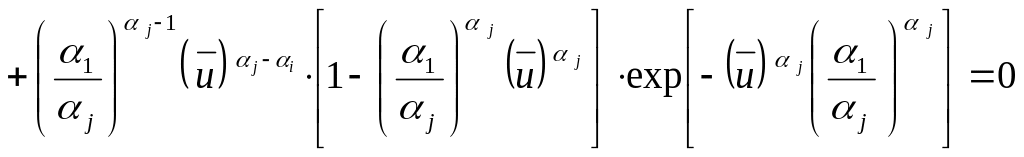. (3.9)

Переход к одной переменной усредненного риска .

Чтобы найти решения уравнений (3.9) и получить графики функций рисков всех серверов в одной системе координат, необходимо перейти к одной переменной.

Перейдем к одной переменной усредненного риска первого сервера , и найдем на оси ущербов значения , , при которых функция риска -го сервера достигает своего максимума.

Определим положения пиковых значений рисков -го сервера на одной оси усредненного ущерба .

Найдем производную от функции по и приравняем ее к нулю. В результате получим уравнение:

.

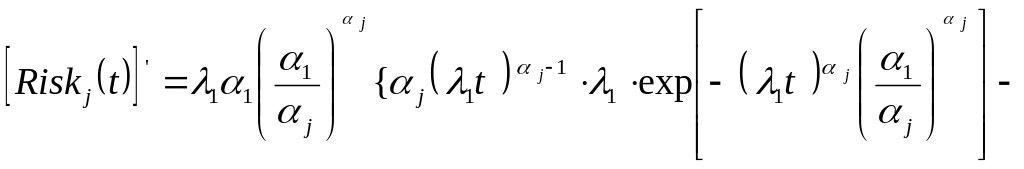
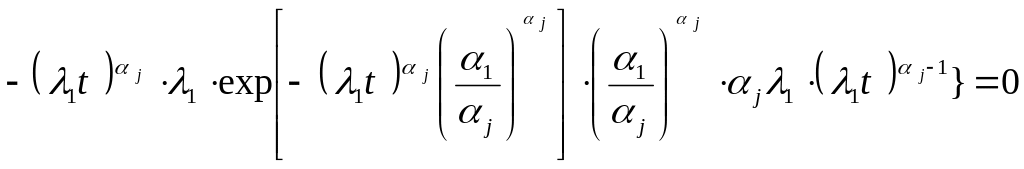После преобразований последнее уравнение примет вид:

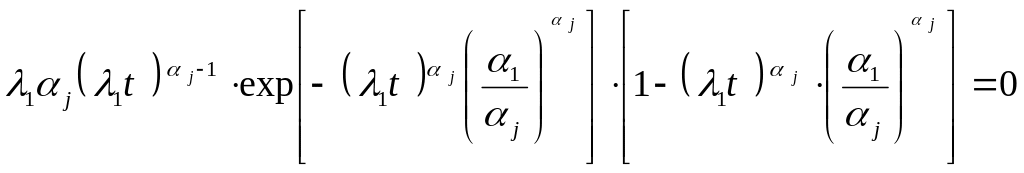(3.10)

Откуда получаем уравнения для нахождения усредненных ущербов на оси , при которых функции риска

,

будут принимать максимальные значения:

. (3.11)

Из последнего уравнения (3.11) видно, что производная равна нулю, если выполняется равенство:

,

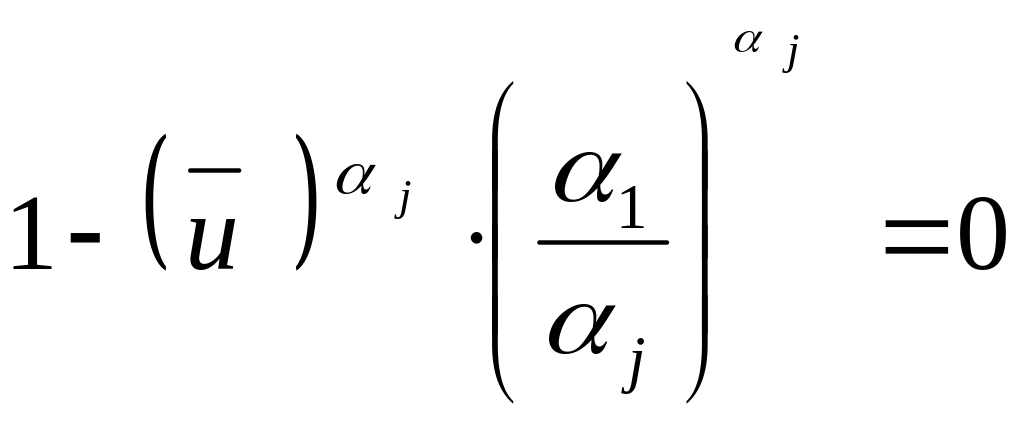из которого находим значение ущерба , при котором риск от отказа -го сервера принимает максимальное значение:

. (3.12)

Функция риска первого сервера принимает максимальное значение при , так как .

Вид функций риска на оси усредненного ущерба показан на рис. 3.2.

Рис. 3.2. Расположение функций риска на оси ущербов

Экстремумов у функции суммарного риска, например, в случае наличия четырех серверов в МСС будет семь: четыре максимума и три минимума. В случае включения серверов экстремумов будет , из них максимумов и минимумов.

Нахождение координат экстремумов суммарного риска.

Максимальные значения суммарного риска не будут совпадать с максимами рисков отдельных компонент. Найдем теперь максимумы функции суммарного риска.

а) Рассмотрим сначала частный случай, когда в МСС включено два сервера ( ). Найдем координаты первого максимума функции суммарного риска. Максимум первой функции риска будет смещаться вправо (рис. 3.3), поэтому будем искать решения уравнения (3.7) в виде:

.

В этом решении – поправка, вносимая в первое решение вторым сервером. Подставим это решение в уравнение (3.7). В результате получим нелинейное уравнение для нахождения поправки :

.

Найдем координаты второго максимума суммарной функции риска. Так как второй максимум при воздействии первого сервера смещается влево, то решение уравнения будем искать в виде:

,

где – поправка, вносимая во второе решение первым сервером.

В результате при нахождении поправки уравнение (3.7) примет вид:

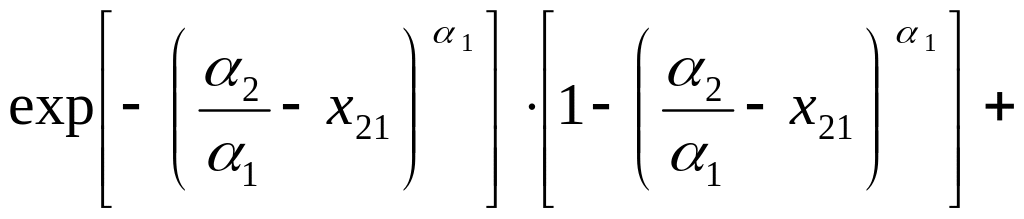
При воздействии первого сервера второй максимум смещается вправо, то решение уравнения (3.9) будем искать в виде

.

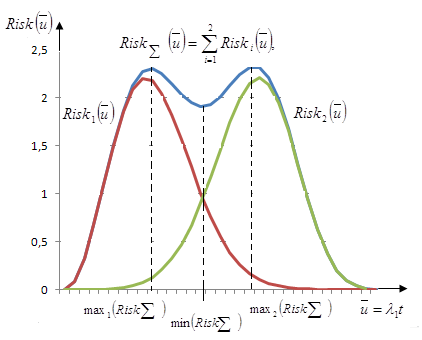
Рис. 3.3. Оценка и регулирование риска системы с двумя серверами

б) Пусть теперь в МСС серверов .

Найдем координаты первого максимума функции суммарного риска. Максимум первой функции риска будет смещаться вправо при всех значениях , поэтому будем искать решения уравнения (3.9) в виде

,

где – поправка, вносимая в первое решение -м сервером ( ).

Тогда уравнение (3.9) будет иметь вид:

.

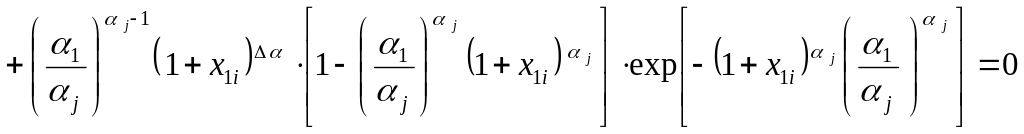В общем случае, так как второй максимум при воздействии -го сервера смещается влево, то решение уравнения (3.9) будем искать в виде:

,

где – поправка, вносимая во второе решение -м сервером ( ).

При нахождения поправки уравнение (3.9) примет вид:

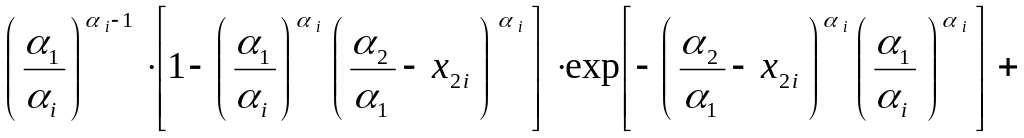
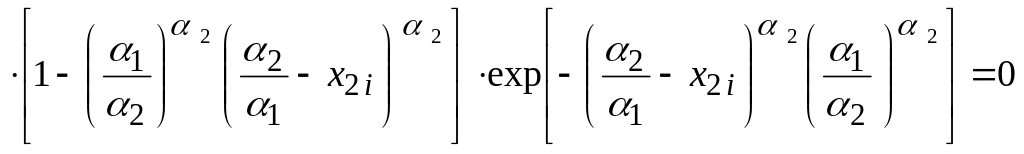
при .

Тогда для нахождения, например, поправки ( , ), вносимой во второе решение третьим сервером, уравнение (3.9) примет вид:

.

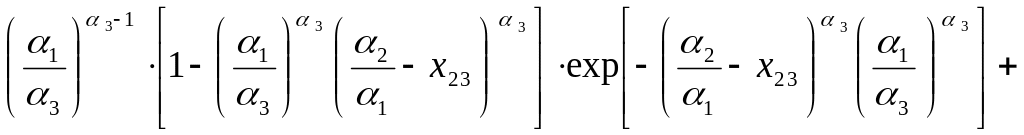
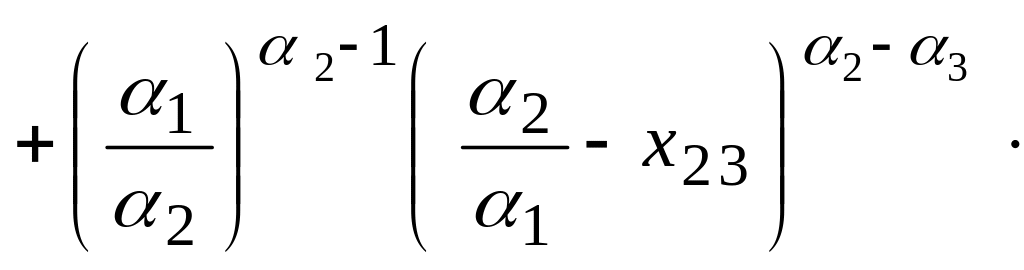
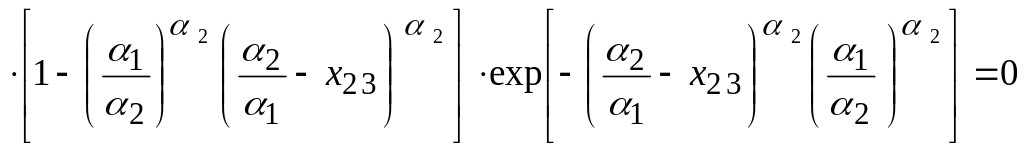В общем случае, используя уравнение, для нахождения поправки вносимой в -е решение -м сервером, получим нелинейное уравнение [23,36]:

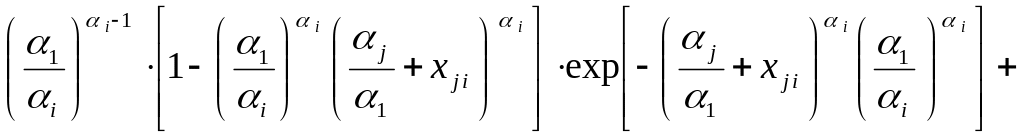
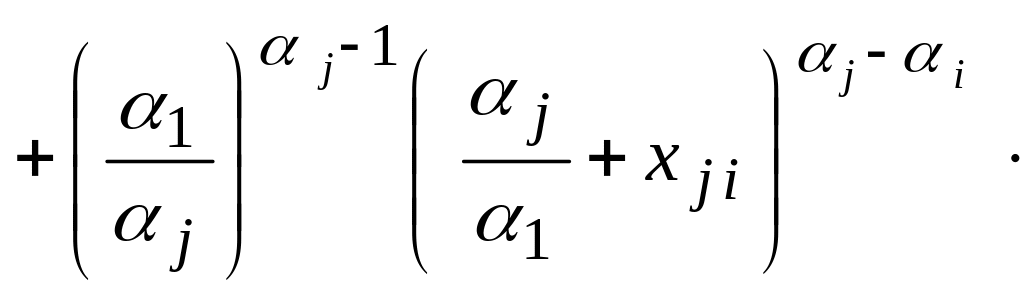
(3.13)

при , и уравнение:

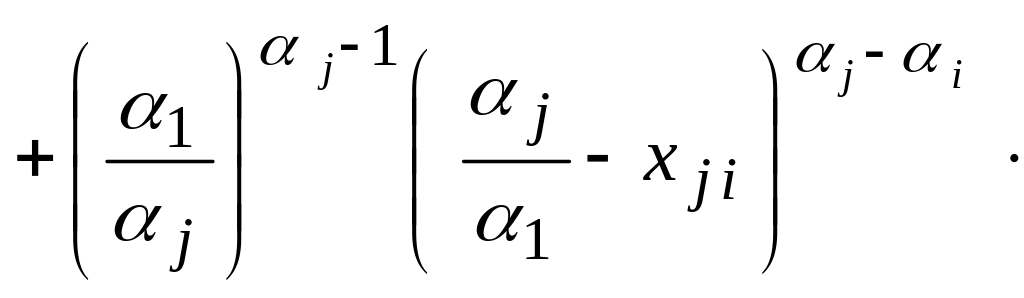
(3.14)

при .

Так как поправка, вносимая -м сервером в -е решение сдвигает максимум суммарного риска вправо при , то в этом случае решение будем искать в виде:

.

В нелинейных уравнениях (3.13) и (3.14) разложение экспоненты в ряд Тейлора не приводит к уравнениям, решаемых в радикалах. Поэтому есть смысл решать их численными методами, например, методом Ньютона.

При суммарный риск сдвигается влево, и решение уравнения будем искать в виде:

.

Для системы, включающей m серверов, получим уравнения, где каждая поправка вычисляется для пары серверов [24,56]:

. . .

.

Просуммировав значения элементов, стоящих в соответствующих строках и значения , , получим вектор-столбец для координат, при которых находятся максимумы суммарного риска.

Для удобства анализа представим поправки в виде матрицы поправок [53,56]:

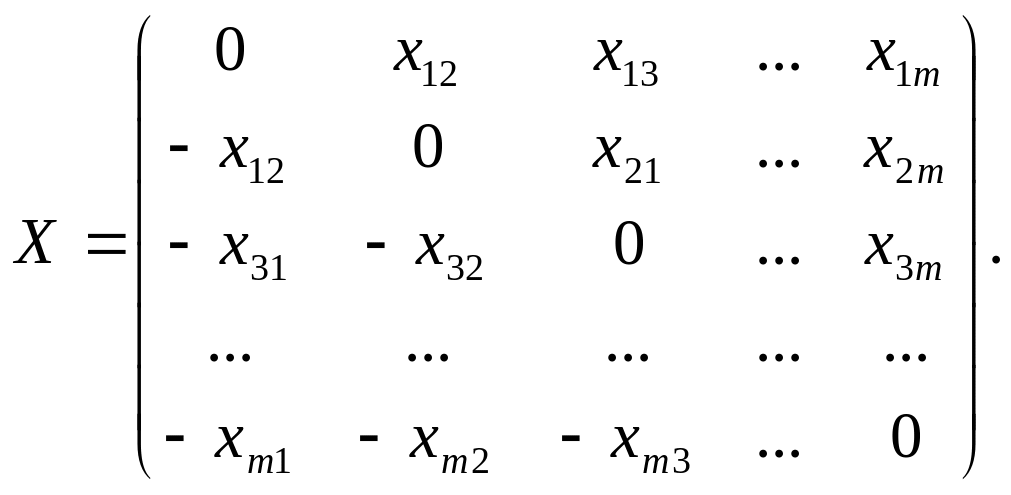
Сумма элементов, стоящих в i-й строке определит поправку для максимального значения в окрестности , то есть, усредненный ущерб, полученный в результате реализации атаки на j-й сервер, будет равен:

, .

Таким образом, получаем вектор координат ущербов, при которых суммарная функция риска достигает максимальных значений:

, .

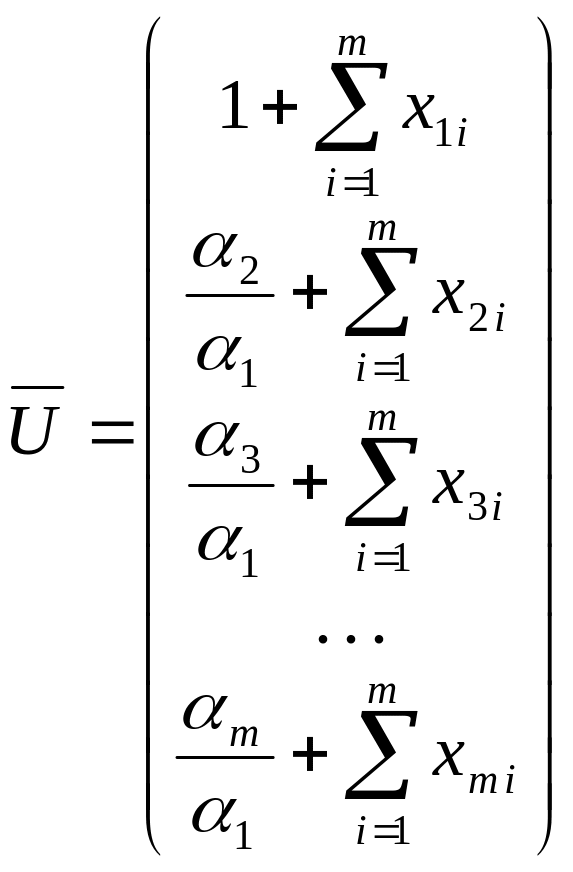При формировании алгоритма противодействия DDoS-атакам на МСС предпочтительно использовать универсальные параметры системы, которые легко доступны и не увеличивают нагрузку на сервер при их получении. В связи с этим, при минимизации интегрального риска актуальным становится получение значений его максимумов и минимумов через параметры компонентов системы. Важна здесь и обратная задача: найденные поправки для установки экстремумов позволяют при необходимости скорректировать значения исходных параметров компонентов МСС таким образом, чтобы функция интегрального риска колебалась в заданной полосе неравномерности.