Ситуации равновесия в игре.

Если V_A – цена игры, то V <= V_A <= V

В любой матричной игре V <= V

Оптимальной в игре считают такую ситуацию, от которой не выгодно отклоняться обоим игрокам. Такая ситуация называется равновесной.

Пусть (A*_i, B*_j) – ситуация равновесия, оптимальная. Она является равновесной, если a_ij* <= a_i*j* и a_i*j >= a_i*j* Здесь a_i*j* = V_a – цена игры. i*, j* - оптимальные стратегии A и B.

Понятие седловой точки.

Седловая точка – это пара оптимальных стратегий (A_i, B_j). В этом случае число a=b называется (чистой) ценой игры (нижняя и верхняя цена игры совпадают). Это означает, что матрица содержит такой элемент, который является минимальным в своей строке и одновременно максимальным в своем столбце.

Чистые стратегии двух игроков.

Теорема: если в матричной игре существует a_i*j* (седловая точка), то говорят, что матричная игра имеет решение в чистых стратегиях: V = V

Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.

Оптимальные чистые стратегии игроков отличаются от смешанных наличием обязательного единичного p_i = 1, q_i = 1. Например: P(1,0), Q(1,0). Здесь p₁ = 1, q₁ = 1.

Смешанные стратегии двух игроков в матричной игре.

Если в матричной игре не существует ситуации равновесия, то V <= V и игрокам не выгодно придерживаться своих максиминных стратегий. Получение выигрыша можно достичь путем случайного применения стратегий.

Случайная величина, значениями которой являются стратегии игрока, называется его смешанной стратегией.

Пусть (m x n) – игра, тогда смешанная стратегия игрока А определяется как вектор x = (p₁, p₂, …, p_m). 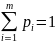и p_i – вероятность выбора игроком А его i-той стратегии.

При выборе стратегии A_i x = (0, 0, … 0, 1, 0, …, 0)

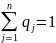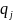Для игрока В все аналогично: y = (q₁, q₂, …, q_n) и – вероятность выбора игроком B его j-той стратегии.

Выигрыши игроков в игре.

Определим функцию выигрыша:

В ситуации (A_i, B_j) игрок А получает A_ij*p_i*q_j.

В ситуации (x, y) А получает H_A (xy) = V_A(xy) = V(xy) =

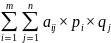
Теорема Дж. фон Неймана о ситуации равновесия.

Ситуация (x* y*) – является ситуацией равновесия в матричной игре mn, а

v_a = v(x* y*) – цена игры для любых x, y: v(x y*)<= v(x* y*)<= v(x* y) – оптимальная ситуация в смешанных стратегиях.

Теорема: В любой матричной игре существует хотя бы одна ситуация равновесия в смешанных стратегиях.

Аналитическое решение игры 22.

Для аналитического решения необходимо составить систему из двух уравнений, где коэффициенты между p и q это элементы, соотв. одной из двух стратегий игрока A (или В).

Решив систему можно найти p (или q), x*(y*), а так же v.

Геометрическое решение игры 22.

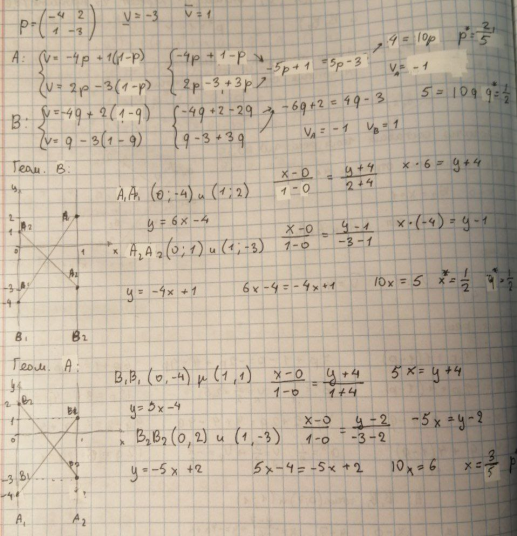
Лемма о масштабе.

Пусть имеется 2 матричных игры p и p’: :

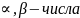
где v – цена игры матрицы Р.

При этом x’ = x, y’ = y.

Иными словами, две игры, отличающиеся лишь началом отчета выигрышей и масштабом их измерения, стратегически эквивалентны.

Условия эквивалентности смешанных стратегий двух игр – мы все хз.

1. x* (p₁*, … p_m*), y* (q₁*, … q_n*) – оптимальные смешанные стратегии игроков A и В.

x* составляется только из таких A_i, для которых

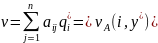
Аналогично для В: B_j такие, что

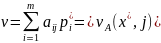
2. Для того, чтобы (x* y*) была ситуацией равновесия необходимо и достаточно, чтобы v_A(i, y*) <= v <= v_A(x*, j)

3. Для того, чтобы (x* y*) была ситуацией равновесия необходимо и достаточно, чтобы max v_A(i, y*) = min v_A(x*, j)

4. В матричной игре множество оптимальных ьсмешанных стратегий А и В является выпуклым многогранником

5. Если матрица Р является косиметричной (a_ij = -a_ji), v = 0 и x* = y* (множества)

6. Для любого i при котором v_A (i, y*) < v, p_i* = 0. Аналогично для игрока В.

В соответствии с теоремой фон-неймона и свойством 3, в любой матричной игре всегда выполняется соотношение: v = max min v(x, j) = min max v (i, y).

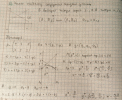
Пусть x* (p₁*, … p_m*), y* (q₁*, … q_n*) векторы оптимальных стратегий игроков, тогда чистая стратегия (i) игрока A или чистая стратегия (j) игрока B называется существенной, активной, если p_i* > 0 (q_j* > 0).

Игроки не могут отказаться от своих существенных стратегий.

Теорема 1: Если один игрок придерживается оптимальной стратегии, то его соперник достигает цены игры ν, применяя любую свою смешанную стратегию, в которой используются только активные стратегии.

Теорема 2: Если один из участников матричной игры G (MXN), придерживается своей оптимальной смешанной стратегии, то это обеспечивает ему максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий (т. е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях), причем число активных стратегий каждого игрока, входящих в их оптимальные смешанные стратегии, не превосходит L, где L = min(m, n).

• A_i стратегия игрока A доминирует его чистую стратегию A_L, если a_ij >= a_Lj при L = от 1 до n. (Строка i доминирует, если её элементы больше)

• Чистая стратегия B_j доминирует его чистую стратегию B_k, если a_ij <= a_ik при k = от 1 до m. (столбец j доминирует, если его элементы меньше)

• В (m x n) игре i стратегия игрока А дублирует его j стратегию, если a_iL = a_jL при L = от 1 до n. (одинаковые строки)

• В (m x n) игре i стратегия игрока B дублирует его j стратегию, если a_Li = a_Lj при L = от 1 до m. (одинаковые столбцы)

• Все дублирующиеся стратегии кроме одной необходимо удалить.

• A и B не должны использовать свои доминируемые стратегии в игре. Соответствующие строки и столбцы должны удаляться из матрицы P.

В смешанных стратегиях:

• Говорят, что x’ игрока A доминирует его смешанную стратегию x’’, если для всех чистых стратегий игрока В: x’*a^j >= x” * a^j где a^j - j столбец матрицы.

• Аналогично для В

Теорема: Пусть в m x n игре i-я строка/j-ый столбец матрицы p доминируем. Пусть p’ – матрица, получаемая из р вычеркиванием доминируемых строк/столбцов. Тогда:

1. Цены игр совпадают

2. Любая оптимальная стратегия y’ игрока B в матрице p’ является оптимальной и в матрице р (Аналогично для игрока А)

3. Если x’ – оптимальная смешанная стратегия игрока А в игре с матрицей p’, то оптиамльная смешанная стратегия x’ игрока А в игре с матрицей p получится из x’ добавлением на i-е место в векторы x’ нуля (Аналогично для игрока В).

Пусть все стратегии обоих игроков или хотя бы у одного из них будут активными (существенными) и при этом ни одна из существенных стратегий не является строго доминируемой. Такую ситуацию равновесия (x* , y* ) в игре принято называть вполне смешанной (т.е. хотя бы у одного из игроков все вероятности pi (q j ) ненулевые по  i, j ).

Теорема. Если матричная (m * n)-игра является вполне смешанной и цена игры v не равна 0 , то игра имеет единственное решение и квадратную матрицу ( m = n ). При этом, оптимальные стратегии (x* , y* )определяются по следующим формулам:

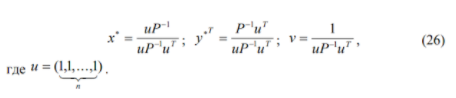
Комментарий к теореме: если матрица P содержит отрицательные элементы, то ее цена игры может оказаться равной нулю. Тогда, чтобы использовать формулы (26), нужно изменить матрицу P , прибавив к ее элементам любое положительное число a , такое, чтобы все элементы стали положительными. Этим мы гарантируем выполнение условия: v не равно 0 . В соответствии с леммой о масштабе, оптимальные стратегии для игры с новой матрицей P* = P +a   будут такими же, как и в игре с матрицей P .

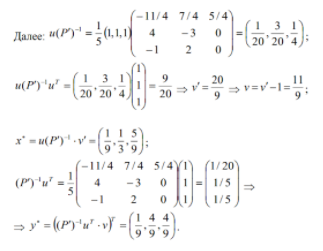
Пусть дана конечная матричная игра с платежной матрицей А размера тхп без седловой точки. Без ограничения общности будем считать, что элементы платежной матрицы положительны, тогда цена игры у также положительна. Рассмотрим последовательно стратегии первого и второго игроков.

Стратегия игрока М.

При любой стратегии Nj игрока N оптимальная смешанная стратегия х = (Xj, х2, ..., хт) игрока М обеспечит его средний выигрыш не меньше у, т. е. выполняется:

Введем обозначение С учетом этого получим:

Поскольку игрок M стремится максимально увеличить свой гарантированный выигрыш, задача сводится к отысканию такого вектора и = (и1г и2, ..., um)', чтобы

где b = (1, 1, 1)' — /n-вектор, при условии

где с = (1, 1, 1)' — /г-вектор,

Таким образом, для получения оптимального решения для игрока М необходимо решить задачу линейного программирования .

Стратегия игрока N.

Аналогично для игрока N, оптимальная смешанная стратегия у = (у1г у2, ..., у„) при любом выборе игроком М своих стратегий М, обеспечит проигрыш игроку N не больше у:

Обозначив

получим:

Поскольку игрок N стремится сделать свой гарантированный проигрыш минимальным, задача сводится к отысканию такого и = (и1; и2,..., о,,)', для которого выполняется:

при условии:

Рассмотренные для игроков задачи представляют собой пару двойственных задач линейного программирования. Сформулируем полученный результат в виде теоремы [36].

Теорема. Решение матричной игры с положительной платежной матрицей

где аи > 0 равносильно решению пары двойственных задач линейного программирования:

гдеЬ = (1,1,1)' — m-вектор, с = (1,1,1)' — п-вектор.

Решение матричной игры (я*, г/*, у) связано с решением (и*, нх) пары двойственных задач следующими соотношениями:

Неантагонистические

В случае игры двух лиц игра называется неантагонистической, если пересечение интересов этих игроков может приводить к ситуациям, выгодным обоим игрокам. В неантагонистических играх различают бескоалиционное поведение, когда соглашения между игроками запрещены правилами, и кооперативное (коалиционное) поведение игроков, когда разрешается кооперация (объединение игроков в группы) типа выбора совместных стратегий и совершения побочных платежей. 

Система Г = N, {Xi}i∈N, {Hi}i∈N, в которой N {1, 2, ...,n} - множество игроков, Xi – множество стратегий i -го игрока, Hi – функция выигрыша i -го игрока, определенная на декартовом произведении множеств стратегий игроков X = X1*X2*...*Xn (множество ситуаций в игре), называется бескоалиционной игрой. 

В бескоалиционной игре n лиц игроки выбирают свои стратегии i Xi x  независимо друг от друга, в результате чего формируется ситуация в игре x = (x1,x2,...,xn) и каждый игрок получает выигрыш, равный Hi(x). 

Если множества Xi чистых стратегий игроков конечны, то игра называется конечной бескоалиционной игрой n лиц. 

Биматричные

Биматричной игрой называется конечная бескоалиционная игра двух лиц. Пусть игрок A имеет m стратегий, а игрок B – n стратегий. Тогда биматричную игру можно описать двумя матрицами выигрышей A и B для игроков A и B :

или в виде матриц: А = (аij)mxn, B = (bij)mxn. 

Здесь aij – выигрыш игрока A, если он применит свою стратегию Ai, а игрок B – стратегию Bj, т.е. в ситуации (Ai, Bj); bij – выигрыш игрока B в ситуации (Ai, Bj). Это задает биматричную игру в нормальной форме. 

Итак, если интересы игроков A и B не совпадают, но не обязательно противоположны, получаются две платежные матрицы: матрица A – матрица выплат игроку A , другая матрица B – матрица выплат игроку B . Поэтому название игры здесь совершенно естественно – биматричная.

Матричную игру можно считать частным случаем биматричной игры, когда матрица выплат игроку B противоположна матрице выплат игроку A :

bij = -aij или B = -A

В общем случае биматричная игра – это игра с ненулевой суммой.

Функии выигрыша

Как и в случае матричных игр, в биматричных играх ситуация равновесия (в чистых стратегиях) существует не всегда. Можно прийти к смешанному расширению игры, предполагая, что каждая игра может быть повторена в неизменных условиях. При этом средние выигрыши игроков А и В определяются по их платёжным матрицам через следующие функции выигрыша:

где x = (p1,p2,…,pm) - вектор смешанной стратегии игрока А, причём

pi ≥ 0, i = 1,m; а также y = (q1, q2,...,qn) - вектор смешанной стратегии игрока В, в котором

Ситуация ( i* , j* ) биматричной игры называется ситуацией равновесия (равновесной по Нэшу) в чистых стратегиях, если aij* ≤ ai*j* для i от 1 до m и bi*j ≤ bi*j* для j от 1 до n (т. е. отклонение от равновесной стратегии не увеличивает выигрыш игрока) Для того чтобы найти ситуацию равновесия по Нэшу в чистых стратегиях, необходимо найти в каждом столбце матрицы выигрышей игрока A максимальный элемент и подчеркнуть его. Аналогично, в каждой строке матрицы выигрышей игрока B нужно подчеркнуть максимальный элемент. Если в обеих матрицах будет подчеркнут элемент, стоящий на одном и том же месте, то его положение и определит ситуацию равновесия в игре.

В биматричных играх, как и в матричных, можно использовать принцип (строгого) доминирования для удаления заведомо невыгодных стратегий у игроков A и B

Нахождение равновесия Нэша в смешанных стратегиях:

Положим:

C = a11 -  a12 -  a21 +  a22 ,

α = a22 -  a12 , 

D =  b11 -  b12 -  b21 +  b22 ,

β = b22 -  b21 .

Для игрока A:

Если C = α = 0 то решением будет являться весь единичный квадрат p∈[0,1], q∈[0,1]

Если C = 0, α ≠ 0 , то решением является либо p = 0 , либо p = 1

Если C > 0 , то получим следующие решения: 

1) если p = 0 , то q ≤ α/С

2) если p = 1 , то q ≥ α/С

3) если 0 < p < 1 , то q = α/С

Если C < 0 , то решения будут следующие:

1) если p = 0 , то q ≥ α/С

2) если p = 1 , то q ≤ α/С 

3) если 0 < p < 1 , то q = α/С

Графическая интерпретация множества решений игрока A :

Для игрока B алгоритм тот же самый, только нужно поменять буквы C на D, p на q, α на β

Графическая интерпретация множества решений игрока B:

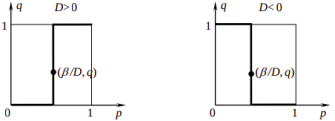
Решением игры является пересечение множеств решений для игроков A и B. Графически решение будет выглядеть как пересечение двух зигзагов, варианты которых приведены на рисунках выше. При этом эти зигзаги могут быть как противоположными, так и одинаковой направленности. В первом случае мы получим три точки пересечения, т.е. три состояния равновесия, а во втором – одну. Причем решения в углах квадрата - решения в чистых стратегиях.

Нахождение равновесия Нэша в смешанных стратегиях:

Положим:

C = a11 -  a12 -  a21 +  a22 ,

α = a22 -  a12 , 

D =  b11 -  b12 -  b21 +  b22 ,

β = b22 -  b21 .

Для игрока A:

Если C = α = 0 то решением будет являться весь единичный квадрат p∈[0,1], q∈[0,1]

Если C = 0, α ≠ 0 , то решением является либо p = 0 , либо p = 1

Если C > 0 , то получим следующие решения: 

1) если p = 0 , то q ≤ α/С

2) если p = 1 , то q ≥ α/С

3) если 0 < p < 1 , то q = α/С

Если C < 0 , то решения будут следующие:

1) если p = 0 , то q ≥ α/С

2) если p = 1 , то q ≤ α/С 

3) если 0 < p < 1 , то q = α/С

Графическая интерпретация множества решений игрока A :

Для игрока B алгоритм тот же самый, только нужно поменять буквы C на D, p на q, α на β

Графическая интерпретация множества решений игрока B:

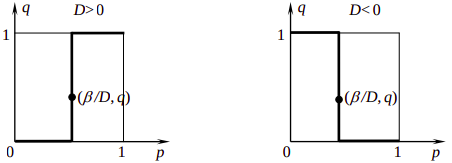
Решением игры является пересечение множеств решений для игроков A и B. Графически решение будет выглядеть как пересечение двух зигзагов, варианты которых приведены на рисунках выше. При этом эти зигзаги могут быть как противоположными, так и одинаковой направленности. В первом случае мы получим три точки пересечения, т.е. три состояния равновесия, а во втором – одну. Причем решения в углах квадрата - решения в чистых стратегиях.

Сильно равновесные стратегии.

Ситуация {x*,y*} называется сильно равновесной(в смешанных стратегиях) в биматричной игре, если в формуле ниже все неравенства строгие:

HA(x,y*)HA(x*,y*), HB(x*,y)HB(x*,y*)

В оптимальной по Парето ситуации, все игроки, действуя совместно, не могут увеличить выигрыш каждого, не уменьшив при этом выигрыш одного из них. 

Например, в дилемме заключенного оптимум по Парето достигается, когда оба заключенных молчат.

В матричных играх 2x2 надо сначала найти точку утопии T. Точка утопии это точка, в которой значения выигрышей игроков максимальны. 

Далее в координатах выигрышей первого и второго игроков строим множество всех возможных решений.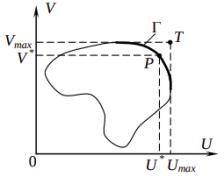

На рисунке множество Парето выделено жирным. Эти точки такие, что нельзя перейти в другую точку множества решений, не уменьшив один из выигрышей.

Оптимум по Парето находится в точке P - в ближайшей точке множества Парето к точке утопии. 

Множество допустимых решений задается функциями выигрыша U = Ha(p, q) и V = Hb(p, q), но так как они квадратичные, то можно последовательно подставлять значения p и q равными 0 и 1 (всего 4 варианта). Таким образом получаем 4 прямые, учитывая, что 0 ≤ p ≤ 1 и 0 ≤ q ≤ 1, получаем ограничения для прямых.

Пример:

U = 2pq - 3p + 6q -6

V = 2pq + 6p - 3q - 6

1. при p = 0: 

 U = 6q - 6, V = -3q - 6 => V = -1/2U - 9, -6 ≤  U ≤ 0, -9 ≤ V ≤ -6

2. при p = 1:

U = 8q - 9, V = -q => V = -(U + 9)/ 8, -9 ≤  U ≤ -1, -1 ≤ V ≤ 0

3. при q = 0:

U = -3p - 6, V = -6p - 6 => V = -18 - 2U, -9 ≤  U ≤ -6, -6 ≤ V ≤ -0

4. при q = 1:

U = -p, V = 8p - 9 => V =-8U - 9, -1 ≤  U ≤ 0, -9 ≤ V ≤ -1

Строим по прямым и получаем:

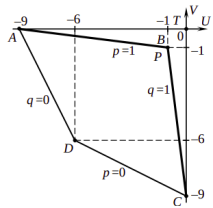
Здесь множество Паретто - AB и BC, точка утопии - T(0, 0), а оптимумом по Паретто будет точка P (-1, -1) так как она ближе всего к точке утопии. Чтобы получить окончательный результат p и q необходимо решить систему U = 2pq - 3p + 6q -6 = -1; V =  2pq + 6p - 3q - 6 = -1 

В результате получаем p*п = 1, q*п = 1

Диллема узников. 

Построим множество Парето и найдем точку оптимальную по Парето.

Выпишем функции выигрышей игроков:

U = HA(p,q) = 2pq - 3p + 6q - 6

V = HB(p,q) = 2pq + 6p - 3q - 6    (1)

0 p ; q 1.

Найдем границы множества точек, удовлетворяющих данным выражениям:

HA(p*,q*) HA(p,q) 

HB(p*,q*) HB(p,q) 

Для этого можно рассматривать крайние значения переменных p и q:

1) При p = 0 имеем: U = 6q - 6; V = -3q - 6, следовательно V = -(U/2) - 9, -6 U 0, -9 V -6.

2) При p = 1 имеем: U = 8q - 9; V = -q, следовательно V = -(U + 9) / 8, -9 U -1, -1 V 0.

3) При q = 0 имеем: U = -3p - 6; V = 6p-6, следовательно V = -18 -2U, -9 U -6, -6 V 0.

4) При q = 1 имеем: U = -p; V = 8p-9, следовательно V = -8U -9, -1 U 0, -9 V -1.

Получился четырехугольник с вершинами в точках A(-9, 0), B(-1,-1), C(0, -9), D(-6,-6):

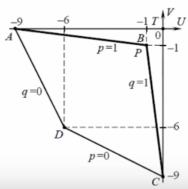
Точка утопии здесь - это точка T(0;0), так как Umax = 0 и Vmax = 0. Множество Парето здесь определяется отрезками прямых при p = 1 и q = 1. Ближайшей точкой множества Парето к точке утопии T является точка P = B(-1;-1), т.е UП*= -1, VП*= -1. Решая систему уравнений  HA=(pП*, qП*) = -1, HB=(pП*, qП*) = -1, находим что pП* = 1, qП* = 1. Это означает, что оптимальной ситуацией по Парето будет ситуация (pП*, qП*) = (1,1). (Игроки A и B принимают свои первые чистые стратегии)

Семейный спор

Найдем оптимальные стратегии по Парето. 

U = HA(p,q) = 3pq - p - q + 1

V = HB(p,q) = 3pq - 2p - 2q + 2    (2)

0 p ; q 1. 

Точка утопии T=(Umax , Vmax)=(2;2). Ближе всех к этой точке будут точки (2,1) и (1,2), т.е ситуации (1,1) и (0,0). Эти ситуации будут оптимальными по Парето в чистых стратегиях. Построим на плоскости 0UV мн-во точек, определяемых U = HA(p,q) и 

V = HB(p,q), где 0 p 1, 0 q 1. 

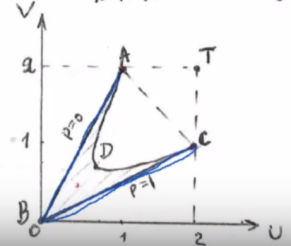
1) При p = 0 имеем: U = 1 - q; V = 2-2q, следовательно q = 1-U => V = 2-2(1-U) = 2U, 0 U 1, 0 V 2. A(1,2) - Ситуация равновесия(0,0). B(0,0) - соответствует ситуации (0,1).

2) При p = 1 имеем: U = 2q; V = q, следовательно q = U/2 => V = U/2, 0 U 2, 0 V 1. C(2;1) - ситуация равновесия (1,1). Точке B соответствует также ситуация (1,0).

3) При q = 0 имеем: U = -1 - p; V = 2-2p, следовательно V = 2U (Линия AB)

4) При q = 1 имеем: U = 2p; V = p, следовательно V = U/2(Линия BC)

Кроме того, границей мн-ва точек(U,V) будет кривая ADC, где точка D имеет такие координаты, что UD=VD это значение максимально. Найдем это значение: U = V => 3pq - p - q + 1 = 3pq - 2p - 2q + 2 => p + q = 1 => q = 1 - p => U = 3p(1-p) - p - (1-p) + 1 = 3p - 3p2 => 3p2 - 3p + U = 0.

Решаем это уравнение как параметрическое: p1,2=39-12U6  => Решение существует при 9-12U 0 => U 912=34 . Тогда и V 34. Граница Парето - это лини AC, точки которой, за исключением A,C, не принадлежат множеству возможных значений U V. Если принять U=V= 34, то p = 12 и q = 12. Таким образом, решения в смешанных стратегиях по Парето здесь нет.

Принятие решений в статистических играх в условиях полной определенности, это когда данные известны точно и ЛПР точно знает последствия и исходы любой альтернативы или выбора решения.

Критерий Вальда

Согласно критерию Вальда, наилучшей считается максиминная стратегия.  Это критерий крайнего пессимизма. По этому критерию ЛПР выбирает ту стратегию, которая гарантирует в наихудших условиях максимальный выигрыш:

Чтобы найти критерий Вальда, требуется найти минимальные элементы в каждой строке, затем среди найденных минимальных значений выбрать максимальный элемент, этот элемент будет соответствовать наилучшей стратегии по критерию Вальда.

Критерий Сэвиджа

Критерий Сэвиджа (критерий потерь от «минимакса») предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая минимизирует размеры максимальных потерь по каждому из возможных решений. При использовании этого критерия «матрица решения» преобразуется в «матрицу риска», в которой вместо значений эффективности проставляются размеры потерь при различных вариантах развития событий.

Матрица риска находится по формуле:

Критерий Сэвиджа находится по формуле:

Критерий Гурвица

Критерий Гурвица (критерий «оптимизма-пессимизма») позволяет руководствоваться при выборе рискового решения в условиях неопределенности некоторым средним результатом эффективности, находящимся в поле между значениями по критериям «максимакса» и «максимина» (поле между этими значениями связано посредством выпуклой линейной функции).

Критерий Гурвица находится по формуле:

 

ММ-критерий

Правило выбора для этого критерия формулируется следующим образом. Матрица решений дополняется еще тремя столбцами.

1. Математическое ожидание каждой из строк.

2. Разность между опорным значением ei0j0 = maxi(minj(eij)) и наименьшим значением minj(eij) соответствующей строки.

3. Разности между наибольшим значением maxj(eij) каждой строки и наибольшим значением maxj(ei0j) той строки, в которой находится значение ei0j0.

Выбираются те варианты, строки которых дают наибольшее математическое ожидание.

Критерий Байеса

Если вероятности q_i  состояний природы известны, то пользуется критерий Байеса, в соответствии с которым оптимальной считается чистая стратегия , при которой максимизируется средний выигрыш:

Критерий Лапласа

Если игроку А представляются в равной мере правдоподобными все состояния природы, то иногда полагают q₁= … = q_­n­ = 1/n  и, учитывая, «принцип недостаточного основания» Лапласа, оптимальной считают чистую стратегию A_i, обеспечивающую:

Критерий Ходжа-Лемана

Этот критерий опирается одновременно на ММ-критерий и критерий Баеса-Лапласа. С помощью параметра V выражается степень доверия к используемому распределений вероятностей. Если доверие велико, то доминирует критерий Баеса-Лапласа, в противном случае — ММ-критерий

Где 0 <= V <= 1 – степень доверия к функции распределения вероятностей

При V = 1 – минимальный критерий

При V=0 – критерий Байеса-Лапласа

Позиционная игра – это игра, моделирующая процессы последовательного принятия решений в условиях меняющейся во времени и неполной информации.

Состояния игры называют позициями, возможные выборы в каждой позиции – альтернативами.

Одноэтапные игры с природой удобно использовать в задачах, имеющих одно множество альтернативных решений и одно множество состояний среды. Позиционные игры, однако, требуют анализа последовательности решений и состояний среды, когда одна совокупность стратегий игрока и состояний природы порождает другое состояние подобного типа. Если имеют место два (или более) последовательных множества решений, причем последующие решения основываются на результатах предыдущих, и/или два (или более) множества состояний среды (т.е. появляется целая цепочка решений, вытекающих одно из другого, которые соответствуют событиям, происходящим с некоторой вероятностью), используется дерево решений.

Дерево решений – это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды.

Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение пяти этапов:

1. Формулирование задачи. 

2. Построение дерева решений. Оно состоит из двух основных частей: «решений» и «вероятностных событий.

3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события. Указанные вероятности определяются либо на основании имеющейся статистики, либо экспертным путем.

4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды.

5. Решение задачи.

Дерево решений состоит из ряда узлов и исходящих из них ветвей. Квадраты обозначают пункты принятия решений (или возможные события), а дуги соответствуют переходам между логически связанными решениями и случайными событиями. Из вершины-решения (квадратов) исходит столько дуг, сколько имеется вариантов (альтернатив), выбор конкретной дуги (вариант решения) осуществляется ЛПР. Из вершины-события также может исходить несколько дуг. Но здесь уже выбор осуществляется случайным образом в соответствии с заданными вероятностями отдельных исходов.

После того, как дерево решения построено, оно анализируется справа налево, т.е. начинать надо с последнего принятого решения. Для каждого решения выбирается альтернатива с наибольшим показателем отдачи (или с наименьшими затратами). Если за принятием решения следует несколько возможных вариантов событий, то выбирается альтернатива с наибольшей предполагаемой прибылью (или с наименьшей предполагаемой величиной затрат).

Различают следующие виды позиционных игр:

 - позиционные игры с полной информацией, в которых каждый игрок при своем ходе знает ту позицию дерева решений, в которой он находится;

- позиционные игры с неполной информацией, где игрок, делающий ход, не знает точно, в какой именно позиции дерева решений он фактически находится. Этому игроку известно лишь некоторое множество позиций, включающее в себя его фактическую позицию. Такое множество позиций называется информационным множеством.

Позиции, принадлежащие одному и тому же  информационному множеству, объединяются пунктирными линиями.  В каждое информационное множество входят только неразличимые для игрока узлы, т. е. только те узлы, для каждой пары из которых соответствующий игрок не может точно указать, в какой точке дерева он находится, делая этот ход.

Составляя информационные множества, следует помнить следующее:

(а) в одно информационное множество могут входить только узлы, относящиеся к одному игроку;

(б) любая линия игры (ветвь дерева, отображающая партию игры) не должна пересекать одно и то же информационное множество больше одного раза.

Условие (б) можно сформулировать еще так: в одно информационное множество не должно входить больше одного узла каждой ветви, отображающей партию игры.

Процесс сведения позиционной игры к игре в нормальной форме называют нормализацией игры. Любая позиционная игра может быть сведена к игре в нормальной форме, в которой каждый из игроков делает только по одному независимому ходу. Для нормализации игры нужно перечислить все возможные стратегии игроков и для каждой совокупности стратегий определить выигрыш игроков.