Для задачи на максимум

• Смотрим на коэффициенты в функции F(x). Если есть положительные, значит решение не оптимально. Переменную с наименьшим коэффициентом необходимо вывести из базиса.

• Подставим в систему ограничений выводимую переменную как 0 и найдем значения оставшейся переменной. Выберем минимальное или то, на которое нет ограничений.

• Затем введем базис переменную, соответствующую ограничению, которое мы выбрали на предыдущем шаге.

• Пересчитаем систему ограничений, выразив выводимую и вводимую переменные. Пересчитаем так же F(x). выпишем X⁽¹⁾ .

• Если в F(x) присутствуют не отрицательные коэффициенты, изменим базис снова, повторив вышеописанные действия.

• Когда наконец получена F(x), где все коэффициенты отрицательны – мы получили оптимальное решение. X* = X⁽ⁿ⁾

Для задачи на минимум

Все аналогично, однако при задаче на минимум в оптимальном решении в F(x) все коэффициенты должны быть положительными,

Для решения ЗЛП при помощи симплекс-таблицы необходимо в начале представить ЗЛП в каноническом виде, затем выбрать допустимый базис и свободные переменные и начертить таблицу:

• В столбце б названы переменные базиса.

• В столбце С_б – их коэффициенты в F(x).

• В столбце X_б значения из системы ограничений.

Далее идут столбцы переменных.

• Столбцы переменных базиса являются столбцами единичной матрицы (хоть впоследствии они и не будут идти по порядку)

• Столбцы свободных переменных в начале заполняются в соответствии со значениями матрицы A (коэффициенты из системы ограничений)

После заполнения таблицы следует подсчитать дельты:

• ₀ вычисляется как сумма произведений X_б на С_б

• Дельты для свободных переменных вычисляются

  • В задачах на максимум

как сумма произведений X_j на С_б - C_j

• В задачах на минимум

как C_j - сумма произведений X_j на С_б

Если хотя бы одна дельта отрицательна – решение не оптимально.

• Находим переменную, дельта которой отрицательна и наибольшая по модулю.

• Считаем ограничения для этой переменной.

Ограничения сичтаются по следующим правилам:

• Если a_il и б_i имеют разные знаки, то ставится –

• Если a_il = 0 или б_i = 0 то ставится –

• В противном случае ограничение вычисляется по формуле б_i/ a_il

• Выбираем переменную, у которой минимальное ограничение. Её необходимо вывести из базиса.

Строка выводимой переменной и столбец вводимой в базис переменной называются разрешающими.

На их пересечении находится разрешающий элемент.

Строим следующую симплекс-таблицу:

• Столбцы не меняют свой порядок, как и строки. Однако, в разрешающей строке из прошлой таблицы переменная должна измениться на ту, что мы ввели в базис.

• Значения в этой строке переписываются равными значениям из предыдущей таблицы той же строки, но делятся на разрешающий элемент.

• Строки и столбцы, в пересечении с которыми в разрешающих строке и столбце предыдущей таблицы стоял 0, переписываются без изменений (кроме дельт).

• В столбец новой базисной переменной должен быть аналогичен столбцу старой.

• Дельты базисных переменных все также должны равняться 0.

• Наконец, столбец С_б необходимо обновить, если необходимо.

• Все остальные значения таблицы подсчитываются по формуле:

a^(t+1)_ij = a^(t)_ij – (a^(t)_il* a^(t)_kj)/( a^(t)_kl) (те старое значение клетки минус перемноженные пересечения с разрешающими, деленные на разрешающий элемент)

После заполнения очередной таблицы необходимо посчитать дельты и проверить на наличие отрицательных. Если они есть – необходимо повторить с шага про подсчет ограничений. Если нет – решение оптимально.

Метод искусственного базиса так же называется М-метод. Он необходим в тех случаях, когда после добавления новых переменных (для приведения ЗЛП к каноническому виду) все элементы базиса отрицательные.

В таких случаях можно добавить в каждое уравнение, дающее отрицательные компаненты, новые искусственные переменные. В таком случае у нас будет новая функция, равная

В случае задачи на минимум: T(x) = F(x) + M (x_n+1, … x_n+k)

В случае задачи на максимум: T(x) = F(x) - M (x_n+1, … x_n+k)

Где M – большое положительное число, большее, чем любое C_i

Как только все искусственные переменные станут свободными, остальные дадут оптимальное решение.

T_max = F_max

Если хотябы одна искусственная переменная в оптимальном решении не равна 0, то T_max –> -inf, T_min –> inf

Симплекс таблицу составляем и решаем как обычно, разве что базис начинается с искусственных переменных.

Двойственные задачи имеют следующий вид:

Задача 1:

Задача 2: 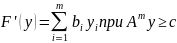Имея задачу, можно составить двойственную к ней задачу. При этом если одна из двойственных друг другу задач имеет оптимальное решение, значит, его имеет и другая. Кроме того, F_max = Z_min т.е. F(x*) = Z(y*)

Вот пример получения двойственной задачи к данной задаче:

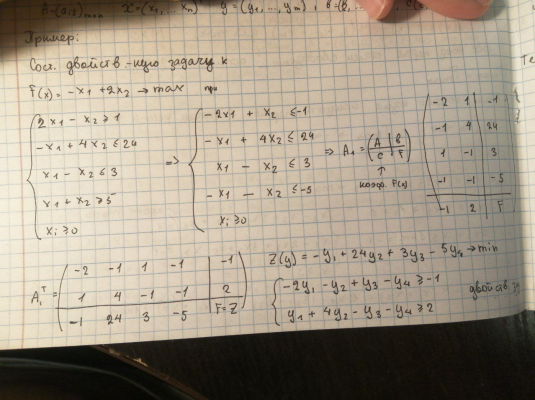
Чтобы из решения одной задачи можно было получить и решение второй, необходимо привести обе задачи в канонический вид.

Теорема 1

Положительным (не нулевым) компонентам оптимального решения одной из двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.

Теорема 2

Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при сопутствующих переменных линейной функции и сходной задачи, выраженных через свободные переменные её оптимального р ешения. Т.е. при решении F(x) y*_j = _n+j Иначе – x*_I = _n+j­­­.

Парные игры с нулевой суммой называются антагонистическими играми.   

Лемма. В любой матричной игре максимин всегда меньше или равен минимакса

Теорема. Если в матричной игре существует седловая точка ( , )   i j , то говорят, что она имеет решение в чистых стратегиях. 

 

Теорема (Дж. фон Нейман). В любой матричной игре существует хотя бы одна ситуация равновесия в смешанных стратегиях.

 

Игра полковника Блотто:

Поле сражения состоит из 5 боевых позиций. У полковника Блотто есть армия из 100 танков, ровно столько же – у его противника. Перед сражением они должны независимо друг от друга расставить свои войска по боевым позициям. На каждой боевой позиции побеждает та сторона, у которой больше танков (в случае ничьей очки за поле делятся пополам). В сражении побеждает та сторона, которая выиграла больше боевых позиций