Задача линейного программирования в канонической форме.

В общем виде ЗЛП выглядит так: А ограничение на переменные так:

Чтобы привести ЗЛП в каноническую форму, необходимо преобразовать неравенства в уравнения, добавив в каждое в левую часть дополнительные переменные.

Тогда в канонической форме ЗЛП будет иметь вид

Множество всех допустимых решений является выпуклым множеством:

Возьмем выпуклые комбинации X₁ X₂

Х₃ – решение

Решение всегда находится на границе.

Основные теоремы о множествах оптимальных решений этой задачи.

Теорема 1: Если задача ЛП имеет оптимальное решение, то линейная функция F(x) достигает своего оптимума (max/min) в одной из угловых точек многогранника решений.

Теорема 2: Каждому допустимому базисному решению ЗЛП соответствует угловая точка многогранника решений и на оборот, каждой угловой точке соответствует допустимое базисное решение. n>m

ЗЛП можно решить геометрически, если m – n = 2. Известно, что m линейных независимых уравнений можно решить через m базисных переменных, выразив их через остальные переменные.

Например x₁, x₂ – свободные, x₂, x₃, x₄, … x_n – базисные

F(x) = c₁x₁ + … + c_nx_n –> max(min) AX = B

Система ограничений состоит из m уравнений, или (если нет – преобразовать) неравенств.

Необходимо построить многоугольник решений в плоскости x₁D x₂. Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F = с₁х₁ + с₂х₂ принимает максимальное (или минимальное) значение. Рассмотрим так называемую линию уровня линейной функции F, т.е. линию, вдоль которой функция принимает одно и то же фиксированное значение а, т.е. F = а, или с₁х₁ + с₂х₂ = a.

Линии уровня перпендикулярны grad F(x), где grad F(x) {с_1, с₂}, направление возрастания, а -grad F(x) – направление убывания.

Точка А, являющаяся оптимальным решением, будет соответствовать точке, через которую проходит линия уровня с максимальным (для задач на максимум) или минимальным (для задач на минимум) уровнем.

Оптимальное решение может не существовать, если многоугольник решений не органичен сверху (для задач на максимум) или снизу(для задач на минимум).

Пример для задачи m X 2 (на максимум и минимум).

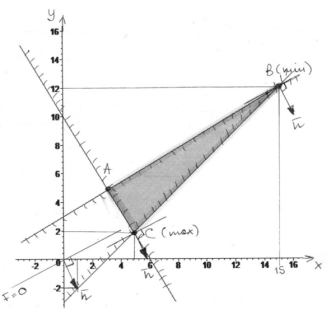
При решении ЗЛП с помощью симплекс метода, задача должна иметь вид

F(x) = … -> max/min + система ограничений вида A*x ? B, где A=(a_ij)_{m x n} – матрица, а x и В – вектора ? – знак неравенства.

Процесс решения:

• Для начала необходимо перевести ЗЛП в канонический вид:

Если система ограничений представлена в виде неравенств, необходимо в каждое уравнение добавить новую переменную в правую часть, чтобы сделать неравенство равенством. (Если знак <= переменная с плюсом, если >=, то с минусом).

• Затем нужно взять 2 переменные свободными, а остальные добавить в базис.

• Базисные переменные в системе ограничений и в F(x) нужно выразить через свободные.

• Чтобы проверить оптимальность, необходимо взять свободные переменные = 0.