17. Смешанные стратегии двух игроков в матричной игре. Выигрыши игроков в игре. Теорема Дж. Фон Неймана о ситуации равновесия. С мешанные стратегии двух игроков в матричной игре.

Если в матричной игре не существует ситуации равновесия, то V <= V и игрокам не выгодно придерживаться своих максиминных стратегий. Получение выигрыша можно достичь путем случайного применения стратегий.

Случайная величина, значениями которой являются стратегии игрока, называется его смешанной стратегией.

П

i

усть (m x n) – игра, тогда смешанная стратегия игрока А определяется как вектор x = (p₁, p₂, …, p_m).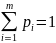 и p_i – вероятность выбора игроком А его i-той стратегии.

При выборе стратегии A_i x = (0, 0, … 0, 1, 0, …, 0)

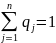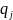Для игрока В все аналогично: y = (q₁, q₂, …, q_n) и – вероятность выбора игроком B его j-той стратегии.

Выигрыши игроков в игре.

Определим функцию выигрыша:

В ситуации (A_i, B_j) игрок А получает A_ij*p_i*q_j.

В ситуации (x, y) А получает H_A (xy) = V_A(xy) = V(xy) =

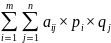
Теорема Дж. фон Неймана о ситуации равновесия.

Ситуация (x* y*) – является ситуацией равновесия в матричной игре mn, а

v_a = v(x* y*) – цена игры для любых x, y: v(x y*)<= v(x* y*)<= v(x* y) – оптимальная ситуация в смешанных стратегиях.

Теорема: В любой матричной игре существует хотя бы одна ситуация равновесия в смешанных стратегиях.

18. Аналитическое решение игры 22. Геометрическое решение игры 22.

Аналитическое решение игры 22.

Для аналитического решения необходимо составить систему из двух уравнений, где коэффициенты между p и q это элементы, соотв. одной из двух стратегий игрока A (или В).

Решив систему можно найти p (или q), x*(y*), а так же v.

Геометрическое решение игры 22.

19. Лемма о масштабе. Условия эквивалентности смешанных стратегий двух игр.

Лемма о масштабе.

Пусть имеется 2 матричных игры p и p’: :

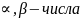
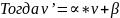где v – цена игры матрицы Р.

При этом x’ = x, y’ = y.

Иными словами, две игры, отличающиеся лишь началом отчета выигрышей и масштабом их измерения, стратегически эквивалентны.

Условия эквивалентности смешанных стратегий двух игр.

20. Свойства оптимальных смешанных стратегий в матричной игре.

1. x* (p₁*, … p_m*), y* (q₁*, … q_n*) – оптимальные смешанные стратегии игроков A и В.

x* составляется только из таких A_i, для которых

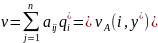
Аналогично для В: B_j такие, что

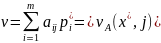
2. Для того, чтобы (x* y*) была ситуацией равновесия необходимо и достаточно, чтобы v_A(i, y*) <= v <= v_A(x*, j)

3. Для того, чтобы (x* y*) была ситуацией равновесия необходимо и достаточно, чтобы max v_A(i, y*) = min v_A(x*, j)

4. В матричной игре множество оптимальных ьсмешанных стратегий А и В является выпуклым многогранником

5. Если матрица Р является косиметричной (a_ij = -a_ji), v = 0 и x* = y* (множества)

6. Для любого i при котором v_A (i, y*) < v, p_i* = 0. Аналогично для игрока В.

В соответствии с теоремой фон-неймона и свойством 3, в любой матричной игре всегда выполняется соотношение: v = max min v(x, j) = min max v (i, y).

21. Графический метод решения матричной игры (2m).

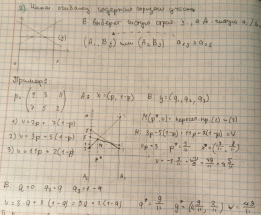
22. Графический метод решения матричной игры (n2).

23. Активные (существенные) стратегии игроков. Теоремы об активных стратегиях.

Пусть x* (p₁*, … p_m*), y* (q₁*, … q_n*) векторы оптимальных стратегий игроков, тогда чистая стратегия (i) игрока A или чистая стратегия (j) игрока B называется существенной, активной, если p_i* > 0 (q_j* > 0).

Игроки не могут отказаться от своих существенных стратегий.

Теорема 1: Если один игрок придерживается оптимальной стратегии, то его соперник достигает цены игры ν, применяя любую свою смешанную стратегию, в которой используются только активные стратегии.

Теорема 2: Если один из участников матричной игры G (MXN), придерживается своей оптимальной смешанной стратегии, то это обеспечивает ему максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий (т. е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях), причем число активных стратегий каждого игрока, входящих в их оптимальные смешанные стратегии, не превосходит L, где L = min(m, n).