13. Метод искусственного базиса в симплекс-методе.
Метод искусственного базиса так же называется М-метод. Он необходим в тех случаях, когда после добавления новых переменных (для приведения ЗЛП к каноническому виду) все элементы базиса отрицательные.
В таких случаях можно добавить в каждое уравнение, дающее отрицательные компаненты, новые искусственные переменные. В таком случае у нас будет новая функция, равная
В случае задачи на минимум: T(x) = F(x) + M (xn+1, … xn+k)
В случае задачи на максимум: T(x) = F(x) - M (xn+1, … xn+k)
Где M – большое положительное число, большее, чем любое Ci
Как только все искусственные переменные станут свободными, остальные дадут оптимальное решение.
Tmax = Fmax
Если хотябы одна искусственная переменная в оптимальном решении не равна 0, то Tmax –> -inf, Tmin –> inf
Симплекс таблицу составляем и решаем как обычно, разве что базис начинается с искусственных переменных.
14. Двойственные задачи линейного программирования. Теоремы двойственности.
Двойственные задачи имеют следующий вид:
Задача 1:
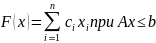
Задача 2:
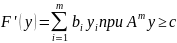Имея
задачу, можно составить двойственную
к ней задачу. При этом если одна из
двойственных друг другу задач имеет
оптимальное решение, значит, его имеет
и другая. Кроме того, Fmax
= Zmin
т.е. F(x*) =
Z(y*)
Вот пример получения двойственной задачи к данной задаче:
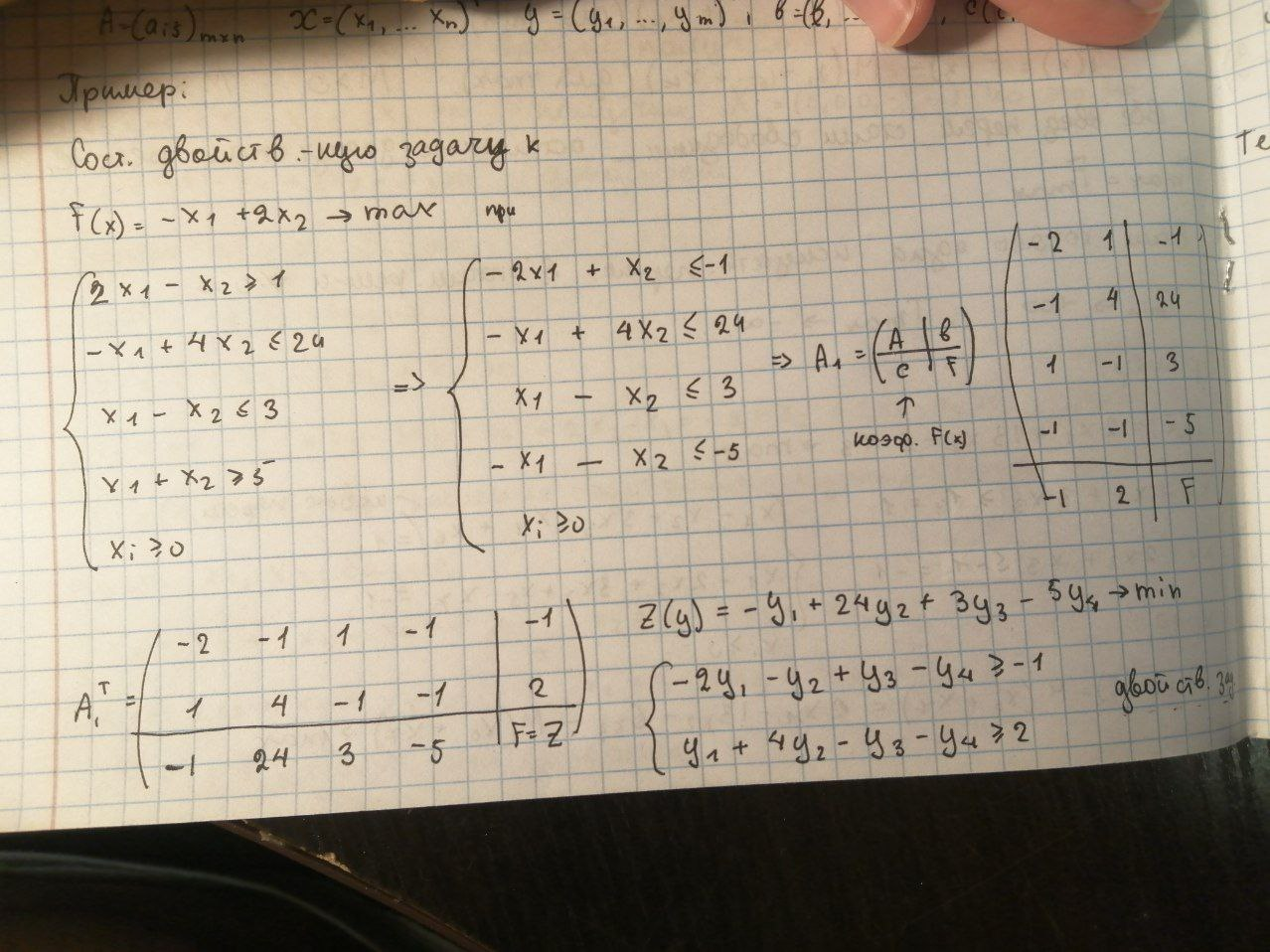
Чтобы из решения одной задачи можно было получить и решение второй, необходимо привести обе задачи в канонический вид.
Теорема 1
Положительным (не нулевым) компонентам оптимального решения одной из двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.
Теорема 2
Компоненты
оптимального решения двойственной
задачи равны абсолютным значениям
коэффициентов при сопутствующих
переменных линейной функции и
сходной
задачи, выраженных через свободные
переменные её оптимального р
ешения.
Т.е. при решении F(x)
y*j =
n+j
Иначе – x*I
= n+j.
15. Антагонистические матричные игры. Примеры игр: игра в монету, поиск, игра полковника Блотто и др. Максимин и минимакс. Выигрыши двух игроков.
Антагонистические матричные игры.
Примеры игр: игра в монету, поиск, игра полковника Блотто и др.
Максимин и минимакс.
Если игрок А выберет свою стратегию Ai, то игрок В ответ на неё такой Bj, для которой PA. Тогда игрок А выберет из всех этих чисел максимальное значение:
V = max(по i) min(по j) - максимин (больше этого игрок А проиграть не может)
А налогично если игрок B выберет свою стратегию Bj, игрок А выберетмаксимум. По этому игрок В может гарантировать для себя проигрыш:
V = min(по j) max(по i) - минимакс (больше этого игрок В проиграть не может)
В ыигрыши двух игроков.
Если VA – цена игры, то V <= VA <= V
В любой матричной игре V <= V
16. Ситуации равновесия в игре. Понятие седловой точки. Чистые стратегии двух игроков.
Ситуации равновесия в игре.
Е сли VA – цена игры, то V <= VA <= V
В любой матричной игре V <= V
Оптимальной в игре считают такую ситуацию, от которой не выгодно отклоняться обоим игрокам. Такая ситуация называется равновесной.
Пусть (A*i, B*j) – ситуация равновесия, оптимальная. Она является равновесной, если aij* <= ai*j* и ai*j >= ai*j* Здесь ai*j* = Va – цена игры. i*, j* - оптимальные стратегии A и B.
Понятие седловой точки.
Седловая точка – это пара оптимальных стратегий (Ai, Bj). В этом случае число a=b называется (чистой) ценой игры (нижняя и верхняя цена игры совпадают). Это означает, что матрица содержит такой элемент, который является минимальным в своей строке и одновременно максимальным в своем столбце.
Чистые стратегии двух игроков.
Т еорема: если в матричной игре существует ai*j* (седловая точка), то говорят, что матричная игра имеет решение в чистых стратегиях: V = V
Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.
Оптимальные чистые стратегии игроков отличаются от смешанных наличием обязательного единичного pi = 1, qi = 1. Например: P(1,0), Q(1,0). Здесь p1 = 1, q1 = 1.