Макроекономіка Радіонова

3 Національна економіка досягла стану загальної (внутрішньої та зовнішньої) рівноваги. Після цього відбулася девальвація національної валюти. Яка політика (фінансова чи грошова) і як

має відреагувати на цю зміну для того, щоб:

а) знову звести торговий баланс з нульовим сальдо

( ∆Nx = 0 );

б) повернутися до виробництва на рівні потенційного продук-

ту ( ∆Y = 0 )?

Зобразьте ситуацію на графіку моделі Nx - (S − I ) .

4 Визначте рівень інфляції за логікою розширеної моделі

торгового балансу, якщо уряд продовжив стимулювання сукупних витрат після досягнення потенційних обсягів випуску. Роз-

рив заощаджень зріс на 20 одиниць, Y * = 250, m′= 0,12, s′ = 0,2. Зобразьте ситуацію графічно.

5 Визначте ефект впливу рівня економічного розвитку

країни за змінами сальдо торгового балансу, спричиненими девальвацією національної валюти. У двох країнах — з вищим і нижчим рівнем розвитку — девальвація спричинила однакові зміни експорту, що оцінюються у 15 одиниць. Схильність до

імпорту в обох країнах однакова: m′ = 0,1 . Схильність до за-

ощаджень є різною — 0,16 та 0,12 відповідно. Зобразьте ситуацію графічно.

1.2.3. Ітераційний (покроковий) рух до загальної рівноваги. Модель Свона

Вступ

Ітераційні моделі є моделями дискретної динаміки. Вони розширили інструментарій макроекономіки завдяки акцентуванню уваги на дослідженні покрокового руху економіки в напрямі загальної рівноваги та на проходженні послідовних станів. Аналіз змісту окремих кроків сприяє уточненню умов і критеріїв ефективного регулювання економіки та обґрунтуванню певних правил державного регулювання.

У цьому підрозділі розглянуто дві ітераційні моделі — динамізовану модель IS-LM та модель Свона.

101

аналізом дискретної послідовності станів ринку в часі. Термін «павутиноподібна модель» (сobweb model) був уведений Н. Калдором у 1934 р. У 1930-х роках інструментарій павутиноподібної моделі був застосований для пояснення цінових коливань на ринках сільськогосподарської продукції та демонстрації принципової можливості виникнення тривалого відхилення ринку від рівноважного стану1.

У працях Я. Тінбергена, Р. Фріша, М. Езекіеля у першій половини ХХ ст. та у працях М. Нерлова, Ф. Воуга, Дж. Мута, Е. Мілза, Р. Фрімена у другій половині ХХ ст. павутиноподібна модель була використана для пояснення впливу очікувань на формування цін та цінових циклів.

Ітераційний підхід почав застосовуватися для пояснення руху економіки до загального рівноважного стану при поєднанні інструментів фінансового і грошового регулювання у працях Дж. Міда, Я. Тінбергена, Т. Свона, В. Салтера, Р. Манделла. Ці дослідники використовували дискретну динамізацію статичних моделей, що створювало додаткові можливості аналізу розподілу ролей між фінансовою та грошовою владою та для визначення правил дій уряду у фінансовій і грошовій сферах.

Основний зміст

Ітераційні моделі посідають своєрідне проміжне місце між моделями порівняльної економічної статики та неперервної економічної динаміки.

Інструментарій порівняльної статики розроблений і успішно застосований у неокласичній теорії, а моделі порівняльної статики мають такі особливості:

пояснюють загальну економічну рівновагу як стан економіки,

що формується внаслідок взаємодії окремих ринків;

представлені системою рівнянь, кожне з яких відображає стан певного структурного елемента економічної системи;

ураховують можливість порушення рівноваги з причин зовнішніх впливів та повернення до неї;

подають розвиток економічної системи як послідовне проходження її рівноважних станів.

Суттєвим обмеженням моделей порівняльної статики є їх непридатність для пояснення нерівноважних станів, що властиві реальній економіці.

1 ФишерС., ДорнбушР., ШмалензиР. Экономика: Пер. сангл. — М.: Дело, 1993. — С. 308.

103

Моделі неперервної економічної динаміки принципово відріз-

няютьсявід моделей порівняльної статики, маючи такі особливості:

•пояснюють рух економічної системи, надаючи проблемі економічної рівноваги другорядного значення;

•акцентують увагу на дослідженні траєкторії економічних змін та на розробці достовірних прогнозів;

•представлені системою диференційних рівнянь, достатніх для відображення змін основних параметрів економічної системи.

Попри те що моделі економічної динаміки розширили пояснювальні можливості економічної науки, їм властиві недоліки, підкреслені, зокрема, Я. Корнаї, А. Клеймером, Д. Макклоскі. Ідеться, зокрема, про те, що при використанні складного математичного апарату економічна наука поступово втрачає своє основне призначення — пояснювати поведінку економічних суб’єктів, перетворюючись унауку, що пояснює «поведінку» змінних урівняннях.

Відносна недосконалість моделей порівняльної статики та неперервної динаміки породила інтерес до ітераційного методу аналізу. Цей метод дає можливість врахувати зовнішні (екзогенні) впливи та ілюструвати їх наслідки. Він ґрунтується на визнанні того, що економіка за одних умов рухається в бік рівноваги, а за інших — віддаляється від неї. У ньому не просто визнається можливість досягнення рівноважного стану, а аналізуються кроки, що забезпечують рух у цьому напрямі. Нарешті, метод дає змогу ілюструвати відгуки економіки на фінансові та грошові імпульси, зумовлені діями уряду.

ринків. При цьому враховуються імпульси, отримані в результаті застосування інструментів фінансової та грошової політики.

Умови динамічної моделі IS-LM збігаються з умовами статичної моделі.

Як інструмент фінансової політики розглядаються державні видатки G, зміна яких впливає на рівень випуску через механізм витратного мультиплікатора.

Як інструмент грошової політики виступає пропозиція грошей M S, зміна якої відображається на співвідношенні основних еле-

ментів попиту на гроші — для трансакційних операцій ( M paymentsD ) та як на актив ( M assetsD ) — і впливає на рівень ставки відсотка і.

104

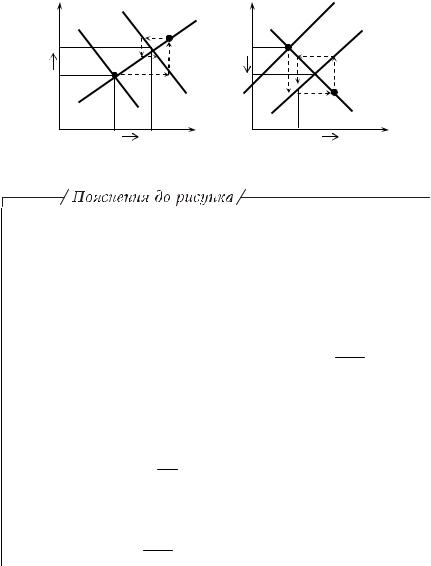
Послідовність змін макроекономічних параметрів — Y та і — під впливом фінансових та грошових інструментів зображена за логікою ітераційної (павутиноподібної) моделі на рис. 1.23.

X Графіки ілюструють те, що застосування інструментів фінансової та грошової політики порушує раніше досягнуту рівновагу і спричиняє рух у бік нової рівноваги (перехід від точки

E до E′ ).

X Перехід до нової рівноваги при отриманні економікою фінансового імпульсу (графік 1) охоплює п’ять кроків (ітерацій), що мають такий економічний зміст:

1)збільшення державних витрат приводить до мультиплікативного зростання випуску за рівнянням ∆Y = ∆G 1−1c′ ;

2)зростання випуску веде до збільшення трансакційного попиту на гроші ( ∆M paymentsD = k∆Y ), а для збереження відповідно-

сті M D = M S попит на гроші як на актив має зменшитись ( ∆M paymentsD = −∆M assetsD = h∆i ), відповідно, відсоткова ставка має

зрости в обсязі: ∆i = k ∆hY ;

3) збільшення ставки відсотка призводить до падіння інвестиційного попиту за рівнянням ∆I = −b∆i , а зменшення інвестицій, своєю чергою, викликає мультиплікативне скорочення

випуску: − ∆Y = −∆I 1−1c′ ;

105

4)скорочення випуску сприятиме зменшенню трансакційного попиту на гроші, а отже, збільшенню попиту на гроші як на актив з відповідним зменшенням ставки відсотка в обсязі:

−∆i = k −∆hY ;

5)зменшення ставки відсотка стимулюватиме інвестиційний попит ( ∆I = −b(−∆i) ), який спричинить зростання випуску в об-

сязі:

∆Y = ∆I 1−1c′ .

X Перехід до нової рівноваги при отриманні економікою грошового імпульсу (графік 2) охоплює п’ять кроків (ітерацій),

що мають такий економічний зміст:

1) збільшення пропозиції грошей M S порушує рівновагу грошового ринку, для відновлення якої передбачається зростання попиту на гроші як на актив з відповідним зниженням ставки відсотка:

∆M S = ∆M assetsD = −h∆i ;

2) зниження ставки відсотка приводить до збільшення інвестицій [ ∆I = −b(−∆i) ] та мультиплікативного зростання випуску:

∆Y = ∆I 1−1c′ ;

3) збільшення випуску викликає зростання трансакційного попиту на гроші (∆M paymentsD = k∆Y ) і відповідне зменшення попиту на гроші як на актив (∆M paymentsD = −∆M assetsD = h∆i) та зростання

∆Y

h;

4)збільшення ставки відсотка призводить до скорочення інвестицій ( ∆I = −b∆i ) і до мультиплікативного скорочення випуску:

−∆Y = −∆I 1−1c′ ;

5)зменшення випуску спричиняє зменшення трансакційного

попиту на гроші й коригувальне зростання попиту на гроші як на актив і зниження ставки відсотка:∆ =

− ∆i = k −∆hY .

106

Послідовність подій у разі порушення рівноваги внаслідок фінансовогоімпульсуможнавідобразитиувигляділогічноголанцюжка:

— ітерації 1, 2, 3:

G↑ → Y↑ →M paymentsD ↑ → M assetsD ↓ → i↑ → I↓ → Y↓;

— ітерації 4, 5:

Y↓ → M paymentsD ↓ → M assetsD ↑→ i↓ → I ↑→ Y↑.

Послідовність подій при порушенні рівноваги внаслідок грошового імпульсу можна подати у вигляді логічного ланцюжка:

— ітерації 1; 2; 3:

M S↑ → M assetsD ↑ → i↓ → I↑ → Y↑→ M paymentsD ↑ → M assetsD ↓ → i↑

— ітерації 4, 5:

i ↑→ I↓ → Y↓ → M paymentsD ↓→ M assetsD ↑ → i↓.

Динамізація статичної моделі IS-LM дає можливість пояснити два явища:

формування різних варіантів динамічної рівноваги;

ефективність фінансових та грошових імпульсів.

Варіантами динамічної рівноваги можуть бути:

• детермінована (визначена) стабільна рівновага — поступове

наближення параметрів системи до новогорівноважного стану;

•недетермінована (невизначена) стабільна рівновага — ста-

більне (з незмінною амплітудою) коливання параметрів системи навколо нового рівноважного стану;

•недетермінована і нестабільна рівновага — наростаюча ам-

плітуда коливань і поступове віддалення параметрів системи від нового рівноважного стану.

Для оцінки ефективності фінансової та грошової політик у рамках динамізованої моделі IS-LM можуть бути використані графічний і аналітичний методи.

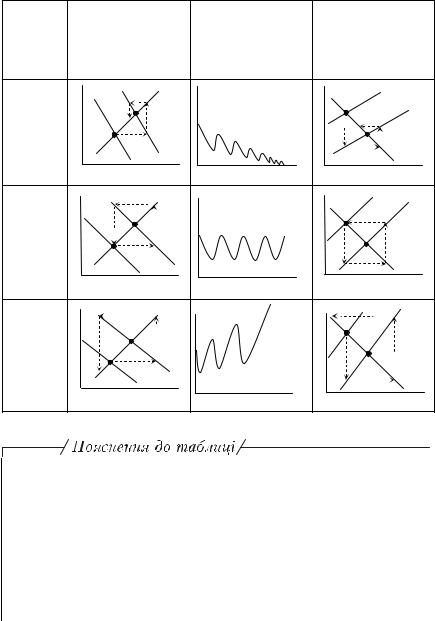
Умови та механізми формування різних типів рівноваги при застосуванні фінансових і грошових інструментів подані в табл. 1.8.

З графіків у табл. 1.8 випливає правило (умова) ефективності: якщо виходити з того, що після зовнішніх імпульсів економіка має досягти визначеної і стабільної рівноваги, то це стає можли-

вим лише за умови, що кут нахилу функції IS до горизонтальної осі є більшим, ніж кут нахилу LM.

107

X Таблиця дає можливість ілюструвати зв’язок між співвідношенням кутів нахилу функцій IS та LM, з одного боку, та типом рівноваги, яка формується після фінансових і грошових імпульсів, — з другого.

X За умови, що кут нахилу функції IS до горизонтальної осі є меншим, ніж кут нахилу LM, після фінансового та грошового імпульсів формується визначена і стабільна рівновага за логікою вже розглянутих нами ітерацій 1—5. Відбуватиметься рух точки E до точки нової рівноваги E′, або математично — досягатиметься нульове значення абсолютної різниці між E та E′: |∆EE′| = 0.

108

X Якщо нахили функцій IS та LM однакові, то рух до точки Е здійснюється з незмінною амплітудою коливань навколо нової рівноваги, хоча вона і не досягатиметься, а економіка набуває ознак стабільно невизначеної рівноваги. За визначенням П. Самуельсона, уцьомуразі спостерігається стабільність «другого порядку».

X При більшому нахилі функції IS порівняно з функцією LM після одержаних імпульсів економіка віддаляється від точки нової рівноваги з наростаючою амплітудою, а стан економіки характеризується як невизначена і нестабільна рівновага.

Аналітичний метод оцінки ефективності політик дає змогу сформулювати вимоги до кількісних співвідношень параметрів (коефіцієнтів), які визначають нахили ліній IS та LM. Логіка застосування аналітичного методу на прикладі стимулювальної фі-

нансової політики така:

Згідно з пунктами 1—3 пояснених нами ітерацій при застосуванні фінансової політики легко визначити співвідношення початкового приросту випуску ∆Y1 і наступного його зменшення ∆Y2:

1)∆Y = 1 −1c′ ∆G ;

2)∆i = kh ∆Y1 ;

3)∆I = − bkh ∆Y1 .

Тоді ∆Y2 = ∆I 1 −1c′ ∆Y2 = −1 −1c′ bkh ∆Y1 .

Співвідношення ∆Y1

∆Y2

на повному циклі руху точки тимчасової рівноваги:

α= ∆Y1 = h(1 − c′) .

∆Y2 bk

Якщо α > 1, це означає, що на кожному циклі чистий приріст випуску буде додатним. При цьому кожний новий цикл починатиметься з більшого значення Y, а прирости Y, навпаки, будуть зменшуватись. Це означає, що після застосування стимулювальної фінансової політики в економіці спостерігатимуться згасаючі коливання, у результаті яких досягатиметься нова детермінована рівновага за більшого рівня випуску. Отже, фінансова політика є

ефективною.

109

Якщо α < 1, це означає, що на кожному циклі чистий приріст випуску буде від’ємним, а коливання випуску будуть збільшуватись. У цьому разі економіка дедалі більше віддалятиметься від стану детермінованої рівноваги, а фінансова політика є неефек-

тивною.

Якщо α = 1, то чисті прирости випуску будуть нульовими, рівень випуску та ставка відсотка коливатимуться з постійною частотою й амплітудою навколо своїх рівноважних рівнів. Якщо економічні параметри перейдуть від стану детермінованої рівноваги до стану недетермінованої стабільної рівноваги, то фінансова політика не може бути визнана ефективною, навіть якщо коливання відбуватимуться навколо цільових рівнів випуску та ставки відсотка.

Логіка застосування аналітичного методу при оцінці ефектив-

ності стимулювальної грошової політики подібна до тієї, що за-

стосована до стимулювальної фінансової політики. Ефективність грошової політики буде оцінюватись абсолютним співвідношенням початкового приросту випуску і наступного його зменшення:

∆Y1 . За розрахунками, ефективність грошової політики визна-

∆Y2

чатиметься тим самим показником, що й ефективність фінансової політики:

α= ∆Y1 = h(1 − c′) .

∆Y2 bk

Отже, спільне для оцінки ефективності двох політик правило, виведене при використанні аналітичного методу, таке: фінансова та грошова політика ефективні лише за умови α > 1, а якщо α ≤ 1, жодна з політик не є ефективною.

Аналітичним методом може бути визначена і порівняльна ефективність політик. При цьому використовується підхід, реалізований у статичній моделі IS-LM, та враховується умова встановлення детермінованої стабільної рівноваги α > 1:

Фінансова політика з урахуванням ефекту витіснення буде максимально ефективною при

110