
Экзамен 2021 / Панков Пособие по ТВиМС часть 1
.pdfзаконе больших чисел). С помощью этого приближенного равенства мы можем
оценить число «пи» экспериментально. Т. к. |
r |
|
m |
, то |
r n |
. |
a |
n |
|
||||
|
|
|
am |
|||
В 1850 году математик Вольф 5000 раз бросал иглу и получил 3,1596. Лаззерини в 1901 году 3408 раз бросал иглу. Его оценка - 3,14159 . Гриджеман в 1960 году бросил иглу 2 раза и получил 3,143.
Схема испытаний Бернулли
Пусть у нас имеется случайный эксперимент ,A, .
1 , 2 , A P .
1 p,0 p 1, 2 1 p q.
Обозначим 1 через 1 и назовем успехом, а 2 через 0 и назовем неудачей
(неудачей).
Более сложный случайный эксперимент заключается в повторении этого
случайного эксперимента. |
|
|
|
раза): 2,A2, 2 |
|||||
Рассмотрим n 2 (повторяем 2 |
|||||||||
2 |
0,0 , 0,1 , 1,0 , 1,1 , |
A P 2 , |
|
|
|||||
2 |
0,0 0 0 q2 |
0 |
|
|
|
|
|
||
2 |
0,1 0 1 qp 0 |
|
|
|
|
|
|
||
|
q |
2 |
pq qp p |
2 |
1 |
||||
2 |
1,0 1 0 pq 0 |
|
|
|
|||||
|
|
|
|
|
|
||||
2 1,1 1 1 p |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2,A2, 2 -вероятностная (математическая) модель сложного случайного
эксперимента, состоящего в двух простых повторениях исходного эксперимента.
Повторим эксперимент n-раз:
n |
1... n : i 0,1 , |
где i - результат i-го повторения исходного |
||
эксперимента. |
|
|
|
|
... n , A |
n |
P( ), |
||
n |
|
|
n |
|
n раз
Рассмотрим элементарное событие ( 1... n) . Обозначим через m число
n
единиц в : m k .
k 1
n
Тогда пусть n( ) ( n) pmqn m .
k1
1)n( ) 0 для всех n
2)n( 1... n) 1
( 1... n )
Докажем последнее равенство:
|
P |
|
.. |
|
|
n |
|
|
P |
|
.. |
|
|
|
n |
|
|
|
n |
|
|||||||
n |
1 |
|
|
|
n |
1 |
|
|
|||||
1.. n |
|
|
|
|
|
m 0 |
|
1.. n : i m |
|
|
|
|
|
31

n
Cnm pmqn m p q n 1. m 0
Мы получили вероятностное пространство n,An,Pn -математическую
(вероятностную) модель случайного эксперимента, состоящего в n -кратном повторении исходного эксперимента.
Эту модель и называют схемой независимых испытаний Бернулли или
биноминальной схемой. |
|
|
|
|
|
|
|
|
Рассмотрим |
задачу: |
пусть проведено |
n испытаний |
по схеме |
Бернулли. |
|||
Буквой обозначим число успехов в n |
испытаний. Какова вероятность того, |
|||||||
что m? |
|
|
|
|
|
|
|
|
P m |
pmqn m Cnm pmqn m , |
где m |
|
. |
|
|
||
0,n |
|
|
||||||
1.. n : i m |
|
|
|
|
|
|
|
|
Равенство P m Cnm pmqn m называется формулой Бернулли. |
|
|||||||
Примеры: 1. |
Пусть |
100 раз бросают |
правильный |
тетраэдр, |
{1,2,3,4}, |
|||
P i 1 , где i 1,4. n
Пусть успех – выпадение грани «3», тогда неудача – выпадение граней «1», «2», «4».
p P 3 1 , 4
q P 1,2,4 P 1 P 2 P 4 1 p 3 . 4
Имеем схему Бернулли. Какова вероятность того, что «3» выпадет 15 раз?
|
1 |
15 |
3 |
85 |
385 |
|
||||
P m 15 C15 |
|
C15 |
. |
|||||||
|
|
|
|
|
|
|
||||
100 |
4 |
4 |
100 |
2 |
200 |
|
||||
|
|
|
|
|
|
|
|
|||
2. По каналу связи передают 500 знаков. вероятность искажения одного знака равно 0,01. Какова вероятность того, что в телеграмме 7 искаженных знаков?
P 7 C7 |
|
|
1 |
7 |
x |
|
|
99 |
493 |
C7 |
|
99493 |
. |
|
|
|
|
|
|
|
|
1000 |
|||||
500 |
100 |
|
100 |
500 |
|
||||||||
|
|
|
|
|
|
|
10 |
|
|||||
Какова вероятность того, что число успехов заключено в фиксированных пределах? По формуле Бернулли
|
|
|
m2 |
|
|
|
|
|
m2 |
|
|
P m1 m2 P k Cnk pkqn k . |
|||||||||
|
|
|
k m1 |
|
|
|
|
|
k m1 |
|
Теперь |
обозначим |
C |
m Cm pmqn m P m . Пусть n – фиксировано. |
|||||||
|
|
|
|
|
n |
|
|
|
n |
|
Рассмотрим отношение вероятностей |
||||||||||
|
C m 1 |
|
Cm 1pm 1qn m 1 |
|
Cm 1 |
|
p |
|||
|
n |
|
n |
|
|
|
n |
|
|
|
|
C m |
Cm pmqn m |
|
Cm |
|
|||||
|
|
|
|
|
|
q |
||||
|
n |
|
n |
|
|
|
n |
|
|
|
n!
m 1 ! n m 1 ! p n m p . n! qq m 1
m! n m !
32

Нужно найти, когда предыдущая вероятность больше последующей, т.е.
когда |
Cn m 1 |
|
n m |
|
p |
1. |
Cn m |
m 1 |
|
||||
|
|
|
q |
|||
Легко провести преобразования:
n m p m 1 q 0,
np mp mq q 0, np m p q q 0,
np m q 0.
Если np q m, то следующая вероятность больше предыдущей.
Если np q не целое число, тогда наиболее вероятным числом успехов является число m np q 1. Если np q - целое, то максимума Cn m достигает при m np q и при m np q 1
Пример: Пусть мы 100 раз бросаем несимметричный тетраэдр.
1,2,3,4 ,
P 1 1 , P 2 2 , P 3 3 , P 4 4 . 10 10 10 10
Пусть выпадение грани «3» - успех. Какое количество раз она выпадет с наибольшей вероятностью?
p |
3 |
, q |
7 |
, np q 100 |
|
2 |
|
|
7 |
30 0,7 29,3 . |
10 |
10 |
|
10 |
|
10 |
|
||||
Cn m |
максимально при m np q 1 30. |
|||||||||
Полиномиальная схема
Имеется случайный эксперимент ,A, .
1, 2,.. r ,
A P ,
r
k pk 0, k 1,r , pk 1.
k 1
Пусть эксперимент независимо повторяется n – раз. Получаем вероятностное пространство n,An, n , где
n .. n i1.. in ,
An P n ,
n
i1.. in ik .
k 1
n
1) i1.. in ik 0,
k 1
2) i1.. in 1.
1.. n
Докажем последнее равенство. Для этого рассмотрим множество из векторовi1.. in таких, что событие 1 повторяется в них m1 раз; 2 m2 и так далее.
33

Таких цепочек (их число мы считали в полиномиальной теореме) |
n! |
|
. |
||||||||||||
m1!m2 !..m2 ! |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i1 .. in |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1.. n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||
1.. n |
|
|
m1,m2 ,..,mr 0 |
|
1 |
повторяется m1 раз |
|
|
|
|
|
|
|||
|
|
|
r |
|
повторяется m раз |
|
|
|
|
|
|||||
|
|
|
mi n |
2 |
... |
2 |
|
|
|
|
|
|
|
||
|
|
|
i 1 |
|
повторяется mr |
|
|
|
|
|
|
|
|||
|
|
|
|
r |
раз |
|
|
|
|
|
|
||||
|
|
|
n! |
|
p1m1 p2m2 ..prmr 1. |
|
|
|
|
|
|
||||
m1 |
|
|
|
|
|
|
|
|
|||||||
|
mi 0 |
!m2 !..mr ! |
|
|
|
|
|
|
|
|
|
||||
|
m1 .. mr n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее равенство следует из полиномиальной теоремы. |
n,An, n |
|
|||||||||||||
Мы |
получили новое вероятностное |
|
пространство |
- |
|||||||||||
математическую (вероятностностную) модель n – кратного повторения случайного эксперимента с r исходами в каждом при неизменных условиях. Эта модель называется полиномиальной схемой. При r 2 мы получаем биномиальную схему.
Пусть 1 - число исходов 1 в случайном исходе полиномиальной схемы2 - число исходов 2 в случайном исходе полиномиальной схемы
…
r - число исходов r в случайном исходе полиномиальной схемы
1.. r - полиномиальный вектор.
r |
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что k |
n. |
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
Какова вероятность того, что 1 |
k1; 2 |
k2;...; r |
kr , если ki n? |
||||||||
|
|
n! |
|
|
|
|
|
|
|
i 1 |
|
1 k1; 2 k2;...; r kr |
|
|
k |
|
k |
k |
r . |
|
|||
|
|
|
p 1 |
p |
2 ..p |
|
|||||
k !k |
!..k |
! |
|
||||||||
|
1 2 |
|
r |
|
|
|
|
|
|
|
|
Данное равенство носит название полиномиальной формулы, частный ее случай – формула Бернулли:
1 k1, 2 k2 n k1
|
n! |
|
pk1 1 p n k1 |
Ck1 |
pk1 qn k1 . |
|
k1! n k1 ! |
||||||
|
|
n |
|
|||
|
|
|
|
|||
Пример: 24 раза бросаем игральную кость. Какова вероятность того, что каждая сторона выпадет по 4 раза?
1,2,..6 , |
|
r=6, |
p i |
1 |
|
|
для всех i |
|
, |
|||||||||||||||||
|
|
|
1,6 |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4; |
|
4;...; |
|
4 |
24! |
|
1 4 |
1 4 |
.. |
1 4 |
|
|||||||||||||
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
|
4!4!..4! |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
6 |
|
|
6 |
|
|||||||
|
|
|
|
24! 1 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4! |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
34

Теоремы Муавра – Лапласа и Пуассона
Рассмотрим биноминальную схему с вероятностью успеха p , где 0 p 1. Пусть m - событие, заключающееся в том, что при n испытаниях успех появился ровно m раз.
Если n и m небольшие, то вычислить P m по формуле Бернулли довольно
просто. Но при больших n вычисление будет крайне трудоемким. Поэтому в таких случаях следует для оценки использовать приближенные
формулы, к которым и относят формулы, следующие из предельных теорем Муавра-Лапласа и Пуассона.
Сформулируем без доказательства полезную формулу.
Утверждение (формула Стерлинга - без доказательства). Для любого
|
|
|
|
n |
|
n |
|
|
|
n |
|
|
|
n |
|
|
|
|
n |
||||
|
|
|
|
|
|
||||||
натурального n верно, что n! |
2 n |
|
|
e12n , где 0 n 1, или n! |
2 n |
|
. |
||||
|
|
||||||||||
|
|
e |
|
|
|
|
e |
||||
Теперь сформулируем первую предельную теорему.
Теорема (Локальная теорема Муавра-Лапласа). Дана биноминальная схема с вероятностью успеха р такой, что 0 p 1. Пусть m m n - целое число,
зависящее от n, такое, что последовательность |
x n |
m n |
np |
ограниченна |
||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
npq |
||
(т. е. существует |
c 0: |
|
|
x n |
|
|
c для всех |
n ). |
Рассмотрим событие m , |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
заключающееся в том, что произошло ровно m исходов. |
||||||||||||||||||||||||||||||||||||||
Тогда при n стремящемся к бесконечности |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
P m Cnm pmqn m |
|
|
1 |
|
|
|
|
|
|
1 |
|
e |
x2 n |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
npq |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
Доказательство. По формуле Стирлинга |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
P m |
|
|
|
n! |
pmqn m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
m! n m ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
n n |
n |
|
|
n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 n |
|
|
|
p |
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n m |
|
|
|
|
|
|
|||||||||||||
|
|
|
m |
|
|
|
|
|
|
|
n |
|
m |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 m |
|
2 |
n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
np m |
|
n |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 n |
m |
|
|
|
|||||||||||
|
|
|
|
|
m |
m |
n m |
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n |
n |
|
|
|
|
||||
n m
q .
Из определения последовательности x n :
n m |
|
nq x |
n |
npq |
|
|
|
|
|
1 |
q, так как |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
||||
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||||||
|
m np x n |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||
|
npq |
|
|
|
|
|
|
|
|
|
|
||||||||||
m |
|
np x n |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
npq |
p |
|
|
|
|
p, так как |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n |
|
|
n |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||
35

n m n np x n 
 npq nq x n
npq nq x n 
 npq .
npq .
Используя формулу Тейлора
ln 1 x x x2 O x3 ,
2
получаем
np m |
|
|
nq n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
n m ln |
n m |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
exp mln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
np |
|
|
|
nq |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
m n |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
exp |
|
|
np x(n) |
|
npq |
|
ln |
|
1 |
|
|
|
|
|
|
|
n |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
nq x(n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
nqp)ln 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
|
|
|
|
|
|
|
1 x2 n |
|
|
q |
|
|
|
|
|
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
exp |
|
np x(n) |
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/2 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n p 2 n |
|
|
|
p |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x n |
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 n p |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
nq x(n nqp) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3/2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
q 2 n q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
exp p n x n |
|
|
|
|
|
|
x2 |
n q x2 n q |
n 1/2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
q n x n |
|
|
|
|
|
|
|
|
|
|
x |
|
|
n p x |
|
n p n |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x2 n (p q) n 1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
exp |
|
|
|
n x n p |
|
|
|
q |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
q |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
exp 1 x2 n .
2
Отсюда получаем, что при n , и x n c:
|
|
|
|
|
|
|
1 |
|
|
|
|
|
e |
x2 |
n |
1 |
1 |
|
e |
x2 |
n |
|||||||||||
|
P m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
npq |
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
m |
n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема доказана. |
||
Получается, что оценка вероятности |
|
P m |
верна при |
|
x n |
|
c, т. е. при |
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
a |
m n |
np |
b, где a |
и b |
– некоторые константы. |
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда из локальной теоремы (вероятность в точке) мы можем получить интегральную теорему (вероятность промежутка). Для этого рассмотрим
m 1 np x n 
 npq ,
npq ,
x n m 1 np , npq
x n x n x n 1 , npq
36
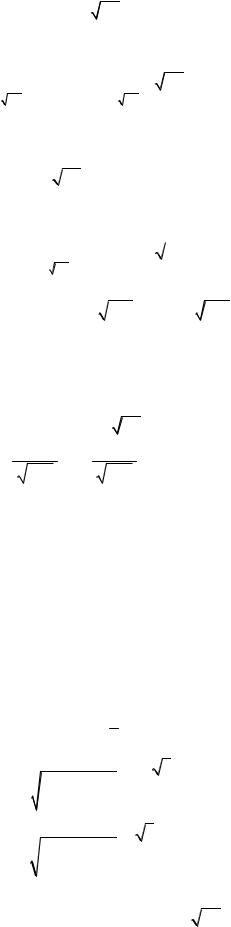
тогда P m |
|
1 |
|
|
|
e |
x2 n |
x n 1 n 1/2 |
|||||||||||||
|
|
|
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
Сумма вероятностей |
|
|
|
|
x2 n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
P m |
|
|
|
|
|
|
e |
|
x n 1 n 1/2 |
|||||||||||
|
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
m:a |
m |
np |
b |
|
|
m:a |
m |
np |
b |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
npq |
|
|
|
|
|
|
|
|
npq |
|
|
|
|
|
|
||||
с точностью до множителя 1 n 1/2 является интегральной суммой для
b |
1 |
|
e |
x2 |
|||
интеграла |
|
|
|
dx. |
|||
|
|
2 |
|||||
|
|
|
|||||
2 |
|||||||
а |
|
|
|
|
|||
В силу определения определенного интеграла получаем
|
|
|
|
|
|
|
|
|
b |
|
2 |
|
|
|
||||||
lim |
|
|
P |
|
|
1 |
e |
x |
dx, |
|||||||||||
|
m |
|
2 |
|||||||||||||||||
|
|
|
||||||||||||||||||
n |
|
|
|
|
|
|
|
2 |
||||||||||||
|
m:a |
m np |
b |
|
|
|
а |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где A m B ; |
a |
|
np |
|
; |
b |
В |
np |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
npq |
|
|
|
|
npq |
||||||||
Таким образом мы доказали следующую теорему:
Теорема (интегральная теорема Муавра – Лапласа). В условиях предыдущей теоремы для любых натуральных и таких, что верно
|
B |
|
|
|
|
1 |
b |
|
|
x2 |
|
lim |
|
P |
|
|
|
|
e |
|
dx, |
||
m |
|
2 |
|||||||||
|
|
|
|||||||||
n |
|
|
|
2 |
|
|
|
|
|||
|
m A |
|
|
|
|
а |
|
|
|
|
|
где a np ,b np . npq npq
Еще раз подчеркнем, что интегральная и локальная теоремы Муавра-Лапласа предназначаются для приближенного вычисления биноминальных вероятностей, либо их сумм.
Пример. Правильная кость подбрасывается 12000 раз. Какова вероятность того, что выпадение числа «6» будет лежать в пределах от 1800 до 2100?
2100 |
|
|
|
k |
|
|
12000 k |
|
1 |
|
5 |
|
|||||
k |
||||||||
Искомая вероятность равна C12000 |
|
|
|
|
|
|
|
|
6 |
10 |
|||||||
k 1800 |
|
|
|
|
||||
Понятно, что вычисление этой суммы крайне трудоёмко. Если мы воспользуемся интегральной теоремой Муавра-Лапласа, то найдем, что интересующая нас вероятность приближенно вычисляется следующим образом:
n 12000, p 1 , 18000, 2100;
6
a |
|
1800 2000 |
|
|
|
|
2 |
|
4,898, |
|
|
|
||||||||||||||||||
|
|
|
|
|
6 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
12000 |
1 |
|
|
5 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b |
|
2100 2000 |
|
|
|
|
|
|
|
2,449, |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
12000 |
1 |
|
5 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2100 |
|
|
|
|
1 |
k |
5 |
|
12000 k |
1 |
2,449 |
|
x2 |
|||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
C12000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e 2 dx . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
10 |
|
|
2 4,898 |
||||||||||||||||||||||||
k 1800 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
37

|
|
|
|
|
|
|
|
|
1 |
|
x |
y2 |
||
Рассмотрим функцию x |
|
|
e |
|
dy , тогда |
|||||||||
|
|
2 |
||||||||||||
|
|
|
||||||||||||
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2100 |
|
|
|
k |
12000 k |
|
|
|
|
|
|
|
||
1 |
|
5 |
|
|
|
|
|
|
|
|
||||
k |
|
|
|
|
|
|
|
|||||||
C12000 |
|
|
|
|
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
|
|||||||||
k 1800 |
|
|
10 |
|
|
|
|
|
|
|
|
|||
2,449 4,998 0,992.
Численные значения x берутся из таблицы значений этой функции
(функции распределения стандартного нормального закона, с которой мы познакомимся позднее более подробно).
Процесс приближенного вычисления одной функции с помощью другой можно назвать аппроксимацией. Аппроксимация суммы биноминальных вероятностей с помощью функции x , то есть теоремы Муавра-Лапласа, при
значениях р, близких к нулю или единице, может быть «плохой» (то есть дающей большую погрешность) даже при больших значениях n. При этих, «малых» значениях р «хорошую» аппроксимацию для нашей суммы дает так называемая теорема Пуассона.
Рассмотрим биноминальную схему испытаний при n испытаниях. Будем
менять n так, чтобы |
n , |
|
|
а |
|
|
вероятность успеха p p n |
будем считать |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
функцией параметра n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Теорема (Пуассона). |
|
|
|
|
|
|
|
Пусть в биномиальной схеме при n |
стремящемся |
||||||||||||||||||||||||||||||||||||||||||||||||||||
к бесконечности |
|
|
|
|
p p n |
|
0; при этом n p n , где 0. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||||||||
Тогда для любого фиксированного m 0,1,2,... |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
limP |
|
|
|
|
limCm pm |
|
n |
|
|
1 p |
|
n |
|
n m |
|
m |
e . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
m |
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m! |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Доказательство. Очевидно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
P m Cnm pm n 1 p n n m |
|
n n 1 .. n m 1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
p n |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m! |
|
|
|
|
|
|
|
|
|
|||||||||||
|
n |
1 p n |
n |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
nm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
m |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
np n n |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
... 1 |
|
|
|
|
|
|
|
|
np n |
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||||||
m! |
|
n |
|
n |
|
|
|
n |
|
1 p n |
m |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Устремим n |
|
|
к бесконечности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
m 1 |
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
lim |
1 |
|
1 |
|
|
|
... 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
lim |
np |
|
n |
|
|
m |
|
|
|
|
lim |
np |
|
n |
|
|
m |
m , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
n p n |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
lim 1 p n |
lim |
|
|
|
|
|
|
|
|
|
p n |
|
|
e |
, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
1 p n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n 1 p n m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
38

Из полученных равенств следует, что
limCnm pm n 1 p n n m |
|
1 |
m e . |
|
|||
n |
|
m! |
|
|
|
|
Теорема доказана. |
Теорему Пуассона |
используют для приближенного вычисления |
||
биноминальных вероятностей, когда значения р малы, а число испытаний n
велико. Обычно, если p n 10, |
то для аппроксимации биноминальных |
||||||
вероятностей |
используют |
теорему |
Пуассона, а |
если p n 10, то |
теоремы |
||
Муавра – Лапласа. |
|
|
|
|
|||
Обратим |
внимание, |
что в |
предыдущем |
рассмотренном |
примере |
||
p n 12000 |
1 |
|
2000 10. |
|
|
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
|
|
|
Пример. Пусть на Московский рынок завезли партию цыплят из 10000 тушек. Известно, что их завезли из области, где 0,05 процентов поголовья больны птичьим гриппом. Найти вероятность того, что в поставке было не более одной опасной для здоровья тушки.
Имеем
n 10000 104 , p 0,05 5 10 4 ,
100
np 5 10.
Следовательно, нужно использовать теорему Пуассона.
P 1 P 0 P 1 50 e 5 51 e 5 0! 1!
6e 5 0,04.
39
Тема №5 Случайные величины и случайные векторы
Рассмотрим произвольное вероятностное пространство
понятие, призванное формально определить величины, подлежащие «измерению» в случайных экспериментах.
Определение. Случайной величиной называется функция
заданная на пространстве элементарных событий , принимающая значения ви удовлетворяющая условию, что для любого вещественного х множество
является событием, т.е.
w : w x A.
Пример: Пусть случайный эксперимент состоит в двукратном
подбрасывании монеты: 00,10,01,11 . |
|
|
|
|
|
||||
Определим случайную величину |
с помощью таблицы |
||||||||
|
|
00 |
|
10 |
|
01 |
|
11 |
|
Здесь число |
|
0 |
|
1 |
|
1 |
|
2 |
|
означает |
число |
гербов в элементарном исходе. |
|||||||
Другим простейшим |
примером |
случайной |
величиной является |
||||||
индикатор наступления некоторого |
события А A: I A , где |
||||||||
1, .
0,
Определение. Функцией распределения случайной величины называется функция F x : , равная
F x P : x P x .
Теорема (о свойствах функции распределения). Для любой случайной величины верно:
1.0 F x 1 для любых x ;
2.F x - неубывающая функция на ;
3. |
lim F x 0, |
lim F x 1; |
|
|
|
|
|
|
|
|
||||||
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||
4. |
F |
x0 непрерывна слева в любой точке x0 |
, т. е. |
|
|
|
||||||||||
lim |
F x F x |
или |
|
|
|
|
|
|
|
|
||||||
x x 0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0: x x0 ,x0 |
|
F x F x0 |
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
Свойство 1 следует из определения F x |
и свойств вероятностной меры. |
||||||||||||||
2. |
Пункт |
2 |
|
следует |
из |
того, |
что |
если |
x1 x2 , |
то |
||||||
: x1 : x2 и, |
следовательно, P x1 P x2 . |
|
||||||||||||||
3. |
Так как F x |
- |
неубывающая |
и ограниченная функция, то существуют |
||||||||||||
пределы: lim F |
x b, |
и lim F x а. Требуется доказать, что b 1 |
и а 0. |
|
||||||||||||
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
||
40
