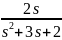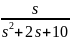лаб 2

Министерство науки и высшего образования Российской Федерации Калужский филиал федерального государственного бюджетного образовательного учреждения высшего образования «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)» (КФ МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ	ИУК «Информатика и управление»____________
КАФЕДРА	ИУК3 «Системы автоматического управления и электротехника»_______

лабораторная работа №2

«Преобразование Лапласа. Нахождение оригинала функции по её изображению»

ДИСЦИПЛИНА: «Основы управления в технических системах»

Выполнил: студент гр. ИУК1-51Б	_______________ (_Прудников А.Ф.) (Подпись) (Ф.И.О.)
	_______________ (_Ломакин С.А.__) (Подпись) (Ф.И.О.)
Проверил:	_______________ (Корнюшин Ю.П._)

(Подпись) (Ф.И.О.)

Дата сдачи (защиты):

Результаты сдачи (защиты):

- Балльная оценка:

- Оценка:

Калуга, 2021 г.

Цель лабораторной работы: формирование практических навыков по использованию преобразования Лапласа для исследования систем управления.

Задача лабораторной работы: освоение свойств преобразования Лапласа, способов вычисления оригинала функции по её изображению, а также применение MATLAB к вычислению оригиналов функций по их изображениям. Закрепить полученные знаний на практике.

Практическая часть

Вариант, №	Задание 1(2)	Задание 3(4)
1

Задание 1

p=[1 3 2]

b=[2 0]

r=roots(p)

r1=r(1); r2=r(2)

dp=polyder(p)

A1=polyval(dp,r1)

A2=polyval(dp,r2)

B1= polyval(b, r1)

C1=B1./A1

B2= polyval(b, r2)

C2=B2./A2

t=[0:0.01:5];

x=C1.*exp(r1.*t)+C2.*exp(r2.*t);

plot(t,x),grid on, xlabel('Time(sec)'), ylabel('x(t)')

Рис. 1. – График функции, построенный с использованием оператора plot(t,x).

Изображению 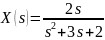соответствует оригинал .

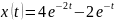Проверим правильность преобразований. Для этого воспользуемся предельными теоремами.

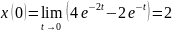
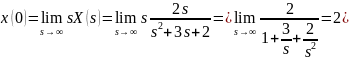
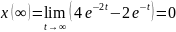
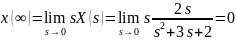
Задание 2

p=[1 3 2]

b=[2 0]

r=roots(p)

r1=r(1); r2=r(2)

dp=polyder(p)

A1=polyval(dp,r1)

A2=polyval(dp,r2)

B1= polyval(b, r1)

C1=B1./A1

B2= polyval(b, r2)

C2=B2./A2

C3=C1./(r1)

C4=C2./(r2)

B0=polyval(b,0)

A0=polyval(p,0)

C0=B0./A0

x1=C0+C3.*exp(r1.*t)+C4.*exp(r2.*t);

t=[0:0.01:5];

plot(t,x1), grid on, xlabel('Time(sec)'), ylabel('x1(t)')

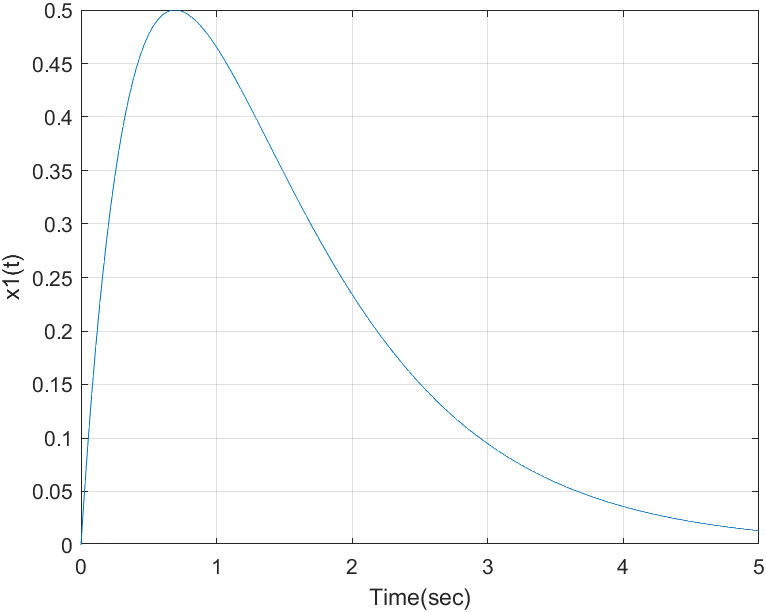
Рис. 2. – График функции, построенный с использованием оператора plot(t,x).

Изображению 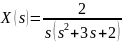соответствует оригинал .

Проверим правильность преобразований. Для этого воспользуемся предельными теоремами:

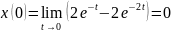
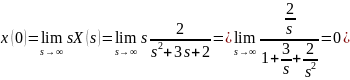
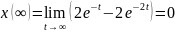
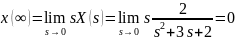
Задание 3

p=[1 2 10]

b=[1 0];

r=roots(p)

r1=r(1)

dp=polyder(p)

A1=polyval(dp, r1)

B1=polyval(b, r1)

C1=B1./A1

t=[0:0.01:5];

Для формирования функции коэффициент С1 домножаем на

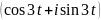
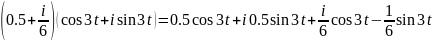и оставляем вещественную часть

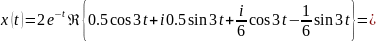
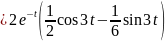
x= exp(-t).*cos(3.*t)-1.6667.*exp(-t).*sin(3.*t);

plot(t,x), grid on, xlabel('Time(sec)'), ylabel('x(t)')

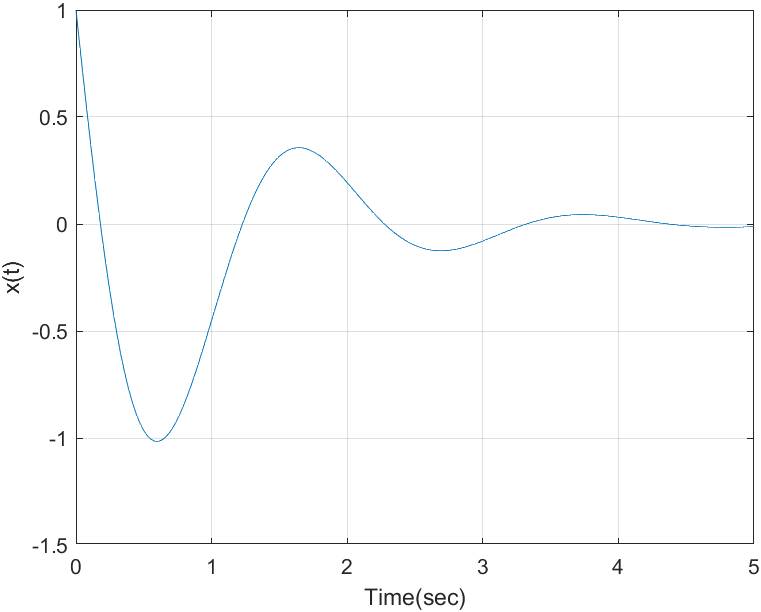
Рис. 3. – График функции, построенный с использованием оператора plot(t,x).

Изображению 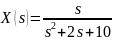соответствует оригинал .

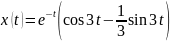Проверим правильность преобразований. Для этого воспользуемся предельными теоремами:

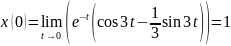
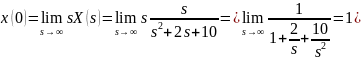
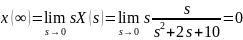
Задание 4

p=[1 2 10]

b=[1 0];

r=roots(p)

r1=r(1)

dp=polyder(p)

A1=polyval(dp, r1)

B1=polyval(b, r1)

C1=B1./A1

C3=C1./r1

A0=polyval(p,0)

B0=polyval(b,0)

C0=B0./A0

t=[0:0.01:5];

Для формирования функции коэффициент С3 домножаем на

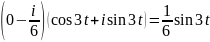
Далее оставляем вещественную часть и домножаем на 2.

x=0.33.*exp(-t).*sin(3.*t);

plot(t,x), grid on, xlabel('Time(sec)'), ylabel('x(t)')

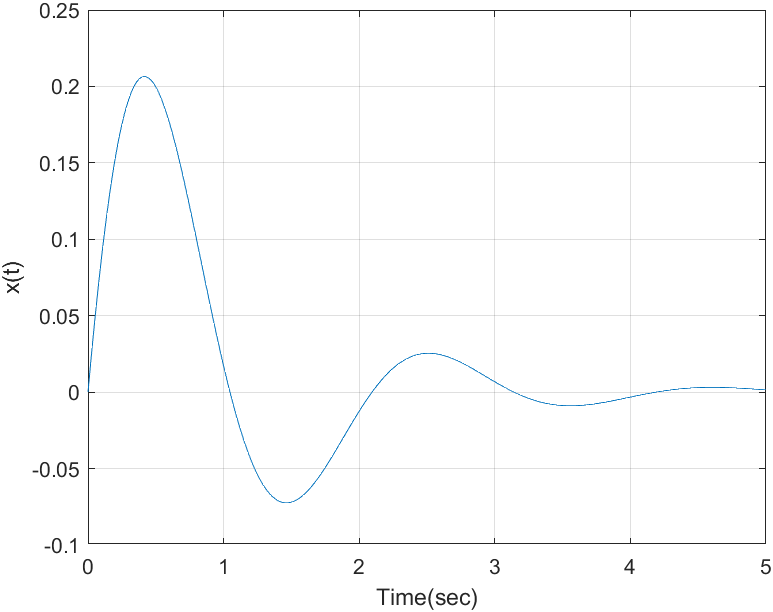
Рис. 4. – График функции, построенный с использованием оператора plot(t,x).

Изображению 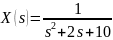соответствует оригинал

.

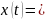
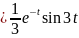Проверим правильность преобразований. Для этого воспользуемся предельными теоремами:

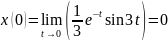
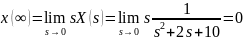
Вывод: сформировали практические навыки по использованию преобразования Лапласа для исследования систем управления, а также освоили свойства преобразования Лапласа, способы вычисления оригинала функции по её изображению, а также применение MATLAB к вычислению оригиналов функций по их изображениям. Закрепили полученные знания на практике.