15. Тепловое излучение. Функция Планка. Квантовая гипотеза.

Функция Планка. Для получения согласующегося с опытом выраже- ния испускательной способности абсолютно черного тела М. Планку при- шлось отказаться от принятого в классической физике положения, согласно которому энергия любой системы может меняться непрерывно. Он выдвинул

гипотезу, в соответствии с которой атомы излучают энергию не непрерыв- но, а определенными порциями – квантами, причем энергия кванта пропор- циональна частоте колебания:

где h = 6,625×10^–34 Дж×с – постоянная Планка.

Основываясь на этой гипотезе, М. Планк в 1900 г. получил выраже- ние универсальной функции Кирхгофа

Эта формула полностью описывает распределение энергии в спектре излучения абсолютно черного тела во всем интервале частот и температур, полученное экспериментально.

Учитывая связь между испускательной способностью, зависящей со- ответственно от переменных ν и λ, получаем

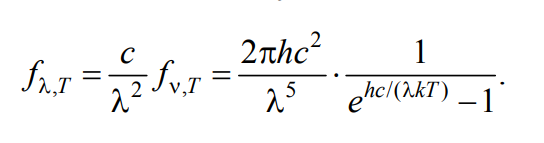
На рис. 2.1 приведены графики зависимости функций Кирхгофа от длины волны для разных температур.

f_λ,Т, отн. ед. 0,8

0,6

0,4

0,2

^{0 λ3 λ2 λ1 1000} λ, нм

16. Тепловое излучение. Закон смещения Вина. Закон Стефана-Больцмана.

Тепловое излучение - это электромагнитное излучение, которое возникает за счет энергии вращательного и колебательного движения атомов и молекул в составе вещества. Тепловое излучение характерно для всех тел, которые имеют температуру, превышающую температуру абсолютного нуля.

Тепловое излучение характеризуется сплошным спектром, положение максимума которого зависит от температуры. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких — преимущественно длинные (инфракрасные).

Основными количественными характеристиками теплового излучения являются: - энергетическая светимость - это количество энергии электромагнитного излучения во всем диапазоне длин волн теплового излучения, которое излучается телом во всех направлениях с единицы площади поверхности за единицу времени: R = E/(S·t), [Дж/(м²с)] = [Вт/м²] Энергетическая светимость зависит от природы тела, температуры тела, состояния поверхности тела и длины волны излучения. - спектральная плотность энергетической светимости - энергетическая светимость тела для данных длин волн (λ + dλ) при данной температуре (T + dT):  R_λ,T  = f(λ, T). Энергетическая светимость тела в пределах каких-то длин волн вычисляется интегрированием R_λ,T  = f(λ, T) для T = const:

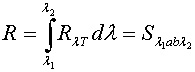
Согласно закону Стефана — Больцмана, т. е. энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры; — постоянная Стефана— Больцмана, ее экспериментальное значение равно 5,67 • 10^-8 Вт/(м^2 * К^1 ).

Закон Стефана—Больцмана, определяя зависимость Re от температуры, не дает ответа относительно спектрального состава излучения черного тела.

Закон смещения Вина устанавливает зависимость длины волны, на которой спектральная плотность потока излучения чёрного тела достигает своего максимума, от температуры чёрного тела.

При повышении температуры максимум универсальной функции Кирхгофа

смещается в сторону более коротких волн и притом так, что выполняется соотношение

maxT =b .

Экспериментально установлено значение постоянной Вина b =2.898 *10^-3 м * К. Закон Вина объясняет переход излучения в длинноволновую часть спектра при остывании (переход белого каления в красное при остывании металла). Связь спектра излучения и температуры излучателя позволяют определить цветовую температуру. Цветовая температура тела - температура абсолютно черного тела, излучающее в том же цветовом тоне, что и излучающее тело. Понятие о цветовой температуре применяется в астрофизике, фотометрии, колориметрии и оптической пирометрии.

Кривые зависимостей спектральной плотности излучения абсолютно чёрных тел с различными температурами от длины волны.

Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких длин волн.

17. Фотоэффект. Вольт-амперная характеристика фотоэффекта.

Фотоэффект — явление взаимодействия света или любого другого электромагнитного излучения с веществом, при котором энергия фотонов передаётся электронам вещества. В конденсированных (твёрдых и жидких) веществах выделяют внешний (поглощение фотонов сопровождается вылетом электронов за пределы тела) и внутренний (электроны, оставаясь в теле, изменяют в нём своё энергетическое состояние) фотоэффект. Фотоэффект в газах состоит в ионизации атомов или молекул под действием излучения.

Внешним фотоэффектом называется испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.

Внутренним фотоэффектом называется явление возрастания электропроводности и уменьшения сопротивления, вызванное облучением. Он объясняется перераспределением электронов по энергетическим состояниям в твёрдых и жидких полупроводниках и диэлектриках, происходящее под действием излучений, проявляется в изменении концентрации носителей зарядов в среде и приводит к возникновению фотопроводимости или вентильного фотоэффекта.

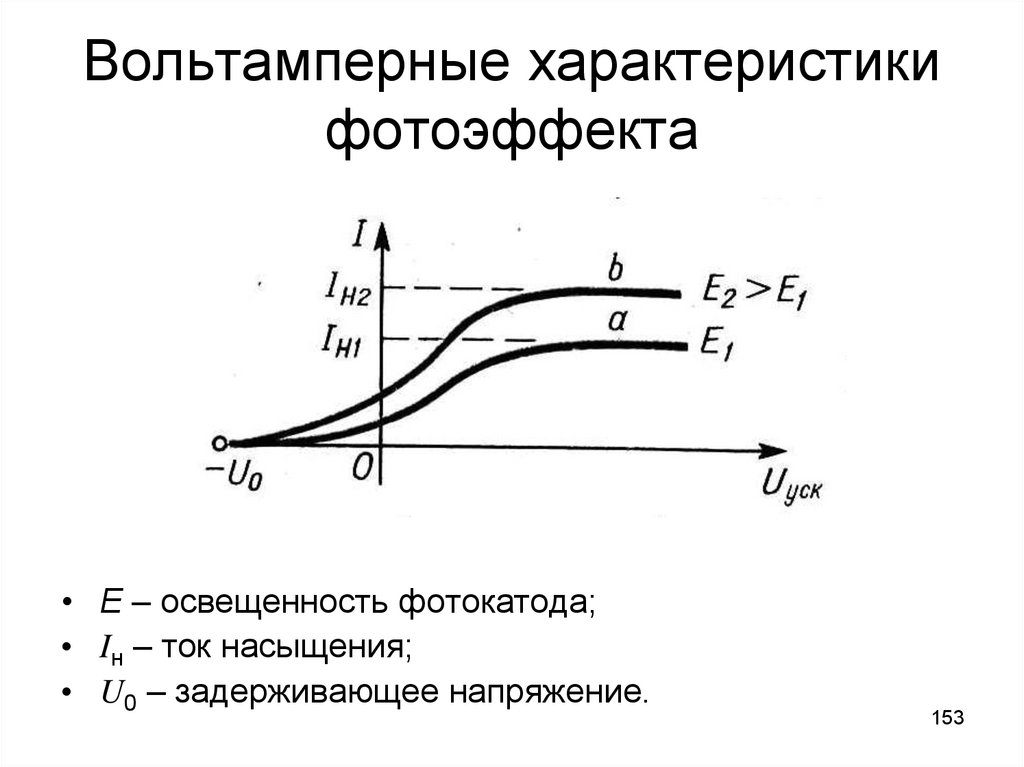
Вольт-ампер­ной характеристики фотоэффекта — зависимости фототока I, образуемого потоком электронов, испускаемых катодом под действием света, от напряжения U между электродами. Максимальное значение тока I_нас —фототок насы­щения — определяется таким значением U, при котором все электроны, испускаемые катодом, достигают анода: I_нас=ne ,где n — число электронов, испускаемых катодом в 1 с.

Из вольт-амперной характеристики следует, что при U=0 фототок не исчезает. Следовательно, электроны, выбитые светом из катода, обладают некоторой начальной скоростью v, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Для того чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение U₀. При U=U₀ ни один из электронов, даже обладающий при вылете из катода максимальной скоростью v_max, не может преодолеть задерживающего поля и достигнуть анода. Следовательно,  измерив задерживающее напряжение U₀, можно определить максимальные значе­ния скорости и кинетической энергии фотоэлектронов.

18. Законы внешнего фотоэффекта. Формула Эйнштейна для фотоэффекта.

Суть фотоэффекта заключается в том, что при освещении металлической поверхности пучком света из металла при определенных условиях вылетают электроны. Фотоэффект был открыт Г. Герцем

Фотоэффект можно наблюдать на установке, изображенной на рис. 2.2. В откачанной вакуумной трубке имеется кварцевое окошко Kв для освещения одного из электродов (катода К) пучком света. На электроды подается напряжение от батареи ε. Его величина U изменяется с помощью реостата П и измеряется вольтметром V. При освещении катода из него вылетают электроны, которые начинают двигаться к аноду А, если он находится под более высоким напряжением, чем катод. Достигшие анода электроны создают в цепи ток, называемый фототоком. Фототок регистрируется микроамперметром mА.

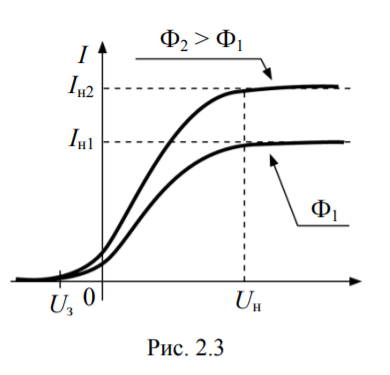
На рис. 2.3 показана зависимость силы фототока I от напряжения U между анодом и катодом для разной освещенности катодов Ф1 и Ф2. Как видно из рисунка, при напряжении Uн, которое называется напряжением насыщения, сила фототока достигает максимального значения (Iн1 или Iн2). Это максимальное значение фототока Iн называется фототоком насыщения. При U ≥ Uн все электроны, покинувшие катод под действием света, достигают анода.

Наличие фототока при изменении полярности между К и А (область значений U < 0 на рис. 2.2) объясняется тем, что вырванные из катода электроны имеют кинетическую энергию, достаточную для прохождения пространства между катодом и анодом в задерживающем электрическом поле. Электроны обладают максимальной кинетической энергией измерить которую можно, подав на анод задерживающее напряжение Uз, полностью тормозящее электроны. При Uз фототок I прекращается. Из закона сохранения энергии следует, что где m – масса электрона; vmax – его максимальная скорость/

Законы внешнего фотоэффекта.

1. Максимальная энергия фотоэлектронов зависит от частоты (длины волны) падающего на катод света и не зависит от освещенности катода (интенсивности света).

2. Число электронов, которые вырываются светом из катода в единицу времени, и сила фототока насыщения прямо пропорциональны освещенности катода.

3. Для каждого вещества существует такая наименьшая частота ν0 (или наибольшая длина волны λ0 = с/ν0), при которой еще возможен внешний фотоэффект. Значения этих величин называются красной границей фотоэффекта.

Кванты света. Уравнение Эйнштейна.

Все закономерности фотоэффекта находят объяснение, если предположить, что свет представляет собой поток корпускул – фотонов, или квантов света, распространяющихся в вакууме со скоростью света и обладающих энергией Е = hν.

Фотоны – кванты электромагнитного поля. Эти частицы обладают энергией и импульсом. Монохроматическую электромагнитную волну можно представить как поток фотонов. Импульс фотона p имеет то же направление, что и волновой вектор волны k. Импульс фотона, его энергия, частота и длина волны связаны соотношениями

При внешнем фотоэффекте каждый поглощенный металлом фотон передает всю свою энергию hν электрону проводимости металла. Для выхода из металла электрон должен совершить некоторую работу, называемую работой выхода Авых, оставшаяся часть энергии фотона переходит в кинетическую энергию электрона. Уравнение внешнего фотоэффекта Эйнштейна есть закон сохранения энергии при фотоэффекте:

19. Комптоновское рассеяние и законы сохранения.

Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ-излучения) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны этого излучения. Данный эффект был открыт в 1923 г. американским физиком А. Комптоном. В нем наиболее отчетливо проявляются корпускулярные свойства света. Оказалось, что в составе рассеянного излучения наряду с излучением первоначальной длины волны λ1 наблюдается также излучение с длиной волны λ2 > λ1. Этот эффект не находит объяснения в рамках волновой теории, согласно которой длина волны рассеянного излучения должна совпадать с длиной волны падающего: под действием электрического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.

Эффект Комптона объясняется на основе квантовых представлений о природе света: излучение имеет корпускулярную природу, т. е. представляет собой поток фотонов, и эффект Комптона есть результат упругого столкновения фотонов со свободными электронами вещества. В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в согласии с законами сохранения.

Пусть на покоящийся электрон падает световая волна частотой ν1. Эта волна эквивалентна потоку частиц (фотонов) с энергией E1 = hν1 и импульсом p1=E1/c. В результате электромагнитного взаимодействия с электроном фотон изменяет свои энергию и импульс, так что они становятся равными E2 = hν2 и p2=E2/c и рассеивается под некоторым углом θ по отношению к первоначальному направлению движения. Одновременно при упругом столкновении с фотоном электрон получает импульс и начинает двигаться под углом к первоначальному направлению со скоростью v

Используя законы сохранения импульса и энергии для процесса столкновения, находим изменение ∆λ длины волны фотона, которое оказывается равным

20. Строение атома. Опыт Резерфорда по рассеянию альфа-частиц. Планетарная модель атома Резерфорда.

Согласно планетарной модели атома, большая часть его массы сконцентрирована в крошечном (по сравнению с размерами всего атома) ядре. Электроны двигаются вокруг ядра, путешествуя с невероятной скоростью, но большая часть объема атомов является при этом пустым пространством. Размер ядра настолько мал, что его диаметр в 100 000 раз меньше, чем у атома. Диаметр ядра была оценен Резерфордом как 10^-13 см, в отличие от размера атома – 10^-8 см. За пределами ядра электроны вращаются вокруг него с высокими скоростями, в результате чего возникают центробежные силы, уравновешивающие электростатические силы притяжения между протонами и электронами.

Опыт

Резерфорд решил нацелить луч альфа-частиц на лист очень тонкой золотой фольги. Он выбрал золото, потому что из него можно получать листы толщиной всего 0,00004 см. За листом золотой фольги он поставил экран, который светился, когда альфа-частицы ударяли в него. Его использовали для обнаружения альфа-частиц после их прохождения через фольгу. Небольшая прорезь в экране позволяла лучу альфа-частиц достичь фольги после выхода из источника. Часть из них должна пройти сквозь фольгу и продолжать двигаться в том же направлении, другая их часть должна отскакивать от фольги и отражаться под острыми углами.

Исходя из модели атома Томсона, Резерфорд предполагал, что сплошные области положительного заряда, заполняющие весь объем золотых атомов, будут отклонять или сгибать траектории всех альфа-частиц, когда они проходят через фольгу. Однако подавляющее большинство альфа-частиц прошло прямо через золотую фольгу. Лишь немногие из них отклоняются от прямого пути, как и предполагалось вначале.

Крошечный процент частиц возвращался от фольги. Резерфорд понял, что эти отклонения были результатом прямого столкновения между альфа-частицами и положительно заряженными компонентами атома.

Исходя из ничтожного процента отразившихся от фольги альфа-частиц, можно сделать вывод, что весь положительный заряд и практически вся масса атома сосредоточены в одной маленькой области, а в остальной части атома в основном находится пустое пространство. Резерфорд назвал площадь концентрированного положительного заряда ядром. Он предсказал и вскоре обнаружил, что оно содержит положительно заряженные частицы, которые он назвал протонами.

21. Постулаты Бора. Модель Бора для атома водорода.

Первый постулат Бора (постулат стационарных состояний).

В атоме существуют стационарные (не изменяющиеся со временем) состояния – орбиты электронов, движение по которым не сопровождается излучением электромагнитных волн. Эти орбиты выделяются среди других тем, что на них электрон в атоме водорода имеет строго определенные дискретные (квантовые) значения момента импульса

Здесь n = 1, 2, 3, …

Соответственно энергия электрона на каждой из этих орбит имеет определенное значение Еn. Другие значения энергии невозможны.

Второй постулат Бора (правило частот).

При переходе электрона с одной стационарной орбиты на другую атом излучает (или поглощает) один фотон с энергией

где Еn и Em – энергии стационарных состояний атома.

Переход атома из состояния с большей энергией в состояние с меньшей энергией (Еm < Еn), т. е. переход электрона с более удаленной от ядра орбиты на более близкую, сопровождается излучением фотона. Переход атома в состояние с большей энергией (Еm > Еn), т. е. переход электрона на более удаленную от ядра орбиту, характеризуется поглощением фотона. Совокупность дискретных частот ν= (En – Em)/h квантовых переходов и определяет линейчатый спектр атома.

Боровская теория атома водорода.

Сформулированные Бором постулаты позволили вычислить радиусы разрешенных орбит и энергию электрона на них для атома водорода (Z = 1). Решая систему из двух уравнений, первое - движение электрона по круговой орбите радиусом r, а второе – первый постулат Бора,

получаем радиусы стационарных орбит электрона

Радиус первой орбиты атома водорода (r1 = a0 = 0,528·10–10 м) называется боровским радиусом.

Полная энергия электрона в атоме водорода есть сумма его кинетической и потенциальной энергии:

где – постоянная Ридберга; hR = 13,6 эВ.

Из формулы энергии электрона в атоме следует, что энергия состояния атома зависит от значения n.

n - главным квантовым числом. Энергетическое состояние с n = 1 называется основным состоянием, состояния с n > 1 – возбужденными.

Согласно второму постулату Бора переход атома водорода (Z = 1) из возбужденного стационарного состояния n в стационарное (возбужденное или основное) состояние m с меньшей энергией сопровождается испусканием кванта с частотой

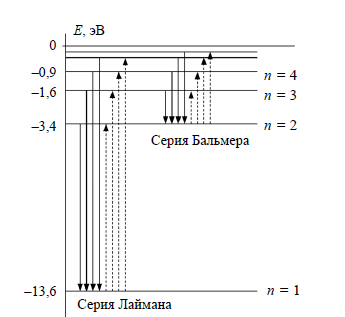
Эта формула совпадает с обобщенной формулой Бальмера и описывает все известные спектральные линии атома водорода (рис. 3.2, сплошные стрелки, направленные вниз, соответствуют излучению, штриховые – поглощению).

В основном состоянии (n = 1) электрон имеет наименьшее значение полной энергии Е1 = –hR = –13,6 эВ и наименьшее значение радиуса орбиты a0 = 0,528·10–10 м.

К серьезным недостаткам теории Бора следует отнести невозможность объяснить интенсивность спектральных линий и описать спектры других атомов кроме атома водорода, в том числе и атома гелия

радиус боровской орбиты rn = a0n2 в квантовой механике имеет смысл расстояния, на котором с наибольшей вероятностью может быть обнаружен электрон в состоянии c главным квантовым числом n.

22. Линейчатый спектр атома водорода. Формула Бальмера.

Линейчатый спектр атома водорода. Спектры излучения разреженных газов (т. е. индивидуальных атомов) имеют линейчатую структуру, состоящую из отдельных спектральных линий. Самым простым и наиболее изученным является спектр атома водорода – самого простого атома, состоящего из ядра и одного электрона.

И. Бальмер подобрал эмпирическую формулу (обобщенная формула Бальмера ), описывающую все известные в то время спектральные линии атома водорода в видимой области спектра: