
- •Теоретические основы электротехники
- •Теоремы Остроградского – Гаусса и Стокса
- •Используя выражение для электрического тока через некоторую поверхность S , ограниченную контуром l
- •Электростатическое поле
- •Определение электростатического поля
- •Потенциальность электростатического поля
- •Связь между потенциалом и напряженностью электрического поля
- •Проводя кривую « l » по разным направлениям, получим: 1. Проходя через точку
- •Направление вдоль линии напряженности перпендикулярно поверхности равного
- •Основная задача электростатики
- •Определение потенциала по заданному распределению заряда
- •Определение потенциала по заданному распределению зарядов
- •Определение потенциала по заданному распределению зарядов
- •Способы задания граничных условий в электростатических задачах
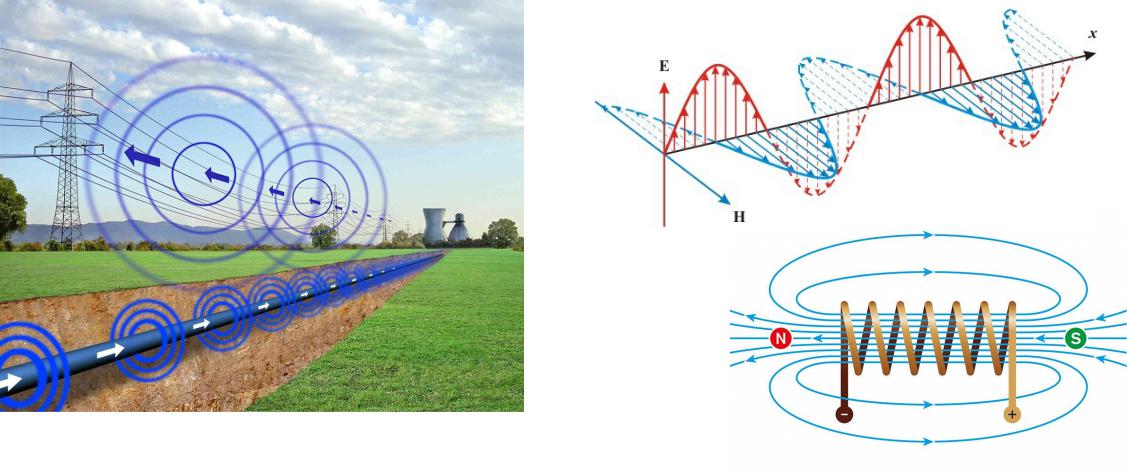
Теоретические основы электротехники
Теория электромагнитного поля
ВШВЭ, проф. Л. И. Сахно 2020
1
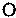
Теоремы Остроградского – Гаусса и Стокса
Теорема Остроградского – Гаусса позволяет преобразовать объемный интеграл в поверхностный, а теорема Стокса – поверхностный интеграл в линейный для произвольных функций, непрерывных вместе со своими первыми производными в исследуемых областях.
Запишем выражение для электрического заряда в некоторой области V, ограниченной замкнутой поверхностью S, и применим постулат Максвелла к левой и правой части этого уравнения:
q dV |
|
|
Dds div DdV |
||
V |
S |
V |
Теорема Остроградского – Гаусса:Интеграл от дивергенции вектора D по некоторому объему равен интегралу от вектора D по замкнутой поверхности, ограничивающей этот объем.
16

Используя выражение для электрического тока через некоторую поверхность S , ограниченную контуром l , и применив закон полного тока к обеим частям этого уравнения, получим:
|
|
|
|
i Jds |
|
||
|
Hdl rot Hds |
||
S |
l |
S |
|
Теорема Стокса: Интеграл от ротора вектора H по некоторой поверхности равен интегралу от вектора H по замкнутому контуру, ограничивающему эту поверхность
3
Электростатическое поле
Определение электростатического поля
Электростатическое поле создается неподвижными (по отношению к наблюдателю) электрическими зарядами. В таком поле отсутствуют электрические токи (J=0), а, следовательно, (при отсутствии намагниченных тел) и магнитное поле (H=0; B=0).
Из полной системы уравнений электромагнитного поля для электростатического поля получаем:
. |
|
B |
|
div D |
D E |
|
|
||||
|
rot E |
t |
0 |
|
|
В реальных устройствах объемные заряды в диэлектрике не могут находиться в покое, т.е. появляются электрические токи, что нарушат статичность поля. Поэтому во многих случаях второе уравнение имеет нулевую правую часть:
div D 0
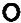
Потенциальность электростатического поля
Векторное поле , ротор которого равен нулю , называется безвихревым или
потенциальным
|
|
|
rot Eds Edl 0 |
- из теоремы Стокса |
|
|
|
|
S |
l |
|
Это соотношение определяет независимость интеграла между фиксированными точками от пути интегрирования
p |
|
- электрический потенциал |
b |
|
|
U a U b Edl |
|||
U а Edl |
|
|||
а |
|
|
a |
|
P - точка нулевого потенциала

Связь между потенциалом и напряженностью электрического поля
la
lp
|
E |
P |
|
l p |
l p |
|
U |
Edl E cos dl |
|||
|
|
||||
|
|
|
l |
l |
|
a |
dl |
|
U |
E cos |
|
|
|
|
l |
||
O 
Скорость изменения потенциала вдоль некоторого направления равна проекции вектора напряженности электрического поля на это направление со знаком минус.

Проводя кривую « l » по разным направлениям, получим: 1. Проходя через точку «a» в направлении осей координат:
U |
Ex |
U |
E y |
U |
E z |
x |
|
y |
|
z |
|
2. Проходя через точку «a» по линии l1 перпендикулярно вектору напряженности |
||||
электрического поля и вдоль него по линииl2 , получим: |
||||
U |
E cos 900 |
0 |
|
U E cos 00 E |
l1 |
l1 |
E |
|
l2 |
|
l2 |
Поверхности, перпендикулярные силовым линиям, |
||
|
|
|
называются равнопотенциальными |
|
|
a |
|
|
(эквипотенциальными). Это направление |
|
|
|
обозначают через «a» |
|
U |
U |
0 |
l |
a |
|
1 |
|
|
Направление вдоль линии напряженности перпендикулярно поверхности равного
потенциала. Часто это направление обозначают через «n», имея в виду нормаль к равнопотенциальной поверхности, тогда последнее соотношение можно записать иначе:
U |
|
U |
E |
l |
|
n |
|
2 |
|
|
|
U
Производная n ведет себя как вектор, имеет составляющие, определяемые направляющими косинусами, и называется градиентом потенциала.
U |
|
gradU E |
|
|
|
||||
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
U |
U |
||||
E gradU U |
x |
i |
y |
j |
|
z |
k |
||
|
|
|
|
|
|
|
|||
|
Уравнения Пуассона и Лапласа |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем уравнения электростатического поля, выразив векторные величины |
||||||||
|
через потенциал: |
|
|
|
|
|
|
|
|
|
div D |
div( E ) |
|
|
div ( grad U ) |
||||
|
Если const |
div gradU |
|
|
|||||
|
|
|
|
||||||
|
|
- уравнение Пуассона в инвариантной форме |
|||||||
|
|
|
|
|
|
|
|
||
|
div gradU 2 2U2 2U2 |
2U2 |
|
|
|
U - уравнение Пуассона в декартовой системе |
|||
|
|
|
|||||||
|
x |
y |
z |
|
|
|
координат |
||
|
|
|
|
|
|
|
|
|
|
|
div gradU 2U U 0 |
- уравнение Лапласа |
|||||||
- оператор Лапласа
