
Динамика точки и системы / Теоретическая механика
.pdf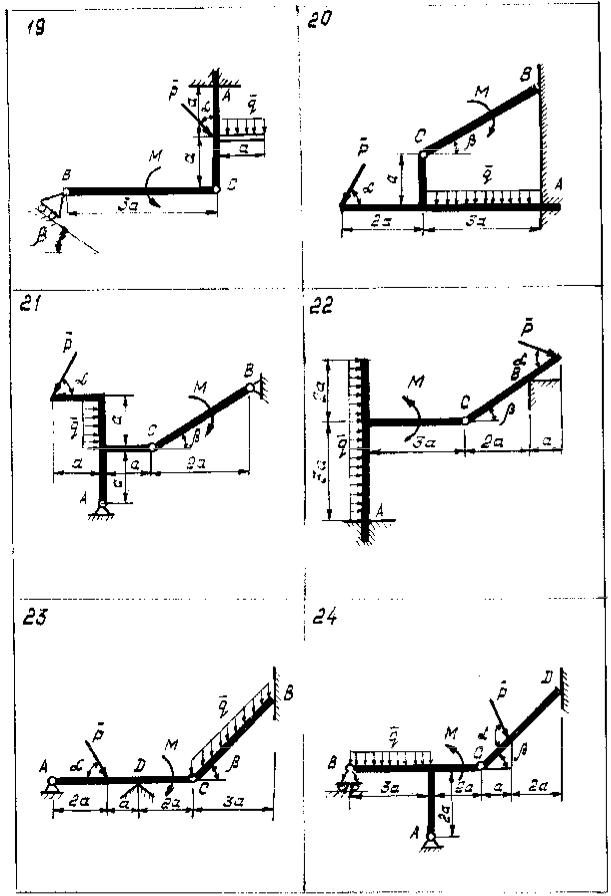
81
Рис. 2.4

82
Рис. 2.5
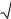
83 |
|
|
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ |
|
|
Дано: схема конструкции (рис. 2.6а); |
P = 8 кН; |
M = 20 кНм; |
q = 2 кН/м ; a = 1 м; α = 60о; β = 30о. Определить реакции опор A и B и давление в промежуточном шарнире C.
РЕШЕНИЕ
Данная конструкция состоит из двух тел, сочлененных шарниром C. Задачу можно решить двумя способами.
Первый способ. Мысленно освобождаемся от связей, наложенных на каждое из тел, заменяя их на соответствующие реакции. Рассматриваем системы уравновешивающихся сил, приложенных к каждому телу в отдельности.
На первое тело (рис. 2.6б) действуют: сила P , пара сил с моментом M, реакция опоры A и давление балки CD в точке C. Реакция жесткой за-
делки A представляется силами X A , YA и парой сил с моментом MА, а давление балки CD - составляющими XC и YC . Указанные силы расположены
на плоскости произвольным образом, поэтому составляем три уравнения равновесия:
åFKx = 0 |
; |
X A + XC - P ×cosα = 0 |
; |
(1) |
||||||
K |
|
|
|
|
|
|
|
|
|
|
åFKy = 0 |
; |
YA + YC - P ×sinα = 0 |
; |
(2) |
||||||
K |
|
|
|
|
|
|
|
|
|
|
åm0 (FK ) = 0 ; |
X A ×OA + M A + YC ×OC - M + P ×OK = 0 ; |
(3) |
||||||||
K |
OA = 2 × a = 2м , |
OC = 1,5 |
× a =1,5м , |
|
||||||
где |
|
|||||||||
|
|
|
|
|
= 0,87 |
|
|
|
||
|
OK = a ×sinα =1× |
3 |
м . |
|
|
|||||
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
На второе тело (рис. 2.6в) действуют: распределенные силы интенсивности q , реакция опоры B и давление первого тела в точке C. Равно-
мерно распределенные силы заменяем их равнодействующей Q , прило-
женной в середине участка CD и направленной по вертикали вниз. Ее модуль определяется по формуле:
Q = q ∙ CD = 2 ∙ 3,5 = 7 кН.
Реакция NB опоры B перпендикулярна к балке CD, а давление первого тела представляется составляющими XC′ и YC′ . Согласно аксиоме о равенстве действия и противодействия
84
|
|
Рис. 2.6 |
′ |
и |
′ |
XC = X C |
XC −↓ XC , |
|
YC′ = YC |
и |
YC′ −↓ YC . |

85
Уравнения равновесия сил, приложенных к балке CD имеют вид:
åFKx = 0 |
; |
|
′ |
|
|
β = 0 |
; |
|
|
|
|
(4) |
||||||
- XC - NB ×sin |
|
|
|
|
||||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åFKy = 0 |
; |
- YC′ + NB × cos β - Q = 0 |
; |
(5) |
||||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åmC (FK ) = 0 ; |
NB ×CB - Q ×CF = 0 |
; |
|
|
|
|
(6) |
|||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CF = CD ×cos β = |
3,5 |
|
|
|
|
|
|
|
|||||||||
где CB = a =1 м, |
× |
|
3 |
=1,52 |
м. |
|||||||||||||
|
|
2 |
|
|||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||||
Уравнения равновесия (1)-(6) образуют полную систему уравнений, |
||||||||||||||||||
откуда определяются все шесть неизвестных величин: XА, YА, MА, XС, YС, |
||||||||||||||||||
NB. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из уравнения (6) находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
NB = Q × CF |
= 7 × |
1,52 |
=10,64 |
|
кН. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
|
CB |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из уравнения (5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
YC¢ = NB ×cos β - Q =10,64× |
|
|
3 |
|
- 7 = 2,21 кН. |
|
||||||||||||
2 |
|
|
||||||||||||||||
Из уравнения (4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
¢ |
|
|
|
|
= -5,32 |
|
кН. |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
XC = -NB sin β = -10,64× |
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отрицательный знак указывает, что в действительности сила XC′ (соответственно и XC ) будет направлена в сторону противоположную принятой. Истинные направления сил XC и YC , представляющих собой состав-
ляющие давления RC балки CD на первое тело конструкции, показаны на
рис. 2.6г.
Модуль RC и угол определяются по формулам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= X |
2 + Y 2 = |
(5,32)2 + (2,21)2 |
= 5,76 кН, |
||||||||||||||||||
|
C |
|
|
C |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
||||
γ = arctg |
|
|
|
YC |
|
|
|
= arctg0,4154 = 22 |
o |
|
¢ |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
34 . |
|
|||||||||||||
|
|
|
XC |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
Далее из уравнения (1) находим |
|
|
|
|
||||||||||||||||||
X A = P ×cosα - XC = 8× 1 + 5,32 = 9,32 |
кН. |
|||||||||||||||||||||
Из уравнения (2) |
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
= 8× |
|
|
|
- 2,21 = 4,72 |
|
||||||||||||||
Y |
A |
= P ×sinα -Y |
3 |
кН. |
||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

86
Из уравнения (3)
M A = -X A ×OA - YC ×OC + M - P ×OK =
= -9,32× 2 - 2,21×1,5 + 20 - 8× 0,87 = -8,92 кН×м.
Отрицательный знак указывает, что направление вращения пары в опоре А в действительности противоположно выбранному.
Второй способ. Рассматриваем систему уравновешивающихся сил, приложенных ко всей конструкции (рис. 2.6а). На конструкцию действуют:
сила P , пара сил с моментом M, равнодействующая Q распределенных сил и реакции опор A и B ( X A ,YA ,M A , NB ). При рассмотрении всей конструк-
ции в целом давления в шарнире C ( XC ,YC и XC′ ,YC′ ) не рассматриваются. Уравнениями равновесия для указанной системы сил будут:
åFKx = 0 |
; |
X A - P × cosα - NB ×sin β = 0 |
; |
|
(7) |
|||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åFKy = 0 |
; |
YA - P ×sinα + NB ×cos β - Q = 0 |
; |
(8) |
||||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
åmA (FK ) = 0 ; |
M A + P × h1 - M + NB × h2 - Q × h3 = 0 ; |
(9) |
||||||||||||||||
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где h = a ×sinα + 2×a ×cosα = |
|
|
|
+ 2× 1 =1,87 |
|
|
|
|
|
|||||||||
3 |
м, |
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||
1 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
+ 2× 1 = 3,30 |
|
||||||
h |
= a +1,5a ×cos β + 2a ×sin β =1+1,5× |
|
3 |
|
|
м, |
||||||||||||
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
h =1,5a +1,75a ×cos β = 1,5 +1,75× |
|
|
3 |
|
= 3,02 |
м. |
|
|||||||||||
|
|
|
|
|
||||||||||||||
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Далее следует рассматривать систему уравновешивающихся сил, приложенных к одному из тел конструкции, при этом целесообразно выбрать ту часть конструкции, на которую действует меньшее число сил. В данном случае рассматриваем систему сил, действующих на балку CD, условия равновесия которой выражаются уравнениями (4) – (6).
Таким образом, для определения шести неизвестных величин будем иметь систему уравнений (4) – (9).
В заключении отметим, что уравнения (7) – (9) могут быть использованы для проверки результатов решения задачи первым способом, а уравнения (1) – (3) - вторым способом.
87
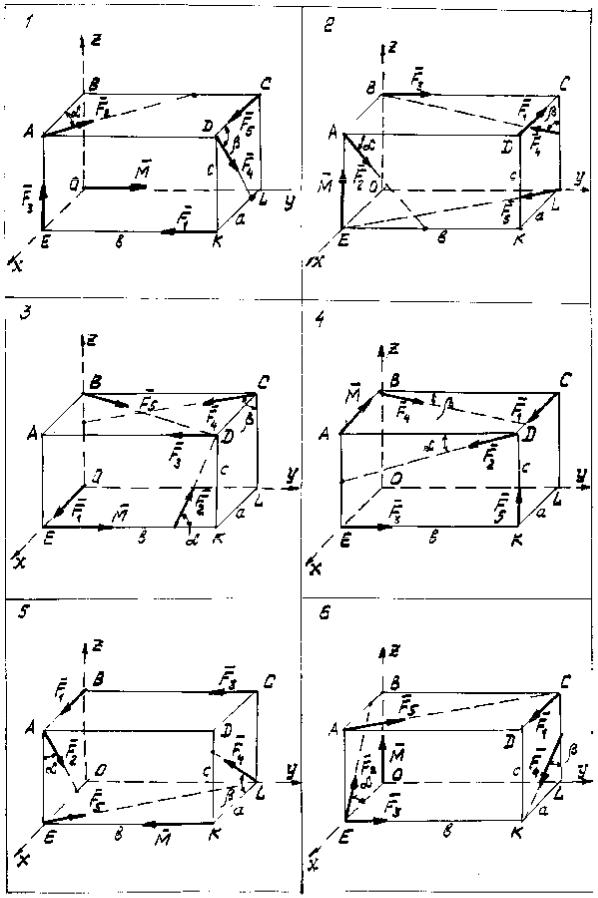
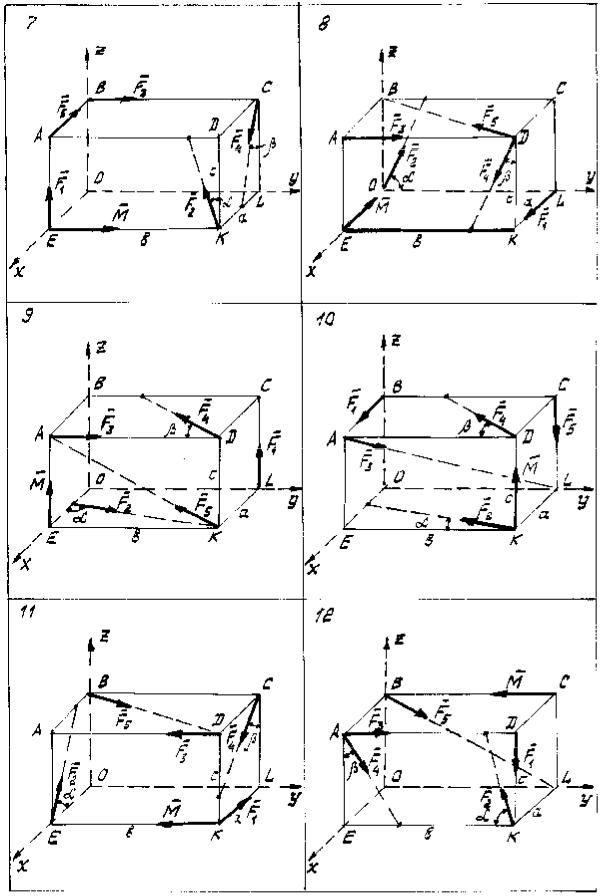
ЗАДАНИЕ С-3 Приведение пространственной системы сил к заданному центру.
Определить главный вектор R и главный момент M0 заданной сис-
темы сил относительно центра O. Схемы вариантов приведены на рис. 3.1– 3.5, необходимые данные - в таблице 3.
Таблица 3.
№№ |
a=OE, |
b=OL, |
c=OB, |
F1, |
F2, |
F3, |
F4, |
F5, |
α, |
β, |
М, |
п/п |
м |
м |
м |
H |
H |
H |
H |
H |
град |
град |
Нм |
1 |
15 |
20 |
15 |
9 |
14 |
12 |
14 |
15 |
60 |
30 |
10 |
2 |
30 |
40 |
30 |
12 |
18 |
16 |
18 |
20 |
75 |
15 |
20 |
3 |
45 |
60 |
45 |
15 |
22 |
20 |
22 |
25 |
30 |
60 |
30 |
4 |
60 |
80 |
60 |
18 |
26 |
24 |
26 |
30 |
15 |
75 |
40 |
5 |
15 |
20 |
15 |
21 |
30 |
28 |
30 |
35 |
60 |
30 |
10 |
6 |
30 |
40 |
30 |
24 |
34 |
32 |
34 |
40 |
75 |
15 |
20 |
7 |
45 |
60 |
45 |
27 |
38 |
36 |
38 |
45 |
30 |
60 |
30 |
8 |
60 |
80 |
60 |
30 |
42 |
40 |
42 |
50 |
15 |
75 |
40 |
9 |
15 |
20 |
15 |
33 |
46 |
44 |
46 |
55 |
60 |
30 |
10 |
10 |
30 |
40 |
30 |
36 |
50 |
48 |
50 |
60 |
75 |
15 |
20 |
11 |
45 |
60 |
45 |
12 |
54 |
16 |
54 |
20 |
30 |
60 |
30 |
12 |
60 |
80 |
60 |
15 |
58 |
20 |
58 |
25 |
15 |
75 |
40 |
13 |
15 |
20 |
15 |
18 |
17 |
24 |
17 |
30 |
60 |
30 |
10 |
14 |
30 |
40 |
30 |
21 |
19 |
28 |
19 |
35 |
75 |
15 |
20 |
15 |
45 |
60 |
45 |
24 |
21 |
32 |
21 |
40 |
30 |
60 |
30 |
16 |
60 |
80 |
60 |
27 |
23 |
36 |
23 |
45 |
15 |
75 |
40 |
17 |
15 |
20 |
15 |
30 |
25 |
40 |
25 |
50 |
60 |
30 |
10 |
18 |
30 |
40 |
30 |
33 |
27 |
44 |
27 |
55 |
75 |
15 |
20 |
19 |
45 |
60 |
45 |
36 |
29 |
48 |
29 |
60 |
30 |
60 |
30 |
20 |
60 |
80 |
60 |
9 |
31 |
12 |
31 |
15 |
15 |
75 |
40 |
21 |
15 |
20 |
15 |
9 |
14 |
12 |
14 |
15 |
60 |
30 |
10 |
22 |
30 |
40 |
30 |
12 |
18 |
16 |
18 |
20 |
75 |
15 |
20 |
23 |
45 |
60 |
45 |
15 |
22 |
20 |
22 |
25 |
30 |
60 |
30 |
24 |
60 |
80 |
60 |
18 |
26 |
24 |
26 |
30 |
15 |
75 |
40 |
25 |
15 |
20 |
15 |
21 |
30 |
28 |
30 |
35 |
60 |
30 |
10 |
26 |
30 |
40 |
30 |
24 |
34 |
32 |
34 |
40 |
75 |
15 |
20 |
27 |
45 |
60 |
45 |
27 |
38 |
36 |
38 |
45 |
30 |
60 |
30 |
28 |
60 |
80 |
60 |
30 |
42 |
40 |
42 |
50 |
15 |
75 |
40 |
29 |
15 |
20 |
15 |
33 |
45 |
44 |
46 |
55 |
60 |
30 |
10 |
30 |
30 |
40 |
30 |
36 |
50 |
48 |
50 |
60 |
75 |
15 |
20 |
88
Рис. 3.1
89
Рис. 3.2

90
Рис. 3.3
