
Динамика точки и системы / Теоретическая механика
.pdf
61
Примечание: силы инерции Фперин и Фкорин вполне реальны. Они появляются из-за наличия переносного движения. Их не следует путать с силами инерции F ин , рассматриваемыми ниже в разделе 3.1 «Принцип Даламбера», поскольку «даламберовы» силы инерции имеют фиктивный характер.
Векторное уравнение (1.15) спроецируем на оси относительной системы координат и получим три скалярных дифференциальных уравнения относительного движения материальной точки:
ì |
&& |
= Fx |
ин |
ин |
|
|
mx1 |
+ФперX |
+ ФкорX |
(1.16) |
|
ímy1 = Fy |
+Фпер |
+Фкор |
|||
ï |
&& |
|
ин |
ин |
|
ï |
|
|
Y |
Y |
|
&& |
= Fz |
ин |
ин |
|
|
îmz1 |
+ ФперZ |
+ ФкорZ |
|
||
Чтобы эти уравнения проинтегрировать, движение относительной системы координат должно быть известно.
2.Динамика системы материальных точек.
2.1 Основные понятия и определения.
Система материальных точек – это такая совокупность материальных точек, при которой точки системы каким-то образом связаны друг с другом и не могут перемещаться независимо друг от друга.
Внешние и внутренние силы. Любая сила, действующая на точку механической системы, обязательно является либо активной силой, либо реакцией связи. Однако всю совокупность сил, действующих на точки системы, можно еще разделить на два класса иначе: на внешние силы F e и внутренние силы F i (индексы e и i – от латинских слов externus – внешний и internus – внутренний). Внешними называют силы, действующие на точки системы со стороны точек и тел, не входящих в состав рассматриваемой системы. Внутренними называются силы, действующие между точками и телами рассматриваемой системы.
Это разделение зависит от того, какие материальные точки и тела включены для изучения в рассматриваемую механическую систему. Если расширить состав системы, включив в нее дополнительно точки и тела, то некоторые силы, которые для прежней системы были внешними, для расширенной системы могут стать внутренними.
Свойства внутренних сил. Если рассмотреть две произвольные точки механической системы, то, в соответствии с с третьим законом Нью-
62
тона (законом равенства действия и противодействия), они действуют друг на друга с силами, равными по ведичне и противоположными по направлению, следовательно геометрическая сумма этих сил равна нулю. Рассматривая таким образом попарно все точки механической системы, получаем следующие важные свойства внутренних сил:
∙геометрическая сумма всех внутренних сил системы равна нулю.
∙сумма моментов всех внутренних сил системы относительно произвольного центра равена нулю.
Массой системы M называется арифметическая сумма масс mk всех
точек и тел, образующих систему:
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
(2.1) |
|
|
|
|
|
|
|
|
M = åmk |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
Центром масс (центром инерции) механической системы называется |
|||||||||||||||||||
геометрическая точка C, радиус-вектор rc |
и координаты которой |
xc , yc , zc |
||||||||||||||||||
определяются формулами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n |
r |
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
åmk yk |
|
|
|
|
åmk xk |
|
|
|
|
åmk zk |
|
|
||
r |
åmk rk |
, |
|
|
|
, |
|
|
|
, |
|
|
|
, |
(2.2) |
|||||
r = |
k =1 |
|
y |
c |
= |
k =1 |
x |
c |
= |
k=1 |
|
z |
c |
= |
k =1 |
|
||||
|
|
|
|
|
|
|
||||||||||||||
c |
|
M |
|
|
|
M |
|
|
|
|
M |
|
|
|
M |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где rk |
- радиусы-векторы, а xk , yk , zk |
|
- координаты точек (или центров масс |
|||||||||||||||||
тел), образующих систему. Для твердого тела, находящегося в однородном поле тяжести, положения центра масс и центра тяжести совпадают, в других случаях - это разные геометрические точки.
Наряду с инерциальной системой отсчета в динамике часто рассматривают одновременно неинерциальную систему отсчета, движущуюся поступательно. Ее оси координат Cx*y*z* (оси Кёнuга) выбирают так, чтобы начало отсчета С постоянно совпадало с центром масс механической системы. В·соответствии с определением центр масс неподвижен в осях Кёнига и находится в начале координат.
Движение механической системы зависит не только от массы системы, но и от того, как эта масса распределена внутри системы. Охарактеризовать это распределение позволяют моменты инерции.
Моментом инерции системы относительно оси z называется ска-
лярная величина Iz равная сумме произведений масс m k |
всех точек сис- |
темы на квадраты их расстояний hk до оси z: |
|
n |
|
I z = åmk hk2 . |
(2.3) |
k =1 |
|
Если механической системой является твердое тело то, для нахождения Iz тело разбивают на n элементарных частиц и вычисляют предел
63
суммы (2.3), устремляя n к бесконечности, т.е. задачу сводят к интегрированию. В системе координат Oxyz можно воспользоваться формулой:
I z = òòòρ(x2 + y2 )dV , |
(2.4) |
V |
|
где ρ(х, у, z) - плотность, а V - объем, занимаемый телом.
Момент инерции однородного цилиндра (как частный случай - диска) массы т радиуса R относительно оси, совпадающей с осью цилиндра, подсчитывается по формуле:
I z |
= |
mR2 |
. |
(2.5) |
|
2 |
|
|
|
Момент инерции полого тонкостенного цилиндра (как частный слу- |
||||
чай - кольца) определяется как |
= mR2 . |
(2.6) |
||
I z |
||||
При вычислении моментов инерции относительно оси бывает удобно воспользоваться следующей теоремой:
Теорема Гюйгенса-Штейнера о моментах инерции относительно па-
раллельных осей, одна из которых проходит через центр масс: |
(2.7) |
I z = ICZ + Md 2 , |
где I z и ICZ - моменты инерции относительно параллельных осей z и CZ , причем ось Cz проходит через центр масс; d - расстояние между осями; M - масса системы (или твердого тела). Из теоремы следует, что ICZ < Iz .
Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Oz называется линейная
величина, ρин , определяемая равенством |
|
IZ = Mρин2 . |
(2.8) |
2.2 Теорема о движении центра масс
Теорема о движении центра масс системы: Центр масс механиче-
ской системы движется как материальная точка, масса которой равна массе всей системы, и к которой приложены все внешние силы, действующие на систему.
× r = ån r e .
M aC Fk
k =1
Спроецируем это тождество на инерциальные оси x, y, z, и получим:
2 |
xc |
n |
|
d |
2 |
yc |
n |
2 |
zc |
n |
||
M |
d |
= åFkeX , |
M |
|
= åFkeY , |
M |
d |
= åFkeZ , |
||||
dt |
2 |
dt |
2 |
dt |
2 |
|||||||
|
|
k =1 |
|
|
k =1 |
|
|
k =1 |
||||
(2.9)
(2.10)
Где xC , yC , zC - координаты центра масс С системы в осях Oxyz. Теорема доказана.

64
Закон сохранения движения центра масс механической системы:
если главный вектор внешних сил системы равен нулю, центр масс системы движется с постоянной скоростью:
если |
n |
r |
, |
то |
r |
åFke = 0 |
VC = const |
||||
|
k=1 |
|
|
|
|
Отметим, что в этом случае постоянным является вектор скорости, а не только его модуль, поэтому центр масс будет двигаться равномерно и прямолинейно (или покоиться, если VC (0)= 0 ).
Если проекция главного вектора внешних сил системы на какуюлибо ось равна нулю, то проекция скорости центра масс системы на эту ось остается постоянной. Например,
|
n |
|
|
|
|
если |
åFkeX |
= 0, |
то |
VCX |
= const |
|
k=1 |
|
|
|
|
|
и если |
VCX (0) = 0 , |
то |
xC |
= const |
2.3. Теорема об изменении количества движения
Количеством движения материальной точки массы т, движущей-
ся со скоростью V , называется вектор mV , равный произведению массы точки на ее скорость.
Количеством движения механической системы (главным векто-
ром количества движения системы) называется геометрическая сумма количеств движения всех точек системы:
r n |
r |
(2.11) |
Q = åmkVk . |
||
k =1
Можно доказать, что количество движения системы равно количеству движения воображаемой материальной точки, имеющей массу системы
и движущейся со скоростью центра масс системы: |
|
Q = M ×VC . |
(2.12) |
Импульс силы. Пусть к движущейся материальной точке приложена сила F (кроме нее к точке могут быть приложены и другие силы, но сейчас мы выделили только одну из них).
Элементарным импульсом силы F за элементарный промежуток времени
dt называется вектор dS : |
dS = F ×dt . |
|
(2.13) |
||
|
|
||||
Импульсом силы F за конечный промежуток времени от t0 |
до t на- |
||||
зывается вектор S : |
|
|
|
|
|
r |
t |
r |
t r |
|
|
S |
= òdS |
= ò F |
× dt |
(2.14) |
|
|
t0 |
|
t0 |
|
|
65
Проекции импульса силы на координатные оси могут быть вычислены по формулам:
Sx = òt |
Fx dt |
Sy = òt |
Fy dt |
Sz = òt |
Fz dt . |
(2.15) |
t0 |
|
t0 |
|
t0 |
|
|
Рассмотрим систему из п материальных точек с массами m1, m2 ,...,mn .
Освободимся от связей, заменив действие связей их реакциями, согласно принципу освобождаемости от связей. Обозначим через Fke = Fkxe i + Fkye j + Fkze k равнодействующую всех внешних сил, как заданных -
активных, так и реакций связей, действующих на точку mk .
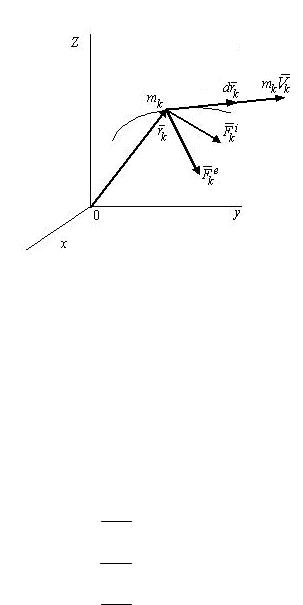
Обозначим, далее, через Fki равнодействующую всех внутренних сил, действующих на ту же точку (рис. 3.4). (k = 1, 2, ... , п.)
Рис. 3.4
Теорема об изменении количества движения системы материаль-
ных точек (в дифференциальной форме):
Производная по времени от количества движения системы материальных точек равна геометрической сумме всех внешних сил (как активных, так и реакций связи), действующих на систему.
dQ |
n |
r |
(2.16) |
= åFke |
|
||
dt |
|
||
k=1 |
|
|
|
В проекциях на оси координат:
ìdQx
ï dt
ïïdQy
í
ï dt
ïdQz ïî dt
n
= åFkxe
k=1 n
=åFkye .
k=1 n
=åFkze
k=1

66
Теорема об изменении количества движения системы материаль-
ных точек (в интегральной форме). Изменение количества движения системы за конечный промежуток времени равно сумме импульсов всех внешних сил, действующих на систему, за тот же промежуток времени.
где
r |
n |
r |
(t), |
Q1 |
= åmkVk1 |
||
|
k =1 |
|
|
r |
r |
n r |
Q1 |
−Q0 |
= åSke dt , |
k =1
r |
n |
r |
(0), |
Q0 |
= åmkVk0 |
||
|
k =1 |
|
|
(2.17)
(2.18)
Проецируя векторное равенство (2.17) на неподвижные инерциальные оси координат x, y, z, получим:
n
Q1x −Q0x = åSkeX k =1
n
Q1y −Q0 y = åSkeY (2.19)
k =1
n
Q1z −Q0z = åSkeZ . k =1
Закон сохранения количества движения.
Закон сохранения количества движения механической системы:
n r |
, |
то Q = const |
если: åFke = 0 |
k=1
Закон сохранения проекции количества движения на какую-либо ось (на-
пример, на ось х)
n
если: åFkeX = 0, то Qx = const
k=1
2.4. Теорема об изменении момента количества движения.
Момент количества движения и кинетический момент.
Момент вектора количества движения материальной точки относительно какого-либо центра (или оси) определяется точно так же, как момент вектора силы относительно центра (или оси).
Моментом количества движения материальной точки относитель-
но неподвижного центра О называется вектор, равный векторному произведению радиуса-вектора, соединяющего центр с точкой, на количество движения точки:
M |
r |
× mV . |
(2.20) |
0 (mV ) = r |
Кинетическим моментом (главным моментом количества движения), механической системы относительно центра O называется геомет-
67
рическая сумма моментов количеств движения всех точек системы относительно этого центра
r |
n r |
r |
). |
K0 |
= åM 0 |
(mkVk |
k=1
Моментом количества движения точки относительно оси х назы-
вается величина M x (mV ), равная проекции на эту ось вектора момента количества движения точки относительно любого центра Р, принадлежащего этой оси. Вычисляется M x (mV )так же, как момент силы относительно оси.
Кинетическим моментом системы относительно оси z называется проекция на эту ось кинетического момента системы относительно любого центра Р, принадлежащего оси:
n |
r |
) . |
K z = åM z |
(mkVk |
|
k=1 |
|
|
Кинетический момент Kz твердого тела, вращающегося относительно неподвижной оси z с угловой скоростью ω , вычисляется по формуле:
Kz = Izω ,
где I z - момент инерции твердого тела относительно оси z.
Теорема об изменении кинетического момента системы материальных точек:
Производная по времени от кинетического момента системы относительно неподвижного центра (неподвижной оси) равна сумме моментов всех внешних сил, действующих на систему, относительно того же центра (той же неподвижной оси).
dK |
0 |
n |
r |
r |
|
|
= åM 0 |
(Fke ) |
(2.21) |
||||
dt |
|
|||||
|
k=1 |
|
|
|
||
и выражает доказываемую теорему в векторной форме. Проецируя (2.21) на неподвижные (или инерциальные) оси Ох, Оу, Oz, получим:
dKx |
n |
r |
dK y |
n |
r |
dKz |
n |
r |
|
|
= åM x (Fke ), |
= åM y (Fke ), |
= åM z (Fke ), |
(2.22) |
|||||||
|
|
|||||||||
|
dt |
|||||||||
dt k |
1 |
k=1 |
|
dt k |
1 |
|
||||
= |
|
|
= |
|
||||||
здесь Kx, Ky, Kz – кинетические моменты системы материальных точек относительно неподвижных осей Ox, Oy, Oz соответственно:
n |
r |
n |
r |
K x = åM x (mkVk ) , |
K y = åM y (mkVk ) , |
||
k =1 |
|
k =1 |
|
n r
Kz = åM z (mkVk ) .
k =1
Формулы (2.22) выражают теорему об изменении кинетического момента в скалярном виде.
Если эту теорему применить к изучению движения твердого тела, вращающегося вокруг неподвижной оси Oz, получим дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси:
I zϕ = åM z (Fj ) , |
|
&& |
e |
|
|
68
где ϕ - угол поворота тела вокруг оси Oz.
Закон сохранения кинетического момента: если главный момент внешних сил системы относительно центра O равен нулю, то главный момент количеств движения относительно этого центра будет постоянным.
Например,
если |
n r r |
то |
r |
= const . |
åM 0 (Fke ) = 0, |
K0 |
k=1
Вправой части равенства располагается вектор-константа, т.е. и величина
вектора, и его направление не зависят от времени. Если сумма моментов внешних сил системы относительно какой-либо неподвижной оси равна нулю, то кинетический момент системы относительно этой оси остается постоянным.
Например,
если |
n |
r |
то |
Kz = const . |
åM z (Fke ) = 0, |
||||
k=1
2.5.Теорема об изменении кинетической энергии.
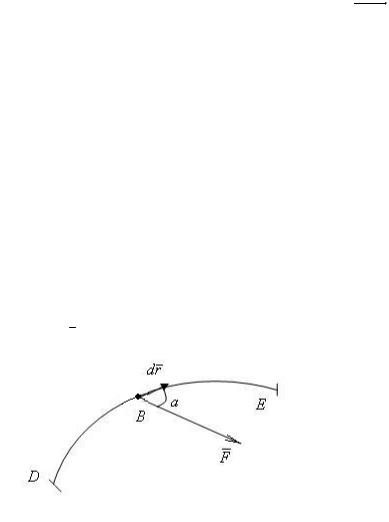
Элементарная работа. Рассмотрим точку В, перемещающуюся под действием системы сил. Перемещение точки вдоль траектории характеризуется вектором dr (рис. 3.5). Из системы выделим одну силу F .
Рис. 3.5
Элементарной работой силы F на перемещении dr называется ска-
лярная величина dA , равная скалярному произведению векторов F и dr
= × r = × × α . dA F dr F dr cos
В координатной форме элементарная работа подсчитывается по формуле:
dA = Fx dx + Fy dy + Fz dz,
где Fx , Fy , Fz , dx, dy, dz - координаты векторов F и dr соответственно.
Следует подчеркнуть, что, несмотря на принятую форму записи, элементарная работа dA не обязательно является полным·дифференциалом некоторой функции, зависящей от координат.
69
Знак элементарной работы определяется косинусом угла α : работа положительна для
0 £ α £ |
π |
, отрицательна для |
π |
£ α £ π |
и равна нулю при α = |
π . |
|
2 |
|
2 |
|
|
2 |
Вычисление элементарной работы в частных случаях.
1.Элементарная работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси z, находится по формуле:
dA = ±M z (F) ×dϕ ,
2. Сумма элементарных работ сил пары, приложенной к телу, вращающемуся вокруг неподвижной оси и при плоскопараллельном движении, может быть подсчитана так:
dA = ±M ×dϕ .
Здесь M – момент пары сил, dϕ - элементарный угол поворота тела. Знак «плюс» берется при одинаковых направлениях дуговых стрелок момента пары и направления вращения, «минус» - при различных направлениях (плоскость действия пары предполагается перпендикулярной оси вращения).
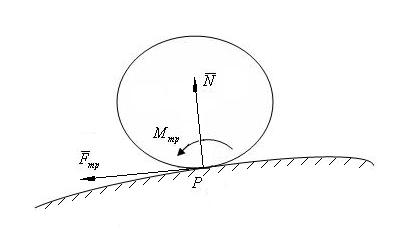
3. При вычислении элементарных работ сил трения, приложенных к телу, катящемуся без проскальзывания, необходимо учесть, что в точке касания P (рис. 3.6.) действуют: нормальная реакция N , сила трения Fтр и
момент сопротивления качению M тр = N ×k .
Рис. 3.6
Поскольку, в силу отсутствия проскальзывания, точка касания является
мгновенным |
центром скоростей |
и ее скорость Vp равна нулю, то и |
|
r |
=Vp dt = 0 , |
откуда: |
|
dr |
|
||
|
dA(N )= dA(Fтр )= 0, |
dA(M тр )= -M тр ×dϕ = -N ×k ×dϕ . |
|
Пример 1. Система элементарных сил тяжести твердого тела всегда имеет равнодействующую, равную G , приложенную в центре тяжести С.

70
Поэтому сумма элементарных работ сил тяжести равна работе силы тяжести на перемещении центра тяжести тела.
Пример 2. Сумма элементарных работ внутренних сил, приложенных к точкам твердого тела, равна нулю, так как главный вектор и главный момент системы внутренних сил равны нулю.
Работа силы. Потенциальная сила. Работа силы F на конечном перемещении точки по траектории DE (см. рис. 3.5) равна криволинейному интегралу:
r
A = òdA = òF ×dr = òFx dx + Fy dy + Fz dz .
DE |
DE |
DE |
Сила называется потенциальной, если ее работа не зависит от формы траектории, а зависит лишь от её начальной и конечной точек.
Примером потенциальной силы является сила тяжести G , ее работа может быть подсчитана по формуле:
A = -G(z - z0 ) .
Здесь ось z выбрана параллельно линии действия силы тяжести и направлена ей навстречу, G - сила тяжести, z0 , z - координаты начальной и
конечной точек траектории.
Кинетическая энергия. Кинетической энергией точки массы т,
движущейся со скоростью V , называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости
mV2 2 .
Кинетической энергией механической системы называется сумма кинетических энергий всех ее точек:
T = ån mkVk .
k=1 2
Формулы для вычисления кинетической энергии твердого тела:
а) при его поступательном движении: |
|
T = |
|
mV 2 |
|
; |
|
|||||
|
|
|
|
C |
|
|
||||||
|
|
|
2 |
|
|
|
||||||
б) при вращении вокруг неподвижной оси z: |
|
|
|
|
|
|
|
|
|
|
|
|
|
T = |
Izω2 |
|
; |
|
|||||||
в) при плоскопараллельном движении: |
|
|
mV 2 |
2 |
|
|
|
|
ω2 |
|||
|
|
|
|
I |
C |
|||||||
|
T = |
|
|
C |
+ |
|
|
|
. |
|||
|
2 |
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|||||
где VC - скорость центра масс тела, а IC - момент инерции тела относи-
тельно оси, перпендикулярной основной плоскости и проходящей через центр масс С.
Теорема об изменении кинетической энергии системы матери-
альных точек (в дифференциальной форме). Дифференциал кинетической энергии системы равен сумме элементарных работ всех сил, действующих
