Добавил:

posterp Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет железнодорожного транспорта им. академика В. Лазаряна

Предмет:

Высшая математика

Файл:

Частина 3

.pdf

Скачиваний:

Добавлен:

26.04.2021

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

“Курс вищої математики. Частина 3.”

1.5

0.5

1.5

-0.5

Приклад. Знайти загальний інтеграл рівняння x( y2

−1)dx + y(x2

−1)dy = 0 .

Це рівняння із змінними, що розділяються.

xdx

ydy

= 0;

∫

xdx

= −∫

ydy

;

−

ln x2 −1 + ln y 2 −1 = ln C;

Загальний інтеграл має вигляд:

Побудуємо інтегральні криві диференціального рівняння при різних значеннях С.

З = - 0,5	З = -0,02	З = -1	З = -2
		2
		1.5
		1
		0.5
-2	-1		1	2
		-0.5
		-1
		-1.5
		-2
	З = 0,02	З = 0,5З = 1		З = 2
Приклад. Знайти вирішення диференціального рівняння, що задовольняє
заданим початковим умовам.

“Курс вищої математики. Частина 3.”

y′cos x = ( y +1)sin x;

y(0) = 0.

Це рівняння із змінними, що розділяються.

y′

sin x

;

= tgxdx;

y +1

y +

cos x

∫

= ∫tgxdx;

y +1

= −ln

cos x

+ ln C;

y +

(y +1) cos x

= ln C;

(y +1) cos x = C;

Загальне рішення має вигляд

: y =

−1.

cos x

Знайдемо приватне рішення за заданої початкової умови у(0)= 0.

			0 =	С	−1;	C =1.
			0 =	1	−1;	C =1.
				1

Остаточно отримуємо: y	=	1	−1.
Остаточно отримуємо: y	=	cos x	−1.
		cos x

Приклад. Вирішити попередній приклад іншим способом.

Дійсно, рівняння y′cos x = ( y +1) sin x

може

бути

розглянуте як лінійне

неоднорідне диференціальне рівняння.

y′cos x − y sin x = sin x.

Вирішимо відповідне йому лінійне однорідне рівняння.

′

cos x − y sin x = 0;

′

cos x

= y sin x;

= tgxdx;

∫

= ∫tgxdx + ln C;

= −ln

cos x

+ ln C;

y cos x = C;

y =

cos x

Вирішення неоднорідного рівняння матиме вигляд: y = cosC(xx) .

Тоді y′ = C′(x) cos x + C(x)sin x . cos2 x

Підставляючи в початкове рівняння, отримуємо:

′

C(x)sin x

[C (x) cos x + C(x)sin x] cos x

−

= sin x;

′

cos2 x

cos x

′

C (x) cos x

C(x) = ∫sin xdx = −cos x + C;

= sin x;

C x)

= sin x;

cos x

−cos x +C

Разом y =

;

y =

−1;

cos x

“Курс вищої математики. Частина 3.”

З урахуванням початкової умови у(0)= 0 отримуємо y = cos1 x −1;

Як видно результати, отримані при вирішенні даного диференціального рівняння різними способами, співпадають.

При вирішенні диференціальних рівнянь буває можливо вибирати метод рішення, виходячи з складності перетворень.

Приклад. Вирішити рівняння

′

+ y cos x

= 2 sin 2x з початковою умовою у(0)=

Це лінійне неоднорідне рівняння. Вирішимо відповідне йому однорідне рівняння.

y′+ y cos x = 0;

= −cos xdx;

= −sin x +C1 ;

y = e−sin x eC1 ;

y = Ce−sin x ;

Для лінійного неоднорідного рівняння загальне рішення матиме вигляд: y = C(x)e−sin x ;

Для визначення функції З(х) знайдемо похідну функції у і підставимо її в початкове диференціальне рівняння.

′

= C

′

−sin x

−C

(x)e

−sin x

cos x;

(x)e

′

−sin x

−C(x)e

−sin x

cos x +C(x)e

−sin x

cos x = sin x cos x;

C (x)e

′

−sin x

= sin x cos x;

′

sin x

sin x cos x;

C (x)e

C (x) = e

= e

sin x

;

dU = cos xdx;

С(x) = ∫esin x sin x cos xdx

∫esin x cos xdx =

sin x

= esin x sin x −

cos xdx;

dV = e

U = sin x;

=esin x sin x − esin x + C.

Разом y = e−sin x (esin x sin x −esin x

+C);

y = sin x −1+Ce−sin x ;

Перевіримо отримане загальне рішення підстановкою в початкове диференціальне рівняння.

cos x +Ce−sin x (−cos x) +sin x cos x −cos x +Ce−sin x cos x = sin x cos x; (вірно)

Знайдемо приватне рішення при у(0)= 0.
0 = sin 0 −1+Ce0 ;	C =1.

Остаточно y = sin x + e−sin x −1.

Приклад. Знайти вирішення диференціального рівняння

20xdx −3ydy = 3x2 ydy −5xy2 dx

з початковою умовою у(1)= 1.

“Курс вищої математики. Частина 3.”

Це рівняння може бути перетворене і представлене як рівняння з розділеними змінними.

20x −

3yy

′

= 3x

′

−5xy

;

′

+1) = 5x( y

+ 4);

3yy

y′

;

dy =

dx;

y 2 + 4

x2 +1

y 2 + 4

x2 +1

∫

dy = ∫

dx;

+ 4

ln( y 2

+ 4) =

ln(x2

1) + ln C

( y 2 + 4)3 = C (x2 +1)5 ;

y 2 + 4 = C 3 (x2 +1)2 ;

y2 = C(x2 +1)

− 4;

y = 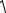C(x2 +1) 3 − 4;

З урахуванням початкової умови:

5														125 = 8C 3 4; C 3 =	125
1 = С 2	3	− 4 =	С3		32 − 4;					1 = 2C3 4 − 4;		5 = 2C3	4;	125 = 8C 3 4; C 3 =	125	;
											5 .				32
										C =	5 .
											23	4
								5
						2	+1		3
Остаточно		y =		x			+1			− 4.

			5				2
							2
Приклад.			Вирішити							диференціальне		рівняння	xy′+ y = x +1 з початковою

умовою у(1)= 0.

Це лінійне неоднорідне рівняння.

Вирішимо відповідне йому однорідне рівняння.


	′		xdy		dy		dx
xy	′	+ y = 0;	dx = −y;		y = − x ;
xy		+ y = 0;	dx = −y;		y = − x ;
				xy = C;		y =		C
				xy = C;		y =		x
								x

Вирішення неоднорідного рівняння матиме вигляд: y = C(xx) ;

Підставимо в початкове рівняння:

x	C′(x)x −C(x)	+	C(x)	= x +1;	C′(x)x
	x2		x		x

ln y = −ln x + ln C;

;

= x +1; C′(x) = x +1;

C(x) = x2 + x +C; 2

Загальне рішення матиме вигляд: y = 2x +1+ Cx ;

“Курс вищої математики. Частина 3.”

C обліком початкової умови у(1)= 0:

0 =

+1+ C;

C = −

;

Приватне рішення

: y =

−

+1;

Приклад. Знайти

вирішення

диференціального

рівняння

xy′ = y ln

початковою умовою у(1)= е.

Це рівняння може бути приведене до виду рівняння із змінними, що

розділяються, за допомогою заміни змінних.

Позначимо:

Рівняння приймає вигляд:

′ u

+ e

= e

′

+1 = u;

′

= u −1;

xu e

Отримали рівняння із змінними, що розділяються.

= u −1;

;

u −

∫

;

u −1

= ln

+ ln C;

u −1 = Cx;

u −1

Зробимо зворотну заміну:

Cx+1

Cx = ln

−1;

= Cx

+1;

= e

;

Загальне рішення

: y = xeCx+1;

e = eC+1;

C = 0;

C обліком початкової умови у(1)= е:

Приватне рішення

: y = ex;

Другий спосіб рішення.

′

= y ln x ;

xy′ = y ln y − y ln x;

y′

−

ln y = −

ln x;

Отримали лінійне неоднорідне диференціальне рівняння. Відповідне однорідне:

y′−

ln y = 0;

d(ln y)

y′ =

ln y;

;

∫

= ∫

;

y ln y

ln y

= ln

+ ln C;

ln y = Cx;

y = eCx ;

Вирішення початкового рівняння шукаємо у вигляді:

y = eC ( x) x ;

Тоді y

′

= e

C ( x) x

′

(C (x)x +C(x));

Підставимо отримані результати в початкове рівняння:

“Курс вищої математики. Частина 3.”

xeC ( x) x (C′(x)x +C(x))= eC ( x) x ln eC ( x) x ; x

x2C′(x) + xC(x) = C(x)x − ln x;

′

ln x

(x)

= −ln x;

C (x)

= −

;

ln x

u = ln x;

dv =

;

ln x

− dx

C(x) = −∫

∫

dx =

= − −

−

du =

;

v = −

;

y = eC ( x) x = eln x+1+Cx = xeCx+1 ;

Отримуємо загальне рішення:

y = xeCx+1

;

′

Приклад.

Вирішити

диференціальне

рівняння

+ e

− x

умовою у(1)=0.

У цьому рівнянні також зручно застосувати заміну змінних.

lnxx + 1x +C;

= 0 з початковою

′

xu′

= u;

x = ln u;

y = x ln u;

= ln u

+ u

;

Рівняння приймає вигляд:

du2 = − dx ;

∫du2

= −∫dx;

xu′ = −u 2 ;

= ln

+ ln C;

= ln Cx;

Робимо зворотну підстановку: e−

= ln(ln Cx);

= ln Cx;

−

Загальне рішення

: y = −x ln(ln Cx

);

C обліком початкової умови у(1)= 0:

0 = −ln(ln C);

C = e;

Приватне рішення:

y = −x ln(ln ex);

Другий спосіб рішення.

′

+ e

− x = 0

Заміна змінною: u =

;

′

−u = 0

u x + u + e

′

= 0

u x + e

dudx x = −eu

“Курс вищої математики. Частина 3.”

− e−u du = dxx

−∫e−u du = ∫dxx ;

e−u = ln

+ ln C;

e−u = ln

;

−u = ln(ln

);

u = −ln(ln

);

Загальне рішення: y = −x ln(ln Cx);

Геометрична інтерпретація вирішень диференціальних рівнянь першого порядку.

уа

A S

Як вже мовилося вище (див. Интегральные кривые. ), лінія S, яка задається функцією, каким-, що є, або вирішенням диференціального рівняння, називається інтегральній кривій рівняння y′ = f (x, y).

Похідна у’ є кутовим коефіцієнтом дотичної до інтегральної кривої.

У будь-якій крапці А(х, у) інтегральній кривій цей кутовий коефіцієнт дотичної може бути знайдений ще до вирішення диференціального рівняння.

Оскільки дотична указує напрям інтегральній кривій ще до її безпосередньої побудови, то за умови безперервності функції f(x, у) і безперервного переміщення крапки А можна наочно зобразити поле напрямів кривих, які виходять в результаті інтеграції диференціального рівняння, тобто є його загальним рішенням.

Визначення. Безліч дотичних в кожній точці даної області називається полем

напрямів.

З урахуванням сказаного вище можна привести наступне геометричне тлумачення диференціального рівняння:

1)Задати диференціальне рівняння першого порядку – це означає задати поле

напрямів.

2)Вирішити або проінтегрувати диференціальне рівняння – це означає знайти всілякі криві, у яких напрям дотичних в кожній крапці співпадає з полем напрямів.

Визначення. Лінії рівного нахилу в полі напрямів називаються ізоклинами.

Чисельні методи вирішення диференціальних рівнянь.

Відомі методи точної інтеграції диференціальних рівнянь дозволяють знайти рішення у вигляді аналітичної функції, проте ці методи застосовні для дуже

“Курс вищої математики. Частина 3.”

обмеженого класу функцій. Більшість рівнянь, що зустрічаються при вирішенні практичних завдань не можна проінтегрувати за допомогою цих методів.

У таких випадках використовуються чисельні методи рішення, які представляють вирішення диференціального рівняння не у вигляді аналітичної функції, а у вигляді таблиць значень шуканої функції залежно від значення змінної.

Існує декілька методів чисельної інтеграції диференціальних рівнянь, які відрізняються один від одного по складності обчислень і точності результату.

Розглянемо деякі з них.

Метод Ейлера.

(Леонард Ейлер (1707 – 1783) швейцарський математик )

Відомо, що рівняння y′ = f (x, y) задає в деякій області поле напрямів.

Вирішення цього рівняння з деякими початковими умовами дає криву, яка стосується поля напрямів в будь-якій крапці.

Якщо узяти послідовність точок х0, х1, х2 .. і замінити на відрізках, що вийшли, інтегральну криву на відрізки дотичних до неї, то отримаємо ламану лінію.

M1 M3

y0 M4

При підстановці заданих початкових умов (х0, у0) в диференціальне рівняння y′ = f (x, y) отримуємо кутовий коефіцієнт дотичної до інтегральної кривої в

початковій точці

tgα0 = y′ = f (x0 , y0 ).

Замінивши на відрізку [x0, x1] інтегральну криву на дотичну до неї, набуваємо значення

y1 = y0 + f (x0 , y0 )(x1 − x0 ).

Проводячи аналогічну операцію для відрізання [x1, x2], отримуємо:

y2 = y1 + f (x1 , y1 )(x2 − x1 ).

Продовжуючи подібні дії далі, отримуємо ламану криву, яка називається

ламаною Ейлера.

Можна записати загальну формулу обчислень:

yn = yn−1 + f (xn−1 , yn−1 )(xn − xn−1 ).

Якщо послідовність точок хi вибрати так, щоб вони отстояли один від одного на однакову відстань h, зване кроком обчислення, то отримуємо формулу:

yn = yn−1 + f (xn−1 , yn−1 )h

Слід зазначити, що точність методу Ейлера відносно невисока. Збільшити точність можна, звичайно, зменшивши крок обчислень, проте, це приведе до ускладнення розрахунків. Тому на практиці застосовується так званий уточнений метод Ейлера або формула перерахунку.

“Курс вищої математики. Частина 3.”

Суть методу полягає в тому, що у формулі y1 = y0 + f (x0 , y0 )h замість значення y0′ = f (x0 , y0 ) береться середнє арифметичне значень f(x0, y0) і f(x1, y1). Тоді уточнене

значення:

f (x0 , y0 ) + f (x1 , y1 )

y(1)

= y

Потім знаходиться значення похідної в крапці (x

, y(1) ) . Замінюючи f(x0, y0)

середнім арифметичним значень

f(x0,

y0)

і f (x , y(1) ) ,

знаходять друге уточнене

значення у1.

f (x

, y

) + f (x , y(1) )

y(2)

= y

Потім третє:

f (x

, y

) + f (x , y(2) )

y(3)

= y

і так далі поки два послідовні уточнені значення не співпадуть в межах заданого ступеня точності. Тоді це значення береться за ординату точки М1 ламаною Ейлера.

Аналогічна операція проводиться для решти значень у.

Подібне уточнення дозволяє істотно підвищити точність результату.

Метод Рунге – Кутта.

Метод Рунге – Кутта є точнішим в порівнянні з методом Ейлера.

Суть уточнення полягає в тому, що шукане рішення представляється у вигляді розкладання в ряд Тейлора. (Див. Формула Тейлора. )

′	′′	h2	′′′	h3	IV	h4
					+ yi	4! +...
yi+1 = yi + yi h + yi		2! + yi 3!
Якщо в цій формулі обмежитися двома першими доданками, то отримаємо

формулу методу Ейлера. Метод Рунге – Кутта враховує чотирьох перших членів розкладання.

yi+1 = yi + yi′h + yi′′h2 + yi′′′h3 = yi + ∆yi . 2! 3!

У методі Рунге – Кутта приросту ∆yi пропонується обчислювати за формулою:

∆yi = 16 (k1(i) + 2k2(i) + 2k3(i) + k4(i) )

де коефіцієнти ki обчислюються по формулах:

	k1(i) = hf (xi , yi );
(i)			h		(i)
					k1
k2	= hf	xi +		; yi +		;
			2		2

(i)			h		(i)
					k2
k3	= hf	xi +		; yi +		;
			2		2

k4(i) = hf (xi + h; yi + k3(i) );

Приклад. Вирішити методом Рунге – Кутта диференціальне рівняння y′ = x + y за початкової умови у(0)= 1 на відрізку [0; 0,5] з кроком 0,1.

“Курс вищої математики. Частина 3.”

Для i = 0 обчислимо коефіцієнти ki.

k1(0) = hf (x0 , y0 ) = 0,1(x0 + y0 ) = 0,1(0 +1) = 0,1;

(0)

= hf x0

; y0

= 0,1(0,05 +1,05)= 0,11;

(0)

= hf

x0 +

; y0

= 0,1(0,05 +1,055) = 0,1105;

k4(0)

= hf (x0 + h; y0

+ k3(0) )= 0,1(0,1 +1,1105) = 0,1211;

∆y

(k (0)

+ 2k (0)

+ k (0) ) =

(0,1+ 0,22 + 0,221+ 0,1211) = 0,1104;

x1 = x0 + h = 0,1;

y1 = y0

+ ∆y0

=1+ 0,1104 =1,1104;

Подальші обчислення приводити не будемо, а результати представимо у вигляді таблиці.

i	xi		до	∆yi	yi
0	0	1	0,1000	0,1104	1
0	0	2	0,1100	0,1104	1
		3	0,1105
		4	0,1155
1	0,1	1	0,1210	0,1325	1,1104
1	0,1	2	0,1321	0,1325	1,1104
		3	0,1326
		4	0,1443
2	0,2	1	0,1443	0,1569	1,2429
2	0,2	2	0,1565	0,1569	1,2429
		3	0,1571
		4	0,1700
3	0.3	1	0,1700	0,1840	1,3998
3	0.3	2	0,1835	0,1840	1,3998
		3	0,1842
		4	0,1984
4	0,4	1	0,1984	0,2138	1,5838
4	0,4	2	0,2133	0,2138	1,5838
		3	0,2140
		4	0,2298
5	0,5				1,7976

Вирішимо цей же приклад методом Ейлера.

Застосовуємо формулу yn = yn−1 + hf (xn−1 , yn−1 ).

x0 = 0, y0 =1,

f (x0 , y0 ) = x0 + y0 =1;

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
26.04.20211.64 Mб3M-008.pdf
#
26.04.20211.23 Mб3M-040.pdf
#
26.04.2021439.24 Кб5M-051.pdf
#
26.04.2021967.56 Кб12Частина 1.pdf
#
26.04.2021882.81 Кб2Частина 2.pdf
#
26.04.20211.01 Mб2Частина 3.pdf
#
26.04.2021669.46 Кб6Частина 4.pdf