Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

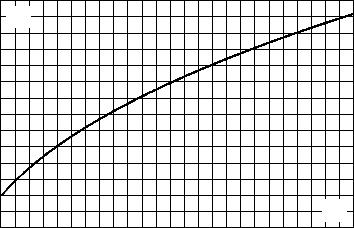
з Ÿ46При. великих значеннях квàнтового числа

4

En = 4 3

m2

n

2Такудо

n

, n 1.

3 1/3

2α~4

1/3

4/3

Ÿ30),жзалежнiстьiншда¹èмi чискваловизiкламсичнеое наближенняiцi¹нтом:замiсть(див. Приклад

4/3

оскiлькиому¹мочастота

/2 = 1.092535

. Зауважимо,

1ùî.081687

[3√π (3/4)/ (1/4)]

òî÷íi

En

íiæ

значення, якi да¹

наближення¹длянижчими,

n 1.

0*

ис. 50. Залежнiсть енер i¨

Величипараметр

E вiд параметра ангармонiзму λ.

осцилято

à, ¹E

, тобто вiдноше ня

En

унiверсальною ункцi¹ю параметрадоенерi¨ гармонiчного

суючивиз ача¹

íер етичнийангармонiзмуспектр а гармонiчного осцилятора:λ ïîâíiñòþiê

ченнi квантового числа

λ0 = 6α~/m2ω3 при заданому зна-

452

n, обчислю¹мо величину λ

ω′/ω, ïiñëÿ

осцилятора. 50визна. . ра iк залежностi

E

вiд параметра

λ

прадiальногочармонiчногоданоФункцiязнах èìîñ E

En

-

лятора

(див.рухуŸ40)да¹усередненняча¹.спеПоажемотрзнерозмiреногоцеiй.Длядляпросторовогоператора-вимi нîенергосцианi¨

E

N

2E

d2

l(l + 1)

2α

~

2

ρ4!

= −

+

+ ρ2

+

~ω

dρ2

ρ2

~ω

mω

невiдомоюк димординатзчастотою.хвильовимиОскiлькиу ункцiями

середнення,

ρгаяке=ìîíi÷íìèr mω/познаго~

чили,осцилятораr рискою,радiальназпров

åéòè ä íîâî¨ çìiííî¨

, то природно

ïåð

p

ρ′ = rp

= ρp

ω′

:

2E

ω

−

d

l(l + 1)

ω

=

′

+

+ ω′

ρ2

~ω

ω

dρ2

ρ2

ω

2 2α

~

2

+

просторовогоштрих з ново¨ãàðçìiíìîíi÷íî¨ îïóñго осцилякà¹ìî.òîðÎñêiëа середн¹üêè, ÿê ìè çíà¹ìî, äëÿ

−

d2

l(l + 1)

+ ρ2 = 2 2n + l +

3

,

+

dρ2

ρ2

2

~ω

=

ω′ 2 2n + l +

2

− ρ2 +

ω′ ρ2

2E

3

ω

Потрiбнi середнi +

ω′

~ω

mω

2

ρ4.

ω

2 2α

~

доданка:

ρ2

âîãî,

l ρ2/2

2

n

3/4

рекурентне¯ спiввiдношення,

узагальнених полiномiв Ла ерра:i

Cnρ e−

Ln

(ρ ) Cn

= äëÿ(−) (mω′/~)

p2n!/ (n + l + 3/2)

2 ¯ν

2

¯ν

2

) −

¯ν

2

)

ρ Ln(ρ

) = (2n + ν + 1)Ln(ρ

(n + 1)Ln+1

(ρ

¯ν

2

)

− (n + ν)Ln−1(ρ

νèêîì= l + 1/2

. Помножимо це рiвняння на ¯ν 2

) з ваговим множ

ρ2 проiнтеункцiй ру¹мо за

Ln(ρ

2

2l

e−

r

ìà¹ìî,Cçàρ

. У результатi з лiвого б ку

n

означенням,

-

íiсть хвильових

, залишпрà¹тьсявраховуючилишевнесокортонормовавiдпершого

ЗлiваПiдносимовадраттимемо,множимотеперобидвiзаознаρòîé= 2n + l + 2

.

2

3

самийрекурваговийåнтногомн жникспiввiдношенняйiнтеаслiдокру¹мо.

частиниченням,

êè çíè-

ρ

2

2

2

2

2

4

àáî,ρ

=пiдставляючи(2n + ν + 1)ñþäè+ (nвеличини+ 1) (Cn/Cn+1)

+ (n + ν) (Cn/Cn−1) ,

Cn, äiñòà¹ìî

2

4

монiТеперногоρ

бачимо,=осцилятора(2n +ùîν +вираз1) + (äëÿn +åíåð1)(n +i¨,νвiднесено¨+ 1) + (n +äîνåíåð) n. i¨ ãàð

âåëè÷èíîþ

~ω(2n + l + 3/2), ормально збiга¹ться з

íèì

рiвняннямдляна

дновимiрного осцилятора з тим самим кубiч-

E

ω′/ω, але з iншим параметром

до просторуλ =ä ~ω

mω

2

ρ .ρ .

4α

~

4

2

Перехiд

îâiëü

¨

вимiрностi

критими очима простою за

íîþ (äèâ. Ÿ44) N çäiéñíþ¹ìî iç çà-

остаточно рiвнi енер i¨

l íà l + (N − 3)/2, i

N -âèìiрного ангармонiчного осцилятора

454

En,l = ~ω 2n + l +

N

E ,

2

(2n + l + N/2)2 + (n + 1)(n + l + N/2) + n(n + l + N/2

−

1)

Îòæå,

задаючи розмiр iс ь простору

.

×

2n + l + N/2

точнихдимо

Nнарештi,квантовi числа (n, l), çíà

Ïðè λ,

í ÷à¹ìî

ω′/ω

,

i

E ò

En,l.

якимпараметрвиз

N → ∞

λ = 2α~N/m2ω3

å åð iÿ En,l/N =

1/3

4

2

èìЗробиморезубiльша. татомвимiрнiстьзауваженнядля цi¹¨системи,щодомежi.розмТомутимрробимоí, остiашi резульросторувисновокзбiга¹тьсяатиадiальномупроближчiте,зточщо

ì'ÿòà¹ìî (äèâ. Ÿ44), ùî ïðè ï ðåõ äi â

N = 1. Ïà-

рiвняннi до

N -âèìi

îìó

N = 1 ми матимеквантовихпри l = 0 ïàðíвiдтворю¹моункцi¨ змiн

¨

xвимiрнiбути,а прирозв'язкиl = 1 непарнiдлявсiх. Тиîìóсам мчиселзвiдси

повинн -

одновимiрне

n. Ëåãê

бачити, що

ç

λ ïðè çàìiíi

ü

n íà 2n çáiãà¹òüñÿ, ÿê

скiльки положення рiвновагиосциляторав3, акiйдамосистемiпiдккузмiщу¹тьсдля¨¨розв'язкуточки.

βx

x = 0

деяку точку

x = x0

âó óíêöiþ ã

,

взяти

природнозалжною вiдпробну хвиль

Отже, матимемо

ва варiацiйнi параметри: частоту x′

= x

−

x0.

íàòó

ω′

i

оорди

â ðàç, ÿêèé

è ìàëè âèùå äëÿ

дновимiрного випадку

à òîòè

ω

íà

аточний

2 1/2

. Ìiíiìiçàöiÿ çàìiíîþ¨¨

вжльовихтона

ω[1 + 6x0(β + 2αx0)/mω ]

x0

-

÷iäèñельнимиМичасу,небачили,залежитьтоункцiйвипадкуŸзнайтимето55що. дамиТеорiявiддляявномуточнийчасуда¹стацiонарнихзбурень,вда¹тьсоствиглядiîзв'язок.залежнихзнайтиЯкщостанiв,рiвняннярезультатгамiльчасовуколивiдШредин.оператортонiанчасузалежнiстьзалежитьераамiльМовахви

ã

íåìî

. Причо

ó îñêiëüêè åíåð iÿ âæ

íå

Отжальномуе, з дача зводитьсяжливше до знах джен я хвильових кцiй

¹

ð ëîì ðóõó, òî çìiíþ¹òüñ

é ñà

постановк

задачi.

.

iнтене мож

пр обч слення

ласних

÷åíü ãàìiëü

усистемибудь-якийчаенмомент часу t

. ßêùî â ãàìiëü

iàíi

ˆ

äîñëiäæóâàíî¨

òîíiàíîìçíà

H

òîíi

íÿ íа власнi Eзначенняn та хвильовiтавласнióíêóíêöi¨öi¨ ψn оператора(q) визнача¹мо з рiвнян-

з визна ëü îþV =частиноюV (t), залежний вiд часу t, ¹ малим п

ÿ íi

реньНехай. задана система

H0амiль,томожна побудувати теîðiþ çáó

цеозв'язокстацiонарнiхвильстани:

ˆ

домийвiд часу.

H0

-

ового рiвняння Шредин, щоераненамзалежитьужвi

iâ i åíåð i¨

ψn(0)(q, t) = e− ~ En(0)tψn(0)(q).

(0)

(0)

ˆ

Нехай на систему накладˆ

H0:

¹ться залежне вiд часу збурення

(0)

(0)

(0)

H0ψn

(q) = En

ψn (q).

так що повний гамiльтонiàí

ˆ

V (t),

i~

ˆ

456

∂t

= Hψ(q, t).

E

(0)t (0)

авимоiд розклвiдомогоцейчастознайтирдузкладназиваютьметоочевидрiвнянняду рiвнянняозалежатьметодля~ äènомШрединвiдеренцiальних.варiацiйЦейчасупiдхiд,ера:.Длясталихщорозв'язкурiвнянь.запроНазва.-

n

òåîði¨

X

ni~C˙ n(t) e−

n

~ En(0)tψn(0)(q) + Cn(t)En(0) e− ~i En(0)tψn(0)(q)o

X

Крапкою над

En(0)t

ˆ

(0)

i

En(0)t

ˆ

(0)

~

~

ψn

(q) + Cn(t) e−

=

n

nCn(t) e−

H0

V (t)ψn (q)o .

X

Помножимогий член у лiвiйобидвi

частинипозначенарiвняннярiвнянняпохiднаскорочу¹тьназачаñяомз.першимЯкбачимо,уп авiйдру-.

Cn(t)

частиíi

çà

ψm(0) (q) i ïðîiíòå ðó¹ìî

q:

матричний ˙елемент~

En(0)t

i

En(0)t

~

äå

оператора збурення

Vmn(t),

n

n

X

X

Перепишемо наше

ˆ

òàê:

(0)

ˆ

(0)

(q) dq.

Vmn(t) = hm|V (t)|ni

= Z

ψm (q)V (t)ψn

рiвняння

˙

˜

i~Cm(t) =

n

Cn(t)Vmn(t),

X

де частоти

˜

iωmnt

Vmn(t),

Vmn(t) = e

ωmn =

Em(0) − En(0)

.

457

~

t = t0

залежатиму

t = t1 ðiçíèöi

îцiкавить,обтому¨а,ж,нетобтстанiкiнвiдщо-

Мiж iншим, величини ˜

елементами оператора

Vmn(t) ¹ нiчим iншим, як матричними

ìîâà â Ÿ19:

ˆ

V (t) у зображеннi вза¹модi¨, про яке йшла

âiä

òîíiàí

Припустимо, ˜

ˆ

ˆ

~

вмика¹тьсяСпостережуваль~ деякий мом нт часу

Vщо (збуренняt) = m e

H0t

V (t) e−

H0t

n .

mn

h

|

|

зрозумiло,вимика¹ться в момент

i величини,

ëèøå âiä .

τ = t1

− t0

оскiлькисистемун

öåтого,збурено¨,вийнеколиматимее ектзвонохопитьшзадачiзалежатимемiсцяоператорвмикзалежитьзбуренняа¹тьсвипадкувiдчи.того,кАвимиоличасуякнасг.а¹тьсяТутмiльдовгоцейважлив.дi¹випадокОчезбурення,нульовидноне.яктакТ

Отже, прийма¹мо,

ˆ

ежить вiд часу.

H0

íå çà

ùî

Таким чином, при

0,

t < t0,

t > t1.

Vˆ (t) =

Vˆ (t), t0 ≤ t

≤ t1

,

якому початковомуt < t0

станi наша iзична система перебува¹ в де-

( nal)

Cf (t). Запишемо рядкiнцевоготе рi¨ збурень

(0)

номер стану, у якомуψ(пребува¹q, t) = ψ система(q, t), . À ïðè

t > t1

iндексукупнiсть

ψ q, t) = ψ(0)

(q, t),

f

початкпозначаовий-

(initial)ютьТеперf азапитаймо:кiнцевийномерквантовихцьогодоякогостанучисел,стани.жIндекси.щохарактеризуютьстануf скорочено

iд дi¹ю збурення

ˆ

f прийде система

− t0

V (t) çà ÷àñ τ = t1

458

Cn(t) = Cn(0)(t) + Cn(1)(t) + Cn(2)(t) + · · · .

ðåííÿ

íаючийогозпершо¨,пам'ятiдорiвнюють.Привiдсутностiнулевi,збу-

âсi поправки,λ тримаючипочи

(ν)

ÿê(t) i=â0стацiонарнiй, ν = 1, 2, .òåîði¨. . , збурень,

а нульове наближення,C

n

(0)

Прирiвнюючи злiва i справаC

â(tрiвняннi) = δ . äëÿ

íÿ ü:

рiвняння

n

ni

îê ðiâ-

, отриму¹мо такий ланцю

λ

˙ (1)

(0)

˜

~Cm

(t) =

n Cn (t)Vmn(t),

~C˙m(2)(t) =

Pn Cn(1)(t)V˜mn(t),

З першого

. . . . . . . . . . . . .

. . . . . . . . P

ìà¹ìî

˙ (1)

˜

i~Cm

(t) = Vmi(t)

ïëiòóÌè çí

Cm

(t) = i~

Zt0

Vmi(t′) dt′.

à ñàìå:

t

наближеннi,

àì

дайшлиймовiрностiозв'язоктого,задачiщо çàв першомучас˜

(1)

1

менту

τ = t1 − t0 дi¨ збурення з мо-

t0 äî t1 система перейшла зi стану i â ñòàí f

Âiäïîâiäíî

Cf

= i~

Zt0

Vf i(t′) dt′.

(1)

1

t1

éìîâiðíiñòü òàêîãî переходу˜

àáî â ÿâíié îðìi

2

Wi→f

t1

2

1