
- •Введение
- •Информация, сообщения, сигналы
- •Блок-схема передачи информации
- •Краткая история и примеры устройств передачи различных сообщений
- •Классификация сигналов
- •Количество информации дискретных сообщений
- •6.1 Свойства энтропии источника
- •6.1.1 Энтропия максимальна и равна:
- •6.1.2 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.
- •6.1.4 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.
- •6.2 Двоичный дискретный источник
- •Количество информации непрерывных сообщений
- •Статистически зависимые источники сообщений
- •Практические приложения теории информации
- •9.1 Сигнал и аддитивная помеха
- •9.2 Кодирование дискретных сообщений
- •9.3 Эффективное первичное кодирование
- •9.2.1 Метод укрупнения алфавита
- •9.2.2 Методы статистического кодирования
- •9.2.3 Кодирование в биологических структурах
- •Курсовая работа по теории информации
6.2 Двоичный дискретный источник
Очень часто, рассматривая источники сообщений, мы имеем дело с, так называемыми, двоичными источниками, вырабатывающими кодовые слова по основанию 2. Очень интересно оценить энтропию такого рода источников или, как часто говорят, энтропию двоичного ансамбля. Под определением ансамбля понимают то, что заданы не только значения сообщений, вырабатываемых источником, но и их вероятности.
Итак,
пусть m=2,
и это означает, что речь идет о двоичным
источнике. Заданы также вероятность
появления нулевого элемента
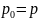 и, следовательно, вероятность единицы
и, следовательно, вероятность единицы
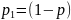 .
Это соотношение очевидно, поскольку мы
знаем, что существует условия нормировки,
состоящее в том, что сумма вероятностей
всегда должна равняться единице.
.
Это соотношение очевидно, поскольку мы
знаем, что существует условия нормировки,
состоящее в том, что сумма вероятностей
всегда должна равняться единице.
Мы можем записать формулу, которая определяет энтропию источника:
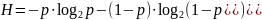 (16)
(16)
Как было показано энтропия максимальна, когда сообщения появляются с равной вероятностью. Поскольку наши сообщения либо 0, либо 1, то максимум достигается тогда, когда вероятность появления 0 равна вероятности появления единицы и равна 0,5.
.
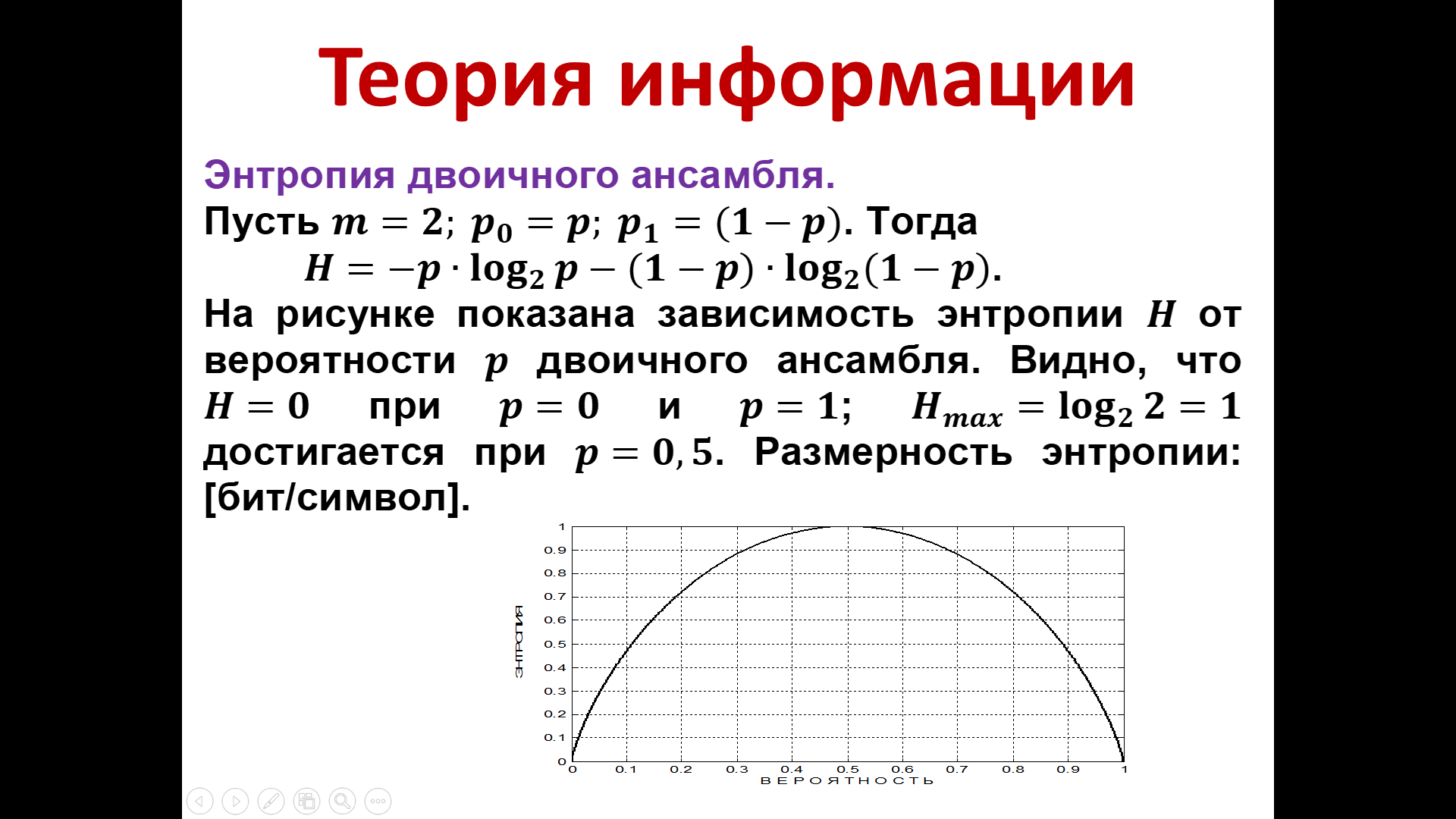
Рисунок 15 – Зависимость энтропии от вероятности двоичного ансамбля
На
рисунке показана зависимость энтропии
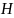 от
вероятности
от
вероятности
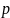 двоичного
ансамбля. Видно, что
двоичного
ансамбля. Видно, что
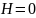 при
при
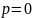 и
и
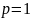 ;
;
 достигается при
достигается при
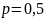 .
Размерность энтропии: [бит/символ].
.
Размерность энтропии: [бит/символ].
Количество информации непрерывных сообщений
Как уже отмечалось, теория информации возникла с целью теоретического рассмотрения того, что происходит в системах связи.
Мы знаем, что все виды сигналов подразделяются на 4 вида - это непрерывный сигнал, непрерывно-дискретный, дискретно-непрерывный и дискретный сигналы или дискретное сообщение.
Обратимся еще раз к дискретным сообщениям или сигналам т.е. к тем, которые принимают значения в дискретные моменты времени из дискретного множества. Пример – буквы русского или латинского алфавита, арабские цифры. Так же сигнал, принимающий те или иные значения напряжения в дискретные моменты времени.
Именно такого рода источники мы рассматривали до сих пор, определяли количество информации, среднее значение количества информации (энтропию) и изучали её свойства.
На рисунке 16 представлены две диаграммы, которые с общих позиций ещё раз поясняют это.
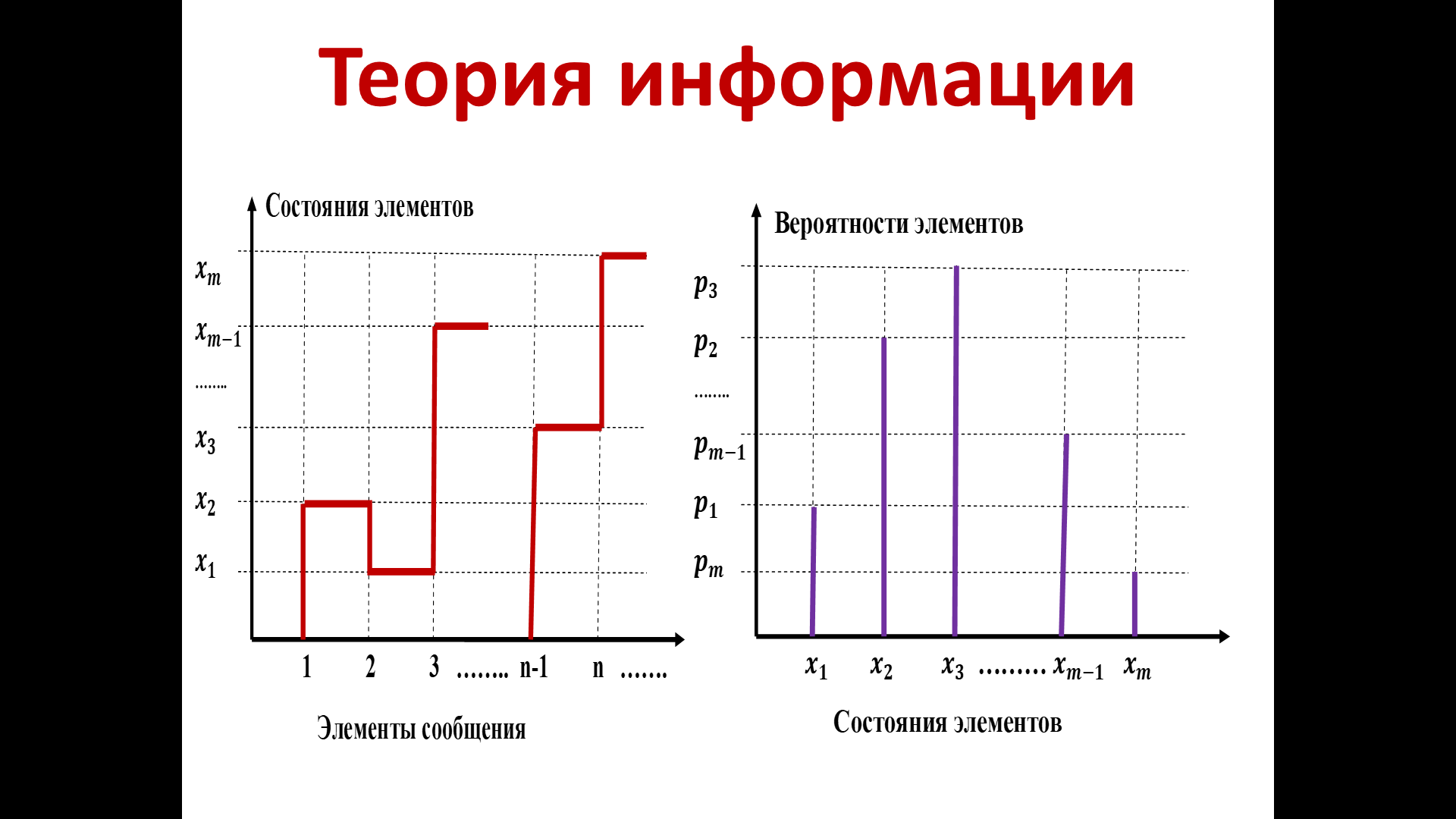
Рисунок 16– Сообщения, вырабатываемые источником
Итак, наш источник вырабатывает сообщения, которые принимают одно из множества значений х1, х2, …хm.
Условимся ранжировать значения этих сигналов, полагая, что x1<x2<…<xm. На самом деле разделение условное, если введена метрика. Элементы сообщений не обязательно принадлежат элементам метрического пространства, они могут быть элементами топологического пространства. Например, если элементы сообщений - буквы.
Мы не можем сказать, что a<b<c, между ними нет таких отношений. Поэтому данный график подойдет для общих рассуждений.
Будем полагать, что элементы дискретных сообщений х1, х2, …хm соответствующим образом заданы, само сообщение формируется в некоторые моменты времени, которые условно обозначим 1,2,…n.
Сообщения формируются в эти моменты времени, принимая значения от х1 до хm, что изображено в виде «скачущей» кривой из одного состояния в другое.
В
данном примере в некоторый 1-ый момент
времени сообщение принимает значение
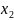 ,
во 2-ой –
,
во 2-ой –
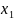 ,
в 3-ий –
,
в 3-ий –
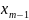 и т.д.
и т.д.
Вторая диаграмма поясняет описание данного источника с позиций теории вероятности, что позволяет оценить количество информации. На этой диаграмме представлено распределение вероятностей появления различных сообщений от источника.
На рис.16 представлен один из вариантов реализации случайного появления сообщений х1, х2, …хm, возникающих от данного источника, и соответствующее распределение вероятностей, которое, в качестве примера, также характерно для данного источника.
Помимо дискретных сигналов существуют непрерывные, непрерывно-дискретные, дискретно-непрерывные. После определения количественных оценок дискретных источников, попробуем разобраться с применением аналогичного подхода для других сигналов.
Пусть сообщение принимает некоторые значения на отрезке от xmin до xmax. В отличие от предыдущего случая, мы не знаем дискретные значения, которые принимает сообщение. У нас нет дискретных букв алфавита, сообщение может принимать любые значения от xmin до xmax. Пример возможной реализация данного сообщения показан на левой диаграмме (рис.17). В 1-ый момент времени сообщение принимает значение х1, во 2-ой - х2 и т.д.
Поскольку источник не дискретный, для вероятностного описания воспользуемся плотностью вероятностей элементов. В качестве примера изображена красная кривая, которая соответствует плотности вероятности элементов данного источника. Эта плотность вероятности имеет вид, отражающий статистические особенности данного источника. Довольно часто в рассматриваемых теоретических моделях – эта плотность имеет характер нормального закона распределения, либо экспоненциального, и проч.
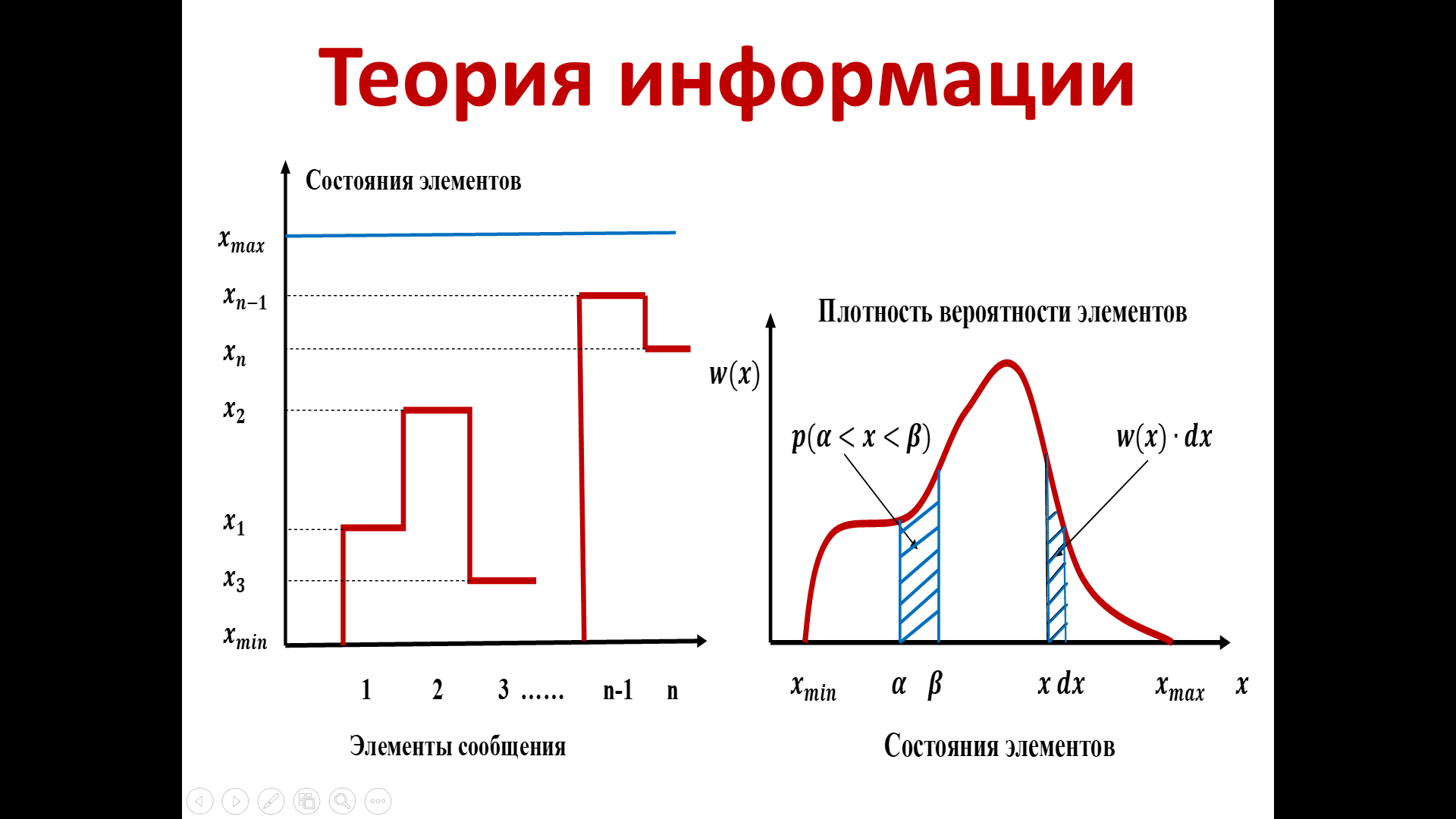
Рисунок 17 – Диаграммы состояния элементов сообщения
(В данном случае мы наугад предположили, что плотность вероятности будет иметь вид как на 2-ой диаграмме рис.17).
Чтобы
оценить вероятность принятия сообщением
значения на интервале от
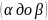 ,
мы можем воспользоваться формулой:
,
мы можем воспользоваться формулой:
 (17)
(17)
Вероятность равна интегралу от плотности вероятности. Устремляя значение интервала к нулю, мы можем оценить соответствующую вероятность.
Для
дискретного источника энтропия как
среднее значение количества информации
определяется по формуле
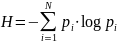 .
Когда
источник перестает быть дискретным,
вероятность можно выразить через
плотность
.
Когда
источник перестает быть дискретным,
вероятность можно выразить через
плотность
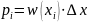 ,
где
,
где
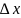 – интервал между
– интервал между
 .
.
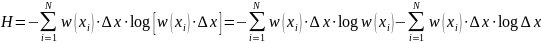 (18)
(18)
Устремляя к 0, мы получаем соответствующую оценку вероятности.
Подставляя данное выражение в вычислении энтропии дискретного источника, мы получим выражение, которое можно разделить на 2 суммы:
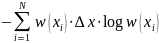 и
и
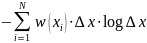 (19)
(19)
При –> 0, первое слагаемое станет
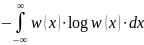 (20)
(20)
Можно сравнить данное выражение с тем, которое было дано для вычисления энтропии дискретного источника и увидеть их схожесть. Отличие в том, что знак суммы теперь «заменен» на знак интеграла.
Второе
слагаемое при
–> 0, с учетом
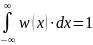 ,
будет равно:
,
будет равно:
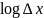 .
(21)
.
(21)
Полученный
результат показывает, что энтропия для
источника, в котором сообщения принимают
не дискретное, а любое значение между
xmin
и xmax,
может быть охарактеризован энтропией,
вычисляемой как сумма двух слагаемых
из (20) и (21), а именно: - и -
.
и -
.
При –> 0, 2-ое слагаемое будет стремиться к бесконечности. Таким образом, энтропия непрерывного источника при –>0, так же стремится к бесконечности.
Но часто этим слагаемым пренебрегают, зафиксировав значение , и, «отбрасывая» данную константу, не зависящую от статистических особенностей источника. Это означает, что при анализе непрерывного источника осуществляется его оценка с точностью .
Когда
эта оценка принята, то непрерывный
источник трансформируется в дискретный
источник с оценкой погрешности
 В
случае, если мы хотим иметь более точное
описание, это будет означать, что
меньше, нам стоит заново оценить энтропию
непрерывного источника.
В
случае, если мы хотим иметь более точное
описание, это будет означать, что
меньше, нам стоит заново оценить энтропию
непрерывного источника.
Мы установили, что у дискретного источника энтропия максимальна, когда вероятности всех сообщений равны между собой и значение энтропии равно логарифму от количества сообщений.
Получим подобные оценки для непрерывного источника.
Предположим, что дисперсия состояний элементов сообщений ограничена, а среднее значение равно 0.
Тогда
при
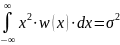 и
рассмотрим
и
рассмотрим
 (22)
(22)
После определенных преобразований по нахождению экстремума, получим выражение, доказывающее, что энтропия в этом случае максимальна при нормальном центрированном распределении плотности, а именно, когда
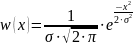 (23)
(23)
Подставив данное выражение в (22) получаем
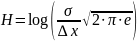 (24)
(24)
Для
сравнения отметим, что для дискретного
источника максимальная энтропия будет
в случае, когда вероятности всех сообщений
равны между собой и, соответственно,
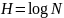 .
Для
непрерывного источника мы установили
другое значение максимальной энтропии
-
при условии, что дисперсия состояния
элементов ограничена, а среднее значение
равно нулю. При этом максимальное
значение энтропии достигается, когда
плотность вероятности распределена по
нормальному центрированному закону.
.
Для
непрерывного источника мы установили
другое значение максимальной энтропии
-
при условии, что дисперсия состояния
элементов ограничена, а среднее значение
равно нулю. При этом максимальное
значение энтропии достигается, когда
плотность вероятности распределена по
нормальному центрированному закону.
Помимо случая, когда дисперсия состояния элементов ограничена, рассмотрим другой случай, когда дисперсия не ограничена. Для непрерывного источника при этом условии и условии нормировки, а именно , значение энтропии будет максимально уже не при нормальном законе распределения, а при равномерном распределении на интервале от a до b.
Плотность распределения в данном случае должна быть равномерной, чтобы энтропия была максимальной и равна
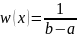 ,
(25)
,
(25)
сама же энтропия
 (26)
(26)
Полученные результаты указывают на максимальное значение энтропии для дискретных и непрерывных источников. При этом видны существенные отличия между ними.
