
- •Введение
- •Информация, сообщения, сигналы
- •Блок-схема передачи информации
- •Краткая история и примеры устройств передачи различных сообщений
- •Классификация сигналов
- •Количество информации дискретных сообщений
- •6.1 Свойства энтропии источника
- •6.1.1 Энтропия максимальна и равна:
- •6.1.2 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.
- •6.1.4 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.
- •6.2 Двоичный дискретный источник
- •Количество информации непрерывных сообщений
- •Статистически зависимые источники сообщений
- •Практические приложения теории информации
- •9.1 Сигнал и аддитивная помеха
- •9.2 Кодирование дискретных сообщений
- •9.3 Эффективное первичное кодирование
- •9.2.1 Метод укрупнения алфавита
- •9.2.2 Методы статистического кодирования
- •9.2.3 Кодирование в биологических структурах
- •Курсовая работа по теории информации
9.2.1 Метод укрупнения алфавита
Пусть 10-ичный источник создает последовательности цифр: ...3, 1, 5, 7, 9, 8, 0, 2, ... и пусть очередная цифра выбирается независимо от предыдущей с одинаковой вероятностью 1/10 (поскольку цифр всего 10).
Если
применять примитивное
двоичное кодирование,
то каждая десятичная цифра заменяется
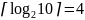 символьной двоичной комбинацией. Для
передачи
символьной двоичной комбинацией. Для
передачи
![]() десятичных цифр придется израсходовать
4
двоичных символов. Однако энтропия
источника ДС в данном случае
десятичных цифр придется израсходовать
4
двоичных символов. Однако энтропия
источника ДС в данном случае
![]() и в соответствии с первой теоремой
Шеннона должен существовать код с
и в соответствии с первой теоремой
Шеннона должен существовать код с
![]() .
Найдем
его, укрупняя
алфавит.
Для этого разобьем
десятичную последовательность на пары
цифр: ...31,
57, З8, 02, 10, 47,11, 25, и каждую пару будем
примитивно кодировать как единый
символ нового,
большего по мощности, алфавита. Поскольку
таких разных пар будет 100, то понадобятся
.
Найдем
его, укрупняя
алфавит.
Для этого разобьем
десятичную последовательность на пары
цифр: ...31,
57, З8, 02, 10, 47,11, 25, и каждую пару будем
примитивно кодировать как единый
символ нового,
большего по мощности, алфавита. Поскольку
таких разных пар будет 100, то понадобятся
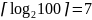 -ми
символьные двоичные кодовые комбинации.
При этом на одну десятичную цифру будет
расходоваться уже 7/2=3.5 двоичных символов.
-ми
символьные двоичные кодовые комбинации.
При этом на одну десятичную цифру будет
расходоваться уже 7/2=3.5 двоичных символов.
Этот процесс можно продолжить и попытаться кодировать тройки десятичных цифр: ...315, 798, 021, 047, 112, 5, ... и т.д. Постепенно мы приблизимся к теоретически достижимому пределу. Однако при этом растет задержка и ухудшается помехоустойчивость.
Действительно, если из-за помех будет искажена кодовая комбинация, кодирующая каждую отдельную цифру, то повреждение коснется только этой цифры. А при кодировании, например, 3-х цифр, повреждения или неверное декодирование кодовой комбинации будет означать повреждение 3-х десятичных цифр.
Помимо метода укрупнения алфавита существует так называемый метод статистического кодирования, учитывающий значения вероятности того или иного сообщения. Разберем это на примере двоичного кодирования.
9.2.2 Методы статистического кодирования
При статистическом двоичном кодировании элементов ДС используются кодовые комбинации разной длины. Причем более вероятным элементам ДС, приписываются более короткие кодовые комбинации.
Попутно заметим, что в свое время известному создателю первых телеграфных аппаратов -господину Морзе пришла в голову эта мысль. Азбука Морзе является примером статистического кодирования, при котором буквам латинского алфавита (в последующем русского алфавита) присваивались наиболее короткие комбинации в виде точек и тире.
Наибольшее снижение избыточности достигается кодированием по методу Фано-Шеннона или Хаффмана. Рассмотрим пример построения неравномерного кода по методу Хаффмана, имеющего более общий алгоритм.
Поясним
на примере двоичного кодирования
(ансамбля
![]() ,
характеризуемого 8-ью сообщениями
,
характеризуемого 8-ью сообщениями
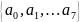 и соответственно вероятностями их
появления
и соответственно вероятностями их
появления
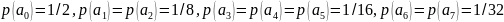 .
Пример наглядно изображен на рисунке
27.
.
Пример наглядно изображен на рисунке
27.

Рисунок 22 – Алгоритм Хаффмана
На 1-ом этапе объединяются два наименее вероятных события в одно составное (с суммарной вероятностью объединяемых событий), в нашем примере
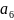 и
и
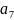 с суммарной вероятностью 1/32 + 1/32 = 1/16;
с суммарной вероятностью 1/32 + 1/32 = 1/16;На 2-ом и последующих этапах процедура 1-го этапа повторяется до тех пор, пока суммарная вероятность составного события не достигнет единицы. При этом не важно какие события объединяются при равенстве вероятностей. Выбор произволен. Основное и единственное требование - это чтобы объединяемые события имели наименьшие вероятности;
После достижения суммарной вероятности окончательного составного события равной единице, осуществляется кодирование, начиная с конечного узла, имеющего вероятность 1. Предварительно установив правило кодирования (стрелка вверх – это 1, а стрелка вниз – это 0), рассматривают «движение» от окончательного составного события к исходным. Например, из рис.22 следует, что для достижения
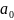 надо совершить одно движение вверх,
что соответствует кодовой комбинации
из одного символа, равного 1. Для
достижения
надо совершить одно движение вверх,
что соответствует кодовой комбинации
из одного символа, равного 1. Для
достижения
 надо «пройти» три стрелочки вниз, что
соответствует комбинации 000 и т.д.
надо «пройти» три стрелочки вниз, что
соответствует комбинации 000 и т.д.
Разберем
подробнее пример построения для
заявленного на рис.22 источника с восемью
сообщениями. Будем использовать
табличную форму построения, запишем
все сообщения дискретного источника
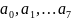 ,
рядом запишем вероятности этих сообщений.
,
рядом запишем вероятности этих сообщений.
Следуя алгоритму, предложенному Хаффманом, на первом этапе мы должны объединить и , при этом объединённое состояние будет иметь сумму их вероятностей и будет равно 1/16.
На
следующем шаге мы вольны в выборе
(вероятности равны). Продолжаем и соединим
объединённое состояние
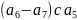 .
.
На
следующем шаге наша объединение очевидно
- это объединение сообщений
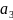 и
и
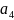 . После объединения возникает четыре
состояния с равными вероятностями 1/8.
Мы делаем свой выбор, хотя возможны и
другие варианты.
. После объединения возникает четыре
состояния с равными вероятностями 1/8.
Мы делаем свой выбор, хотя возможны и
другие варианты.
Следующий
шаг очевиден - это объединение
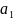 и
. Следующий за ним шаг тоже достаточно
понятен, объединение соответствующих
состояний с вероятностью 1/4. Наконец,
на последнем шаге мы объединяем составные
состояния с сообщением
,
имеющим вероятность 1/2. В итоге получаем
финальное значение вероятности, равное
единице.
и
. Следующий за ним шаг тоже достаточно
понятен, объединение соответствующих
состояний с вероятностью 1/4. Наконец,
на последнем шаге мы объединяем составные
состояния с сообщением
,
имеющим вероятность 1/2. В итоге получаем
финальное значение вероятности, равное
единице.
После этого мы устанавливаем, что движение по графу вверх будет соответствовать единице, движение вниз будет соответствовать нулю. (Возможна и противоположная договоренность). Двигаясь в обратном направлении, мы легко замечаем, что сообщению будет соответствовать кодовая комбинация 1, сообщению - 001 для, движение показывает, что кодовая комбинация равна 000. Действительно, из узла графа мы трижды идём вниз, что соответствует трем нулям. Ровно также двигаясь по этому графу, мы устанавливаем кодовые комбинации для всех 8 сообщений при кодировании статистическим кодом по алгоритму Хаффмана.
Можно отметить, что неравномерный код обладает лучшей скоростью кодирования, но имеет худшую помехоустойчивость по сравнению с равномерным кодом, а также более сложную реализацию. Следует также отметить неравномерность задержки, что также усложняет восстановление исходного сообщения.
Для того, чтобы определить среднее количество символов, приходящихся на одно сообщение, для данного распределения найдем математическое ожидание (с учётом того, что кодовая комбинация длиной в один символ возникает с вероятно 1/2, кодовая комбинация из 3-х символов возникает с вероятностью 1/8 и т.д. ).
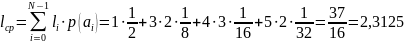
При равномерном кодировании каждая кодовая комбинация кодируется тремя символами. В таблице 1 представлена таблица, которая соответствует кодированию сообщений кодом Хаффмана и некоторым первичным (часто говорят натуральным) кодом.
Таблица 6
Сообщ. |
|
|
|
|
|
|
|
|
Хаффм |
1 |
001 |
000 |
0101 |
0100 |
0111 |
01101 |
01100 |
Натур. |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
Если мы попробуем декодировать некоторую случайную последовательность нулей и единиц, показанную в таблице, то по Хаффману нам удастся идентифицировать эту двоичную последовательность.
Декодируем последовательность:
…01001111001001010101010001110110110110011010000010010100…
По Хаффману:
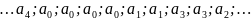
Этот пример говорит о том, что код Хаффмана обладает самосинхронизирующим свойством, это префиксный код, в котором начало каждой кодовой комбинат индивидуально и не совпадает с началами других кодовых комбинаций. Этого свойства нет у натурального (или взвешенного) кода. Для того чтобы обеспечить декодирование необходимо решить задачу синхронизации.
Натуральный (взвешенный) код:
- необходимо обеспечить обнаружение начало кодовых комбинаций и только потом декодирование:
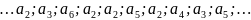
Неравенство
Крафта-Макмиллана устанавливает, что
при заданных кодируемом и кодирующем
алфавитах, состоящих соответственно
из
n
и d
символов, а так же заданных желаемых
длин кодовых слов:
![]() ,
необходимым и достаточным условием
существования разделимого и префиксного
кодов, обладающих заданным набором длин
кодовых слов является выполнение
неравенства:
,
необходимым и достаточным условием
существования разделимого и префиксного
кодов, обладающих заданным набором длин
кодовых слов является выполнение
неравенства:
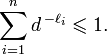 (57)
(57)

