6.1 Свойства энтропии источника

6.1.1 Энтропия максимальна и равна:

Для доказательства этого воспользуемся методом неопределенных множителей Лагранжа. С учетом условия нормировки, ког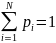да и, полагая , найдем экстремум функционала следующего вида:

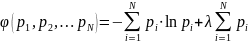(7)

Дифференцируя по , и приравнивая производные нулю, получаем

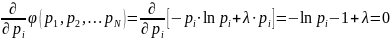(8)

Отсюда следует, что 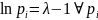и не зависит от номера 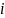, что может быть только при равенстве всех 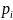, а значит .

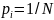Подставляя эту величину, вычислим:

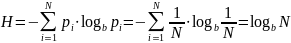(9)

Утверждение 6.1.1 доказано!

6.1.2 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.

Первые два утверждения следуют из определения энтропии и очевидного неравенства:

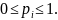
Для доказательства третьего рассмотрим слагаемое 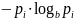. При 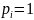результат очевиден. При 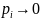имеем 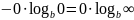. Раскроем неопределенность по правилу Лопиталя, положив :

(10)

Утверждение 6.1.2 доказано!

6.1.3 Энтропия максимальна и равна: H_max = log_b N

Для доказательства этого воспользуемся методом неопределенных множителей Лагранжа.

С учетом условия нормировки, когда , и, полагая b = e, найдем экстремум функционала следующего вида:

(11)

Фактически, мы должны найти значение лямбда, при котором определенный функционал будет иметь точку экстремума.

Дифференцируя по p_i, и приравнивая производные к нулю, получаем:

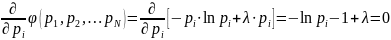(12)

Отсюда следует, что и не зависит от номера i, что может быть только при равенстве всех p_i, а значит p_i = 1/N.

Подставляя эту величину, вычислим:

(13)

Энтропия как среднее значение количества информации будет равна данному выражению.

Мы доказали, что энтропия максимальна в том случае, когда все события равновероятны и при этом энтропия равна логарифму от числа всех возможных сообщений.

6.1.4 Энтропия есть величина вещественная и неотрицательная, а так же ограниченная.

Первые два утверждения следуют из определения энтропии как среднего значения и очевидного неравенства: 0 ≤ p_i ≤ 1.

Для доказательства третьего рассмотрим слагаемое – p_i ∙ log_b p_i

При p_i = 1 результат очевиден и равен 0.

При p_i → 0 имеем: – 0 ∙ log_b 0=0 ∙ log_b ∞

Получаем неопределенность и запишем с изменением знака данное выражение.

Раскроем неопределенность по правилу Лопиталя, положив b = e:

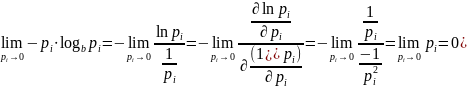(14)

Согласно правилу Лопиталя, для нахождения предела переходим к рассмотрению отношения предела первых производных. После преобразований убеждаемся, что и в этом случае значение энтропии равно нулю.

Таким образом, имеем важные характеристики для энтропии, а именно, энтропия вещественна, неотрицательна, ограничена.

Исследуя свойства энтропии, интересно рассмотреть, как ведут себя элементы, входящие в состав суммы, определяющей энтропию. А именно как ведет себя выражение

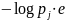
6.1.5 Докажем, что величина (– p_j ∙ log p_j) принимает максимальное значение при p_j = e ^{– 1}

Доказательство простое - возьмем производную от этого выражения и приравняем к нулю.

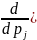(15)

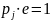Вывод: и, следовательно, p_j = e ^{– 1}

Для наглядности построим график зависимости этого произведения(– p_j ∙ log p_j) от .

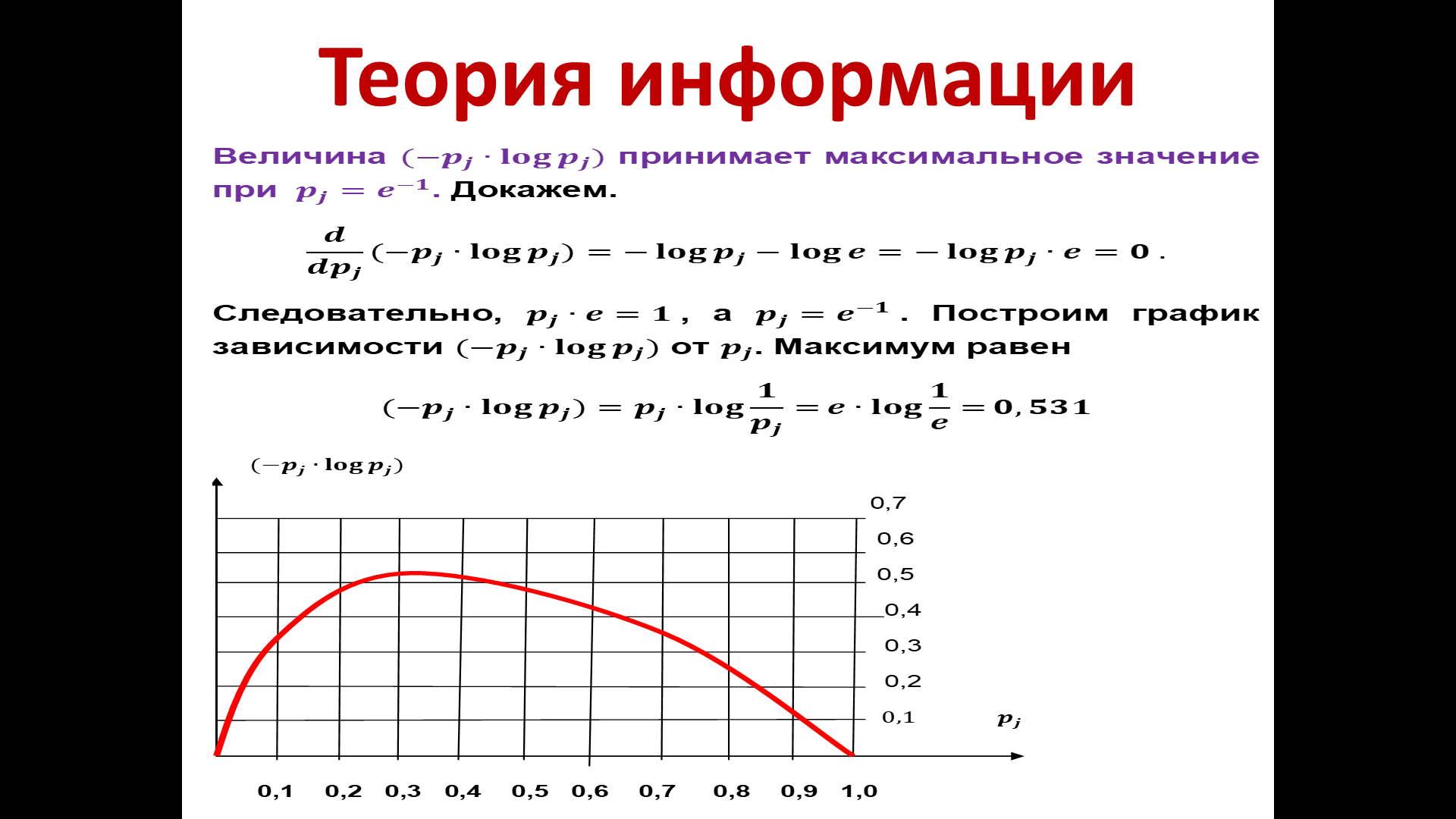
Рисунок 14 - График зависимости произведения (– p_j ∙ log p_j) от .

Свой максимум выражение достигает при p_j = e ^{– 1}

Максимум равен:

Данные исследования интересны тем, что изучая источники сообщений, мы понимаем, при каких условиях получаем определенные значения энтропии и при каких условиях она максимальна.