10. Курсовая работа по теории информации

Задание на курсовую работу:

1. Построить код Хаффмана для букв русского алфавита.

2. Выбрав ключи, закодировать фамилию, имя и отчество кодом Цезаря и далее, используя «квадрат» Виженера.

3. Используя код п.1 закодировать свои фамилию, имя и отчество, полученные из п.2.

4. Для двух заданных источников дискретных сообщений рассчитать энтропию объединения. (Индивидуальное задание по номеру в журнале).

В процессе изучения курса теории информации предстоит выполнить курсовую работу. Это работа будет состоять из следующих основных разделов:

1. Необходимо построить код Хаффмана для букв русского алфавита, исходя из заданной на семинаре статистики букв русского алфавита. После того, как будет построен код Хаффмана, будет понятно, каким кодом кодируется каждая буква (в том числе пробел).

2. Необходимо применить различные способы шифрования. Каждый студент должен, взяв свою фамилию, имя и отчество, закодировать их кодом Цезаря, выбрав по своему желанию соответствующий ключ. Далее, применив квадрат Виженера, закодированную кодом Цезаря последовательность подвергнуть второму этапу шифрования. При этом каждый студент вправе выбрать удобный для него ключ для квадрата Виженера.

3. Используя код, который был получен после построения кода Хаффмана, закодированные фамилия, имя и отчество кодом Цезаря и с помощью квадрата Виженера, следует представить в виде двоичный цифровой последовательности применив код Хаффмана.

Таким образом, необходимо решить три задачи кодирования. Первым применяется шифрование кодом Цезаря. Далее, используя квадрат Виженера. И, наконец, трансформация фамилии, имени и отчества, зашифрованных двумя способами в двоичную последовательность через код Хаффмана.

4. Завершающим разделом курсовой работы является расчёт энтропии объединения для двух заданных источников дискретных сообщений. Каждый студент берет свое индивидуальное задание по номеру в журнале и проводит расчёт объединения.

Все полученные результаты отражаются в отчете по курсовой работе.

В таблице 9 представлены исходные данные, которые потребуются каждому студенту для расчёта соответствующие энтропии. Например, студент выбирает цифру по номеру журнала. В левом столбике указаны номера с 1 по 32, выберем номер 12. По соответствующей строчки мы видим вероятности четырёх возможных сообщений X₁, X₂, X₃, X₄ равны соответственно 0.125, 0.125, 0.25 и 0.5. Матрица условных вероятностей для всех студентов будет одинаковый. Эта матрица представлена в виде таблицы 8.

Таблица 8

Помимо выполнения расчётных работ, связанных с построением кода, шифрования, расчёта энтропии, каждый студент должен подготовить реферат на одну из тем:

1. История возникновения и развития информационных устройств.

2. История и современность в первичных способах кодирования сообщений.

3. Аналого-цифровые методы преобразований сигналов.

4. Информатизация современного общества.

5. Информационная безопасность, проблемы и пути решения.

6. Информационные технологии в медицине.

7. Информационные технологии в образовании.

Темы в принципе могут быть и другие, но основная направленность должна быть связана с информационными технологиями, с теорией информации.

Таблица 8

Отчет по курсовой работе рекомендуется оформить так, как показано на рисунке 25.

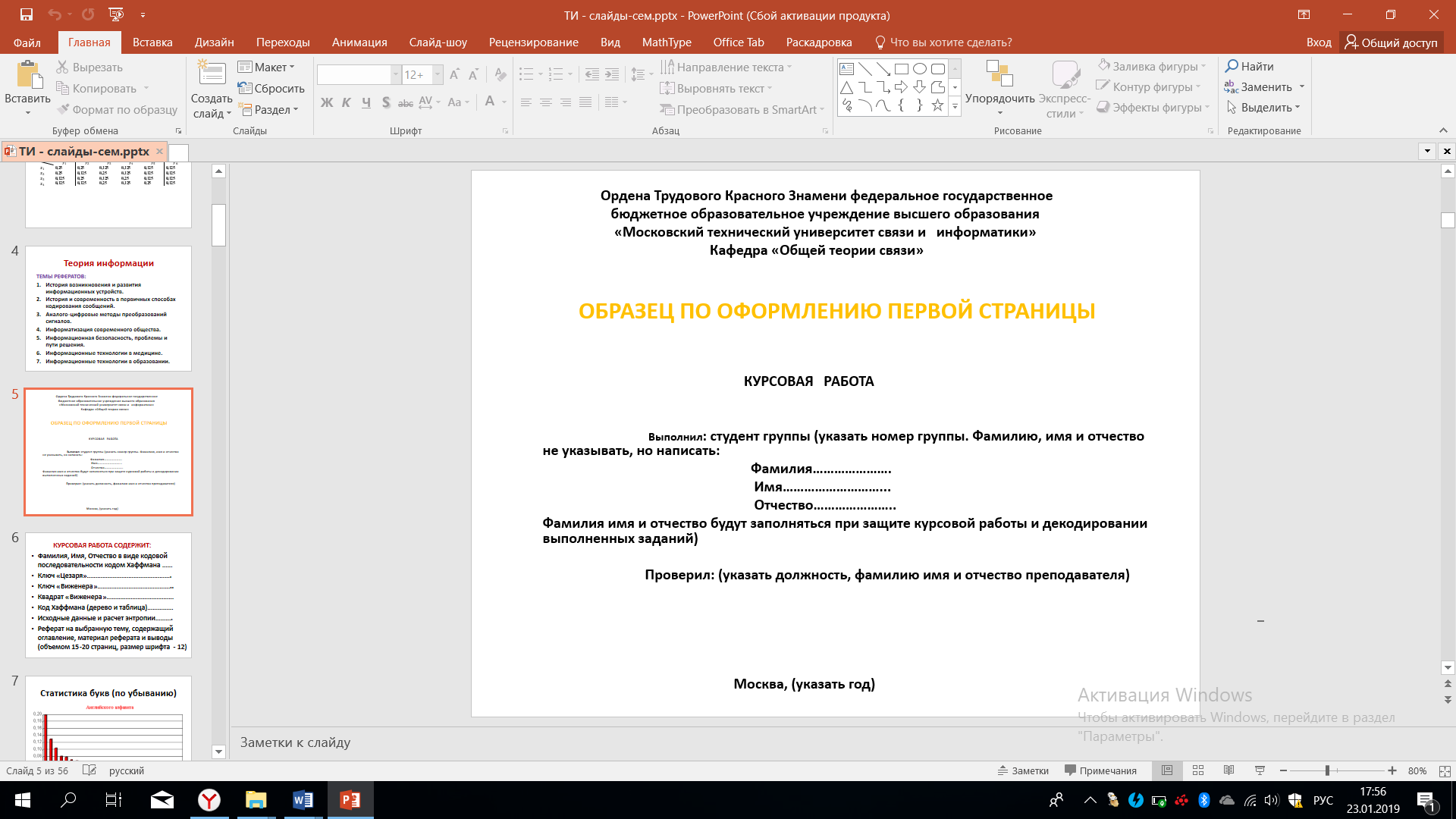
Рисунок 25 – Пример оформления КР

При этом надо обратить внимание на то, что фамилия, имя и отчество на титульном листе не указываются. Фамилия, имя и отчество будут восстановлены или обнаружены при защите курсовой работы. Когда зашифрованные фамилия, имя, отчество кодом Цезаря, с помощью матрицы Виженера и кода Хаффмана будут закодированы, во время защиты работы при условии успешного декодирования можно будет считать, что студент добросовестно выполнил курсовую работу.

В самой курсовой работе должны содержаться следующие сведения: фамилия, имя и отчество в виде кодовой двоичной последовательности, закодированной кодом Хаффмана, должен быть представлен ключ Цезаря и ключ Виженера, а также должен быть приведен квадрат Виженера, дерево кода Хаффмана и соответствующие таблицы, в соответствии с которой проводилась кодирование, в соответствии с которой при защите фамилия, имя и отчество, представленные двоичной последовательностью, будут декодированы. Помимо этого, следует указать исходные данные и расчет энтропии, исходя индивидуального задания по значению вероятности тех или иных сообщений, которые выбираются по номеру журнала.

К рассчитанным данным должен быть приложен реферат на выбранную тему, содержащий оглавление, материал реферата и выводы. Объём реферата 15-20 страниц 14 –м размером шрифта.

При практических занятиях, связанных с изучением статистики дискретных сообщений, следует ознакомиться со статистикой английского алфавита.

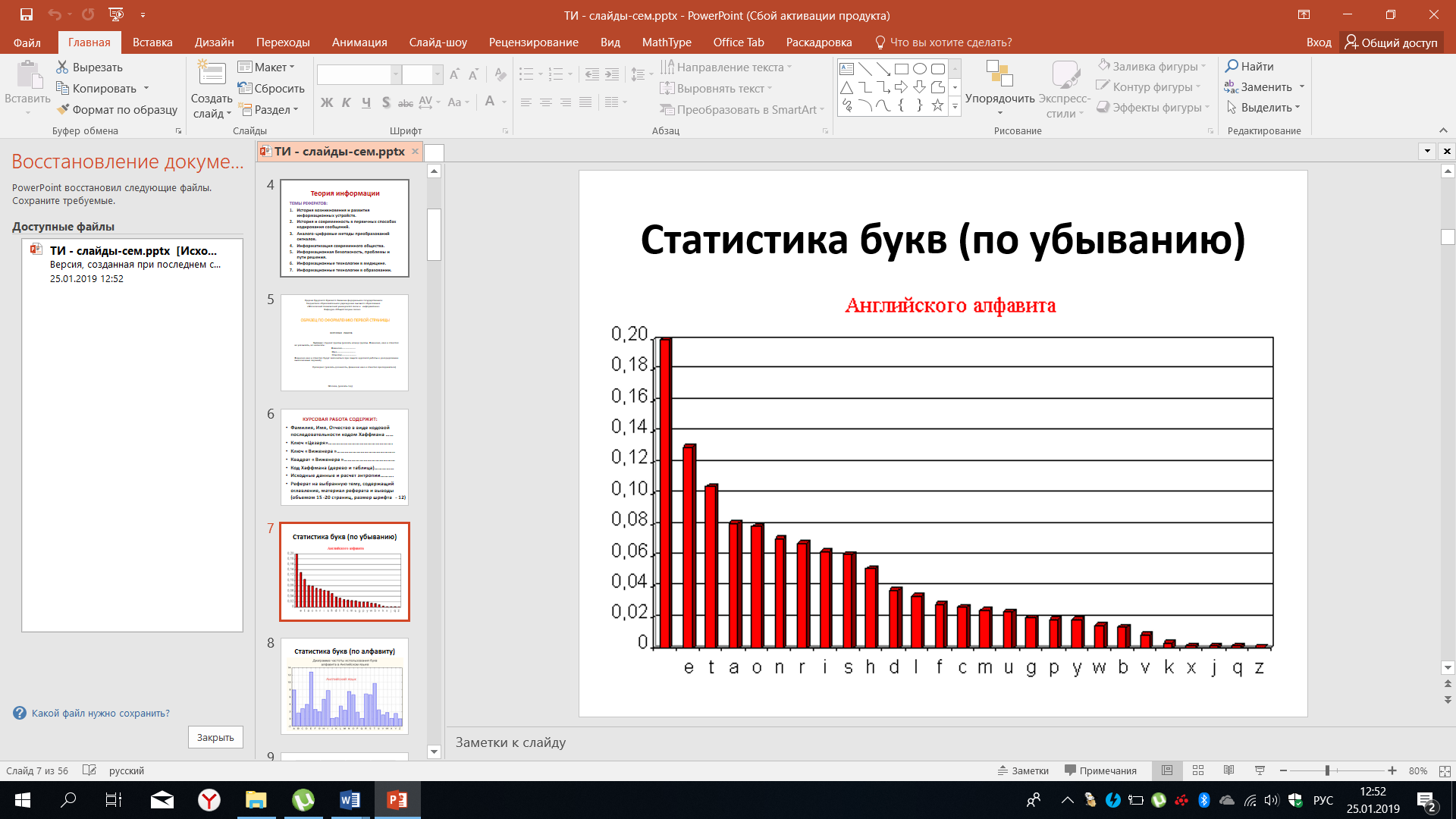
Рисунок 26 – Статистика букв английского алфавита

В данном случае все буквы и пробел, имеющий максимальное значение вероятности появления в речи, представлены в порядке убывания. Эти же данные можно изобразить в последовательности принятых алфавитом, что показано на рисунке 27.

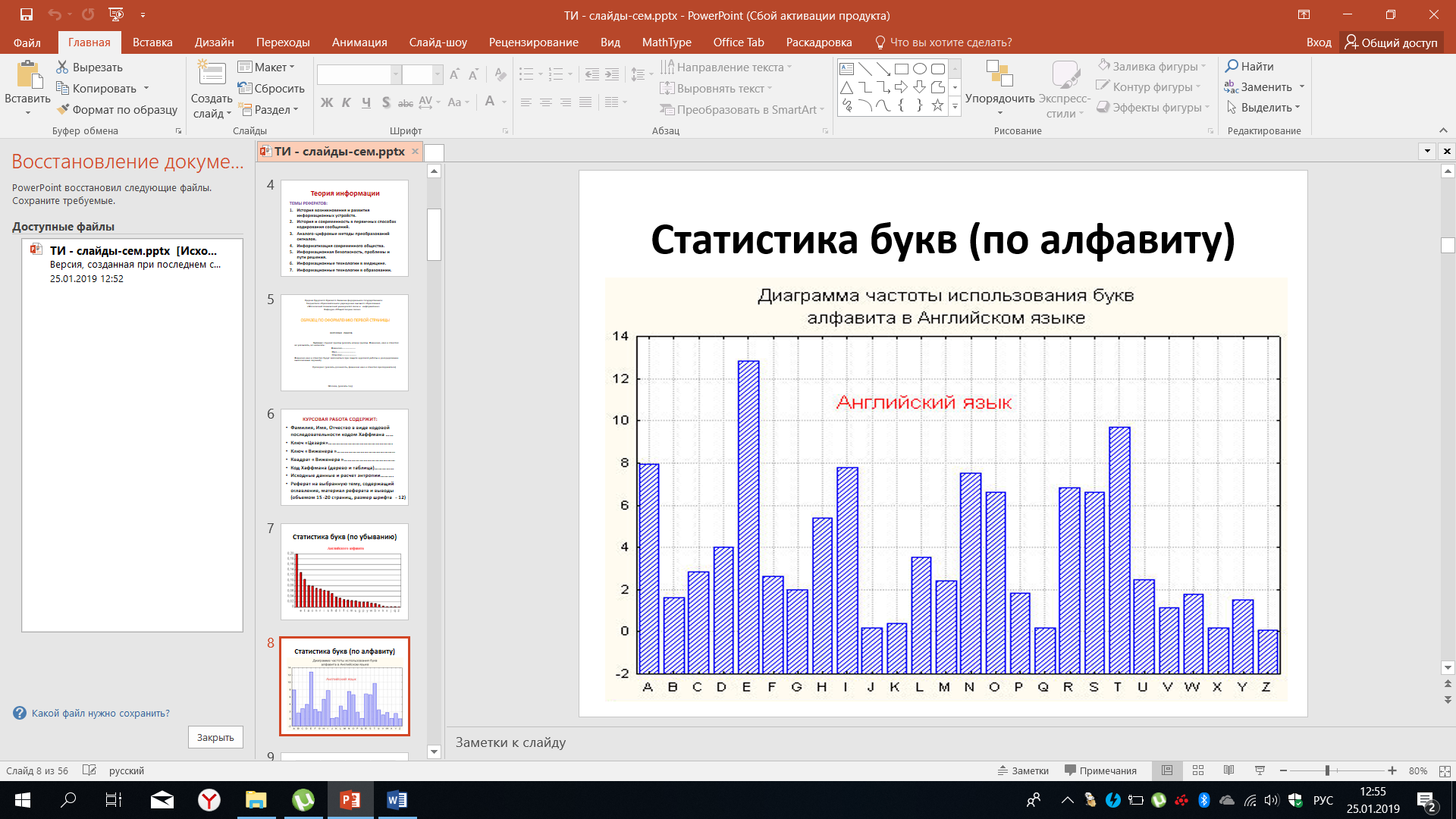
Рисунок 27 – Частота использования букв английского алфавита

Мы видим определённую хаотичность частоты встречаемости тех или иных букв, если их упорядочить в алфавитном порядке. Для проведения расчётов удобно пользоваться таблицей 9, в которой указана частота встречаемости. В таблицу включён и пробел.

Таблица 9 – Встречаемость букв английского алфавита

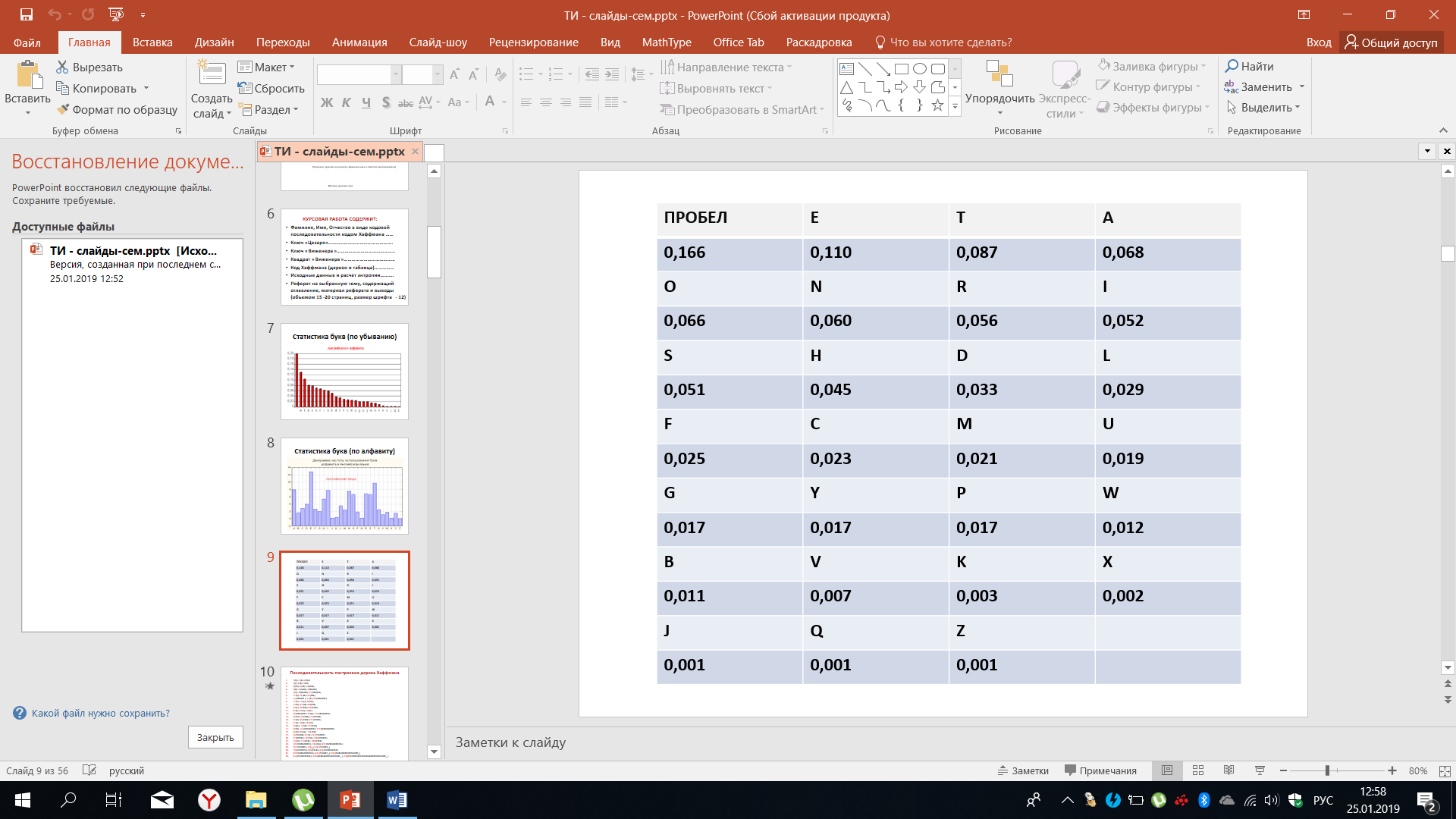
В определённом смысле эти частоты можно рассматривать как оценку вероятности появления букв в различных текстах. Хотя если более строго подходить к этому вопросу, то станет ясно, что вероятности зависит от типа текстов. Тексты могут существенно отличаться, особенно если рассматривать специальные тексты, например, технического плана или медицинского по сравнению с традиционной литературой или с газетной прессой. В этом случае статистика будет разной, что говорит о достаточно сложном анализе, который необходимо провести, чтобы описать источник дискретных сообщений, вырабатывающий буквы и знаки латинского алфавита.

Запишем последовательность построения дерева Хаффмана для букв латинского алфавита:

1. 1(Q)+1(Z)=2(QZ)

2. 1(J)+2(X)=3(JX)

3. 2(QZ)+3(JX)=5(QZJX)

4. 3(K)+5(QZJX)=8(KQZJX)

5. 7(V)+8(KQZJX)=15(VKQZJX)

6. 11(B)+12(W)=23(BW)

7. 15(VKQZJX )+17(P)=32(VKQZJXP)

8. 17(Y)+17(G)=34(YG)

9. 19(U)+21(M)=40(UM)

10. 23(C)+23(BW)=46(CBW)

11. 25(F)+29(L)=54(FL)

12. 32(VKQZJXP)+33(D)= 65(VKQZJXPD)

13. 34(YG)+40(UM)=74(YGUM)

14. 45(H)+46(CBW)=91(HCBW)

15. 51(S)+52(I)=103(SI)

16. 54(FL)+ 56(R)=110(FLR)

17. 60(N)+ 65(VKQZJXPD)=125(NVKQZJXPD)

18. 66(O)+68(A)= 134(OA)

19. 74(YGUM)+87(T)=161(YGUMT)

20. 91(HCBW)+103(SI)=194(HCBWSI)

21. 110(E)+110(FLR)= 220(EFLR)

22. 125(NVKQZJXPD)+134(OA)=259(NVKQZJXPDOA)

23. 161(YGUMT)+166(_)=327(YGUMT_)

24. 194(HCBWSI)+220(EFLR)=414(HCBWSIEFLR)

25. 259(NVKQZJXPDOA)+327(YGUMT_)=586(NVKQZJXPDOAYGUMT_)

26. 414(HCBWSIEFLR)+586(NVKQZJXPDOAYGUMT_)=1000(HCBWSIEFLRNVKQZJXPDOAYGUMT_)

В данном случае реализуется общее правило о том, что события, имеющие наименьшую вероятность встречаемости, объединяются. Этот процесс продолжается до того момента, пока не будут объединены все сообщения, все буквы латинского алфавита.

На рисунке 28 размещены сообщения в порядке убывания их вероятностей, наиболее часто встречается пробел, далее буквы E, T и т.д.

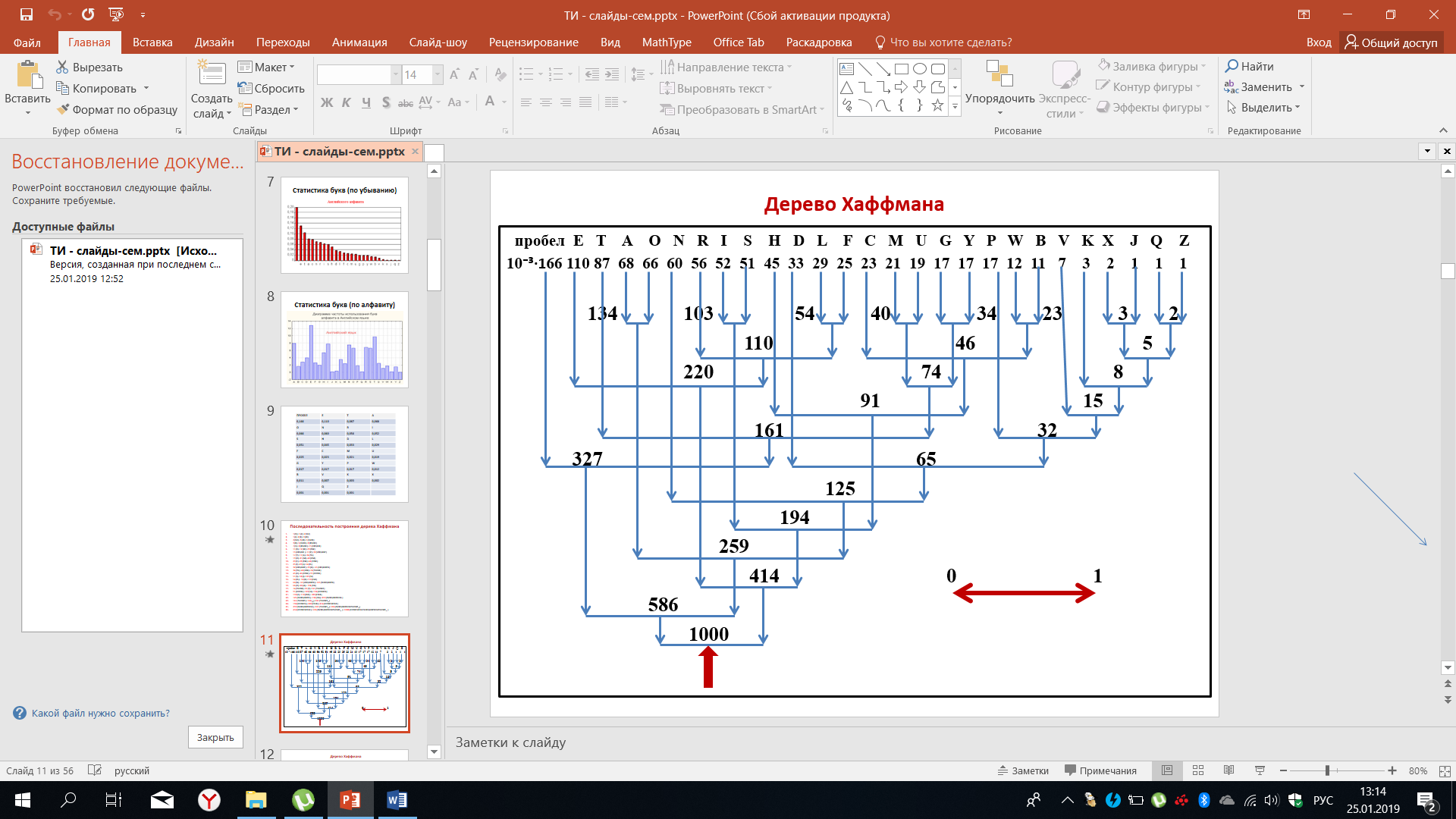
Рисунок 28 – Дерево Хаффмана

На данном рисунке представлена последовательность построения графа или дерево Хаффмана - это дерево в данном случае полностью соответствует той последовательности, которая была приведена на предыдущем рисунке. После того, как построение дерева будет завершено, мы договариваемся о движении в обратном порядке от корня дерева к ветвям, то есть снизу-вверх. В данном случае движение влево соответствует коду 0, движение вправо соответствует 1. В принципе можно принять противоположное решение, но для данного примера мы выберем этот конкретный случай. Рисунок 29 демонстрирует движение от корня к ветвям.

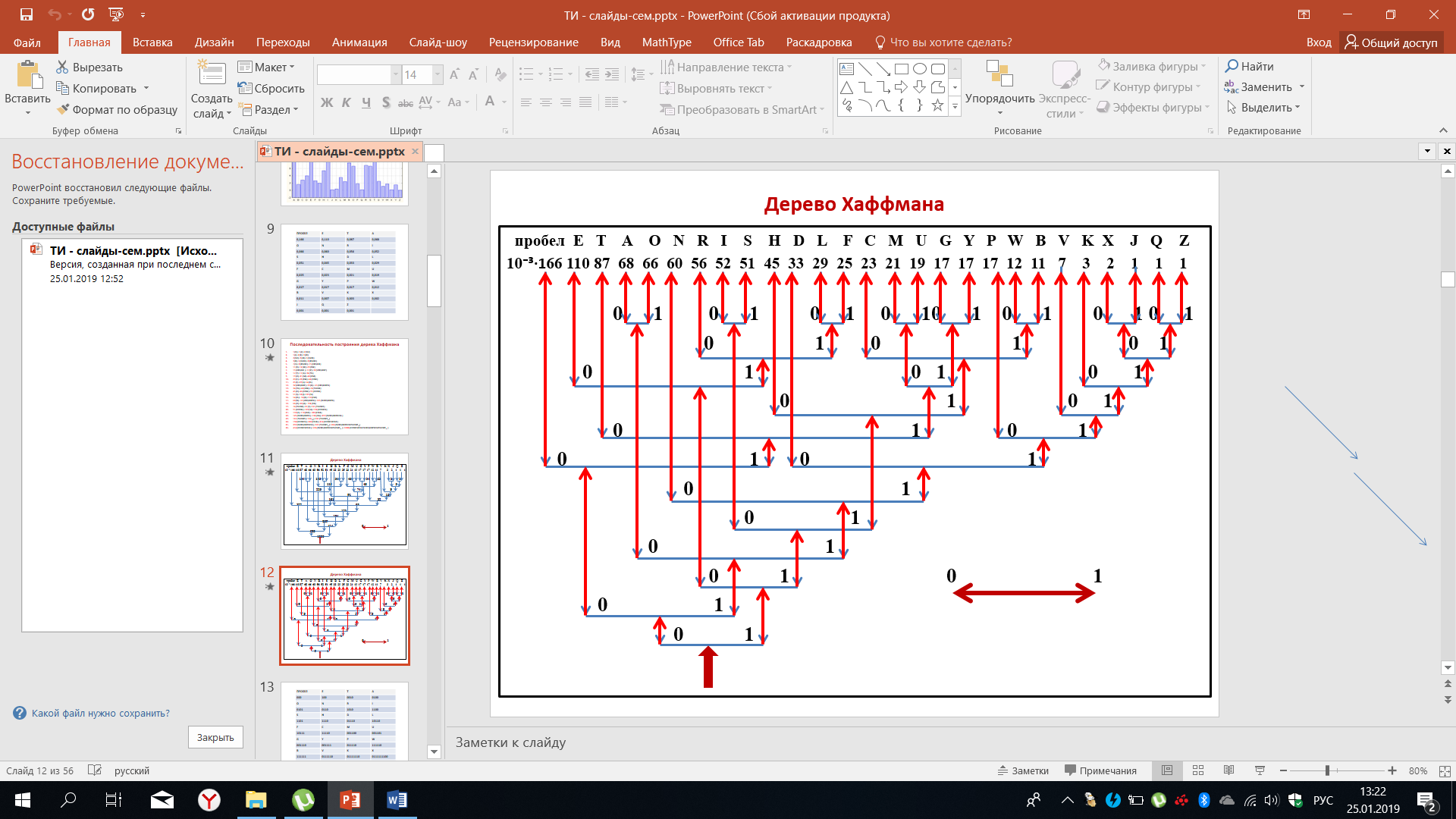
Рисунок 29 – Алгоритм кодирования по Хаффману

Согласно принятой договорённости, когда движение влево соответствует 0, а движение вправо соответствует 1, двигаясь от корня к ветвям дерева Хаффмана, шаги заменяются на соответствующие линии, которые направлены от корня к ветвям, как бы демонстрируя формирование кодовых комбинаций. По завершению мы с вами видим, что, например, пробел кодируется как 000, а буква Е будет закодирована как 100 и т.д.

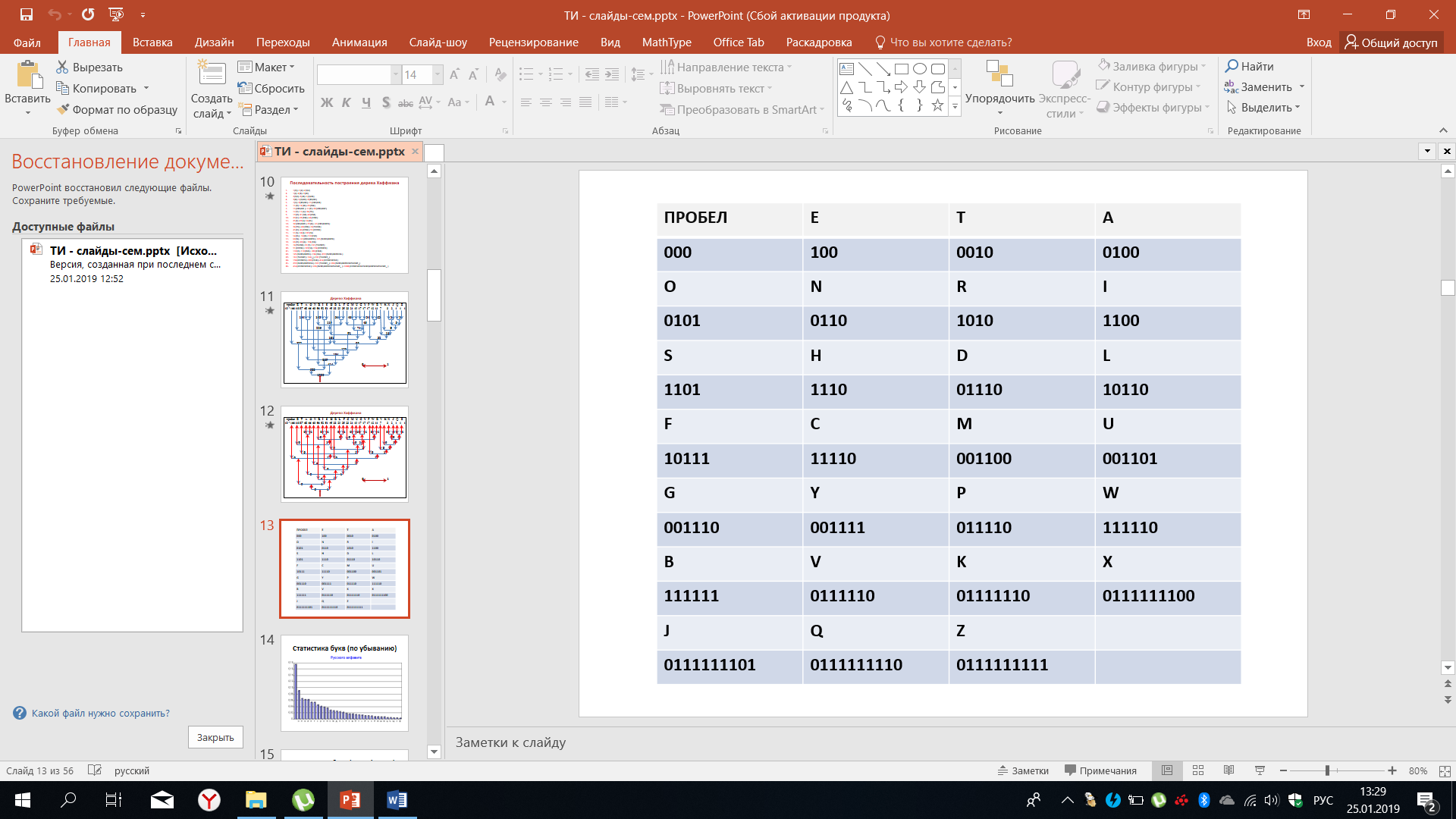
Кодовые слова, отображающие буквы латинского алфавита и пробел, сведены в таблицу 10 для того, чтобы можно было ими пользоваться для кодирования. Итак, из дерева Хаффмана мы получаем кодовые слова.

На рисунке 30 представлена статистика букв по убыванию для русского алфавита. Здесь также дополнительная включён пробел.

Таблица 10 – Кодировка латинского алфавита по Хаффману

Если вспомнить статистику букв латинского алфавита, то можно отметить определённую схожесть, но и некоторые отличия, выраженные в частоте встречаемости тех или иных букв.

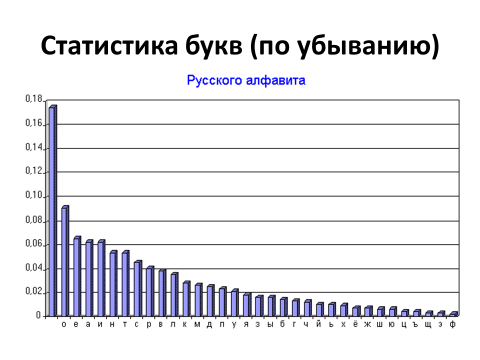
Рисунок 30 – Статистика букв русского алфавита

На рисунке 31 частота использования букв приведена в порядке алфавита для русского языка и, как уже отмечалось, некоторая хаотичность в отдельных случаях используется при реализации тех или иных решений. На самом деле и то, и другое следует изображать в зависимости от тех целей, которые ставятся при анализе статистики.

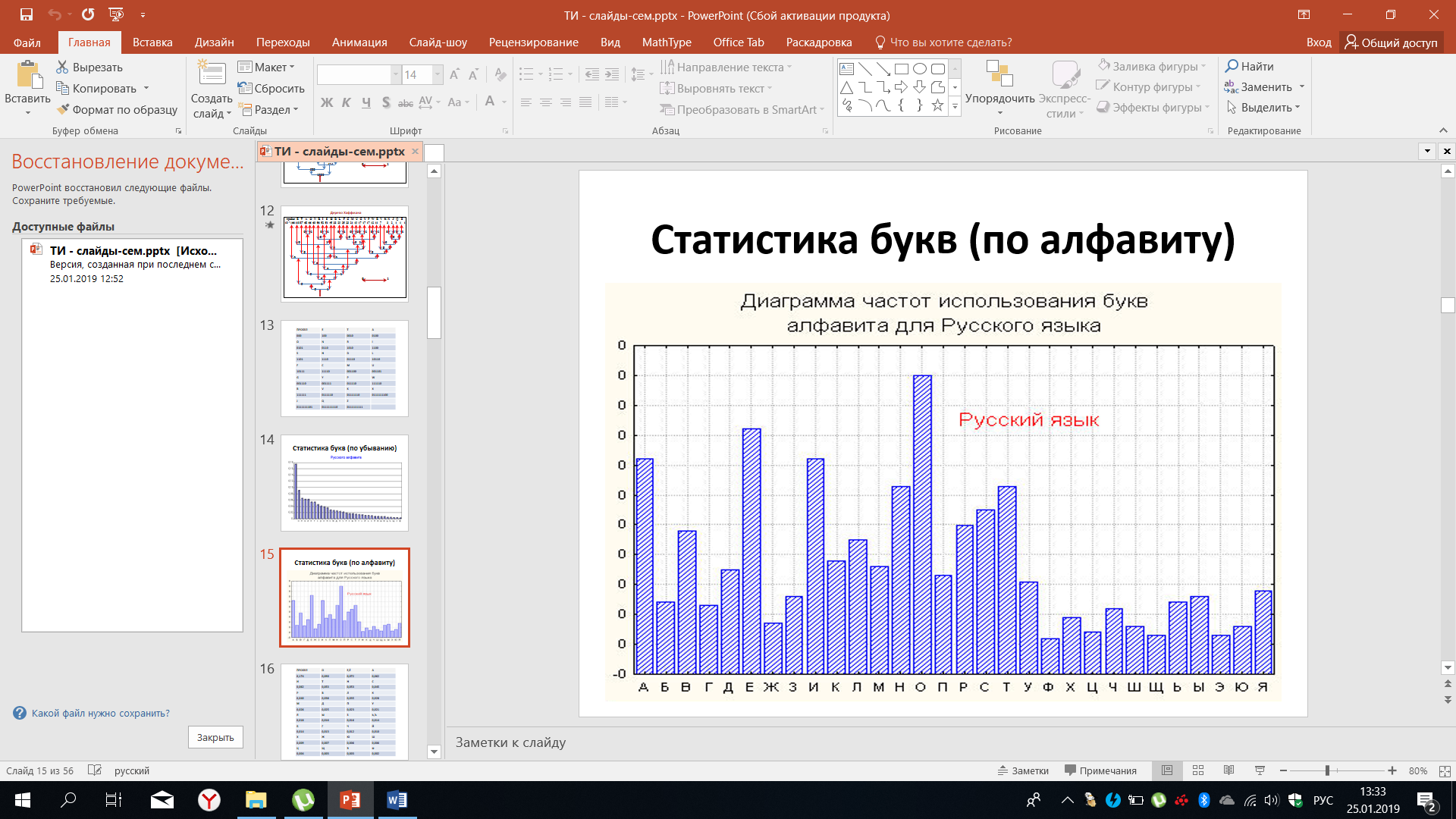
Рисунок 31 – Частота использования букв алфавита для русского языка

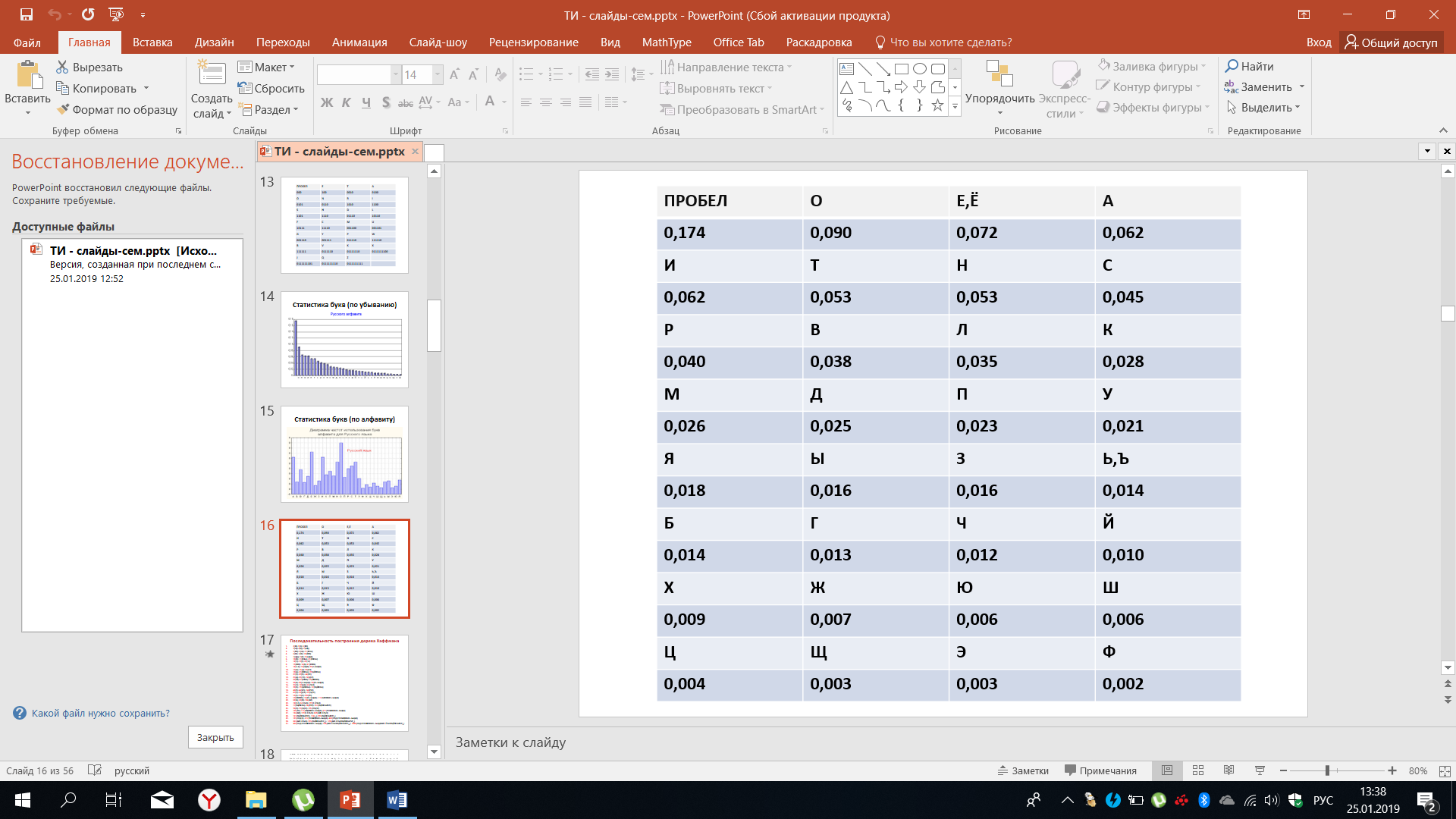
В таблице 11 приведены количественные данные по частоте встречаемости тех или иных букв русского алфавита. Благодаря этой таблице можно построить дерево Хаффмана, последовательно объединяя состояния, объединяя различные буквы, имеющие наименьшие вероятности.

Таблица 11 – Частота встречаемости букв русского алфавита

Запишем последовательность построения дерева Хаффмана, а точнее последовательность объединения различных состояний, что мы будем использовать при построении дерева:

1. 2(Ф)+3(Э)=5(ФЭ)

2. 3(Щ)+4(Ц)=7(ЩЦ)

3. 5(ФЭ)+6(Ш)=11(ФЭШ)

4. 6(Ю)+7(Ж)=13(ЮЖ)

5. 7(ЩЦ)+9(Х)=16(ЩЦХ)

6. 10(Й)+11(ФЭШ)=21(ЙФЭШ)

7. 12(Ч)+13(Г)=25(ЧГ)

8. 13(ЮЖ)+14(Б)=27(ЮЖБ)

9. 14(Ъ-Ь)+16(ЩЦХ)=30(Ъ-ЬЩЦХ)

10. 16(Ы)+16(З)=32(ЫЗ)

11. 18(Ц)+21(ЙФЭШ)=39(ЦЙФЭШ)

12. 21(У)+23(П)= 44(УП)

13. 25(Д)+25(ЧГ)= 50(ДЧГ)

14. 26(М)+27(ЮЖБ)=53(МЮЖБ)

15. 28(К)+30(Ъ-ЬЩЦХ)=58(КЪ-ЬЩЦХ)

16. 35(Л)+ 32(ЫЗ)=67(ЛЫЗ)

17. 38(В)+ 39(ЦЙФЭШ)=77(ВЦЙФЭШ)

18. 40(Р)+44(УП)= 84(РУП)

19. 45(С)+50(ДЧГ)=95(СДЧГ)

20. 53(Т)+53(Н)=106(ТН)

21. 53(МЮЖБ)+58(КЪ-ЬЩЦХ)= 111(МЮЖБКЪ-ЬЩЦХ)

22. 62(А)+62(И)=124(АИ)

23. 72(Е-Ё)+67(ЛЫЗ)=139(Е-ЁЛЫЗ)

24. 77(ВЦЙФЭШ)+84(РУП)=161(ВЦЙФЭШРУП)

25. 90(О)+95(СДЧГ)=185(ОСДЧГ)

26. 106(ТН)+111(МЮЖБКЪ-ЬЩЦХ)=217(ТНМЮЖБКЪ-ЬЩЦХ)

27. 124(АИ)+139(Е-ЁЛЫЗ)=263(АИЕ-ЁЛЫЗ)

28. 161(ВЦЙФЭШРУП)+174(_)=335(ВЦЙФЭШРУП_)

29. 185(ОСДЧГ)+217(ТНМЮЖБКЪ-ЬЩЦХ)=402(ОСДЧГТНМЮЖБКЪ-ЬЩЦХ)

30. 263(АИЕ-ЁЛЫЗ)+335(ВЦЙФЭШРУП_)= 598(АИЕ-ЁЛЫЗВЦЙФЭШРУП_)

31. 402(ОСДЧГТНМЮЖБКЪ-ЬЩЦХ)+598(АИЕ-ЁЛЫЗВЦЙФЭШРУП_)=1000(ОСДЧГТНМЮЖБКЪ-ЬЩЦХАИЕ-ЁЛЫЗВЦЙФЭШРУП_)

В данном случае для некоторого отличия договоримся, что при определении значение кода мы будем использовать иную договоренность:

(!) При движении от корня к ветвям движение влево будет соответствовать 1, а движения вправо будет соответствовать 0.

Напомним, что при предыдущем построении дерева Хаффмана и определении значений кодовых слов латинского алфавита. мы применяли противоположную договорённость. А в данном договариваемся иначе.

Итак, мы рассмотрели статистику букв русского и латинского алфавитов. Однако если внимательно обратиться к этой теме, то станет понятно, что появление букв нельзя рассматривать как независимые события.

Зависимость букв русского алфавита в открытом тексте от предыдущих букв исследовалась выдающимся русским математиком Андреем Андреевичем Марковым. Он доказал, что появление букв в открытом тексте нельзя считать независимыми друг от друга, в частности им были подсчитаны частоты встречаемости биграмм - это пары букв вида гласных гласны – гласные, согласные – согласные, гласные и согласные, согласные и гласные. Просматривался текст длиной 10⁵ знаков, результаты подсчета отражены в таблице 12.

Таблица 12 – Частоты встречаемости биграмм

	Гласная	Согласная	Итого
Гласная	6 588	38 310	44 898
Согласная	38 296	16 806	55 102

Мы видим, что среди общего числа исследованных ситуаций, например, сочетание гласная- гласная встречалось 6588 раз. По этой таблице можно вычислить условные и безусловные вероятности, они могут служить некой оценкой соответствующих условных и безусловных вероятностей, вычисленных на текстах большего объёма. Из статистических исследований было получено, что вероятность биграммы гласная-согласная равна 0.663, согласная- гласная 0.872 и т.д. Можно сравнить эти результаты с теми, что приведены в таблице.

После зависимость появления букв в тексте исследовал методами теории информации Клод Шеннон. Им было показано, что эти зависимости носят весьма глубокий характер и ощущаются приблизительно в 30 знаков. Только потом статистическая зависимость практически исчезает. Были получены очень интересные результаты, показывающие насколько появления того или иного знака, под которым мы понимаем букву, зависит от предыдущих знаков. Из нашего опыта это понятно.

Если в предложении какое-то слово даже наполовину будет произнесено, мы всегда сможем достроить оставшуюся часть, исходя из понимания языка правил его формирования и того контекста, в котором оно употребляется. Говоря о статистике букв или слов, сочетаний букв, мы должны каждый раз ставить перед собой цель, которую мы хотим достичь в итоге. Понятно, что специализированные тексты, например,, в области физики, будут отличны от специальных текстов в области медицины или музыки. Поэтому если нас будет интересовать статистика на основе каких-то специализированных текстов, то необходимо провести соответствующие исследования. В среднем для того, чтобы познакомиться с результатами, почувствовать применимость методов в теории информации, нам вполне достаточно вероятности появления букв, о которых мы говорили.

На рисунке 32 изображён пример того, как используются знания о статистике встречаемости букв в латинском языке для построения клавиатуры, когда наиболее часто встречающиеся буквы - это на находятся в том месте, где это удобнее для оператора, работающего на этой клавиатуре.

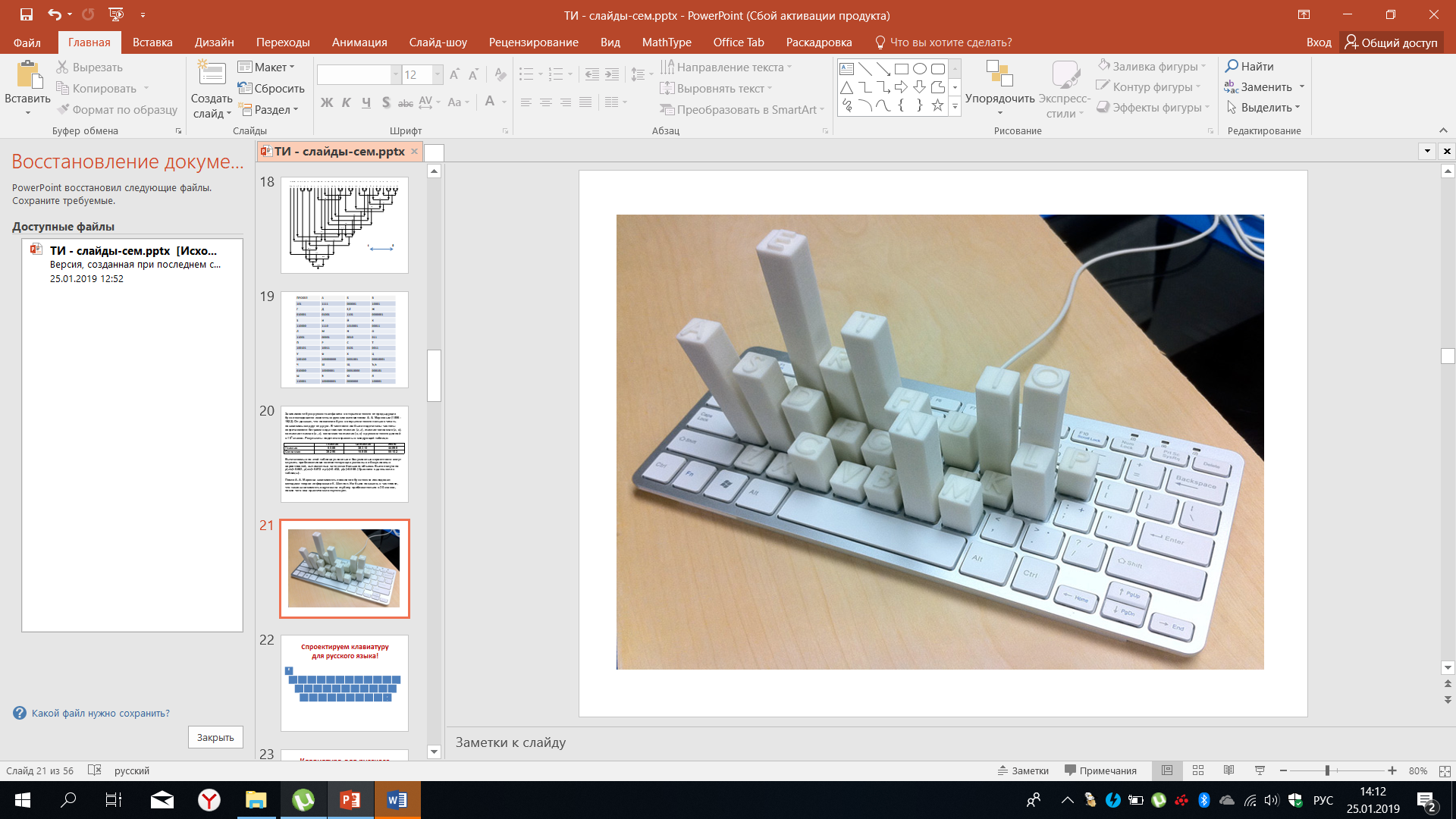
Рисунок 32 – Статистика встречаемости букв латинского языка на клавиатуре

Многие из нас работали на клавиатуре и понимают удобство расположения букв именно в таком порядке, а не по алфавиту. В порядке эксперимента попробуем определить, как расположены на клавиатуре буквы русского алфавита. Исходя из той статистики, которая нам известна, тот, кто хорошо владеет методом слепой печати, легко определиться с решением. Но для тех, кто не очень хорошо помнит, как расположены буквы на клавиатуре, это будет интересная задача. Итак, возьмём статистику частоты встречаемости букв русского алфавита и попробуем разместить их так, чтобы нам было удобнее печатать, используя как левую, так и правую руки.

После того, как вы попробовали решить задачу размещение букв на клавиатуре, с учётом частоты встречаемость этих букв и удобства печати, посмотрим на то решение, которое используется на практике в данном случае. Результат представлен на рисунке 33. Вы можете сравнить то, что было принято вами с тем, что принято в широко применяемых реальных клавиатурах. Надеемся, что совпадение было достаточно для того, чтобы дополнительно удостовериться в решение о размещении букв на клавиатуре.

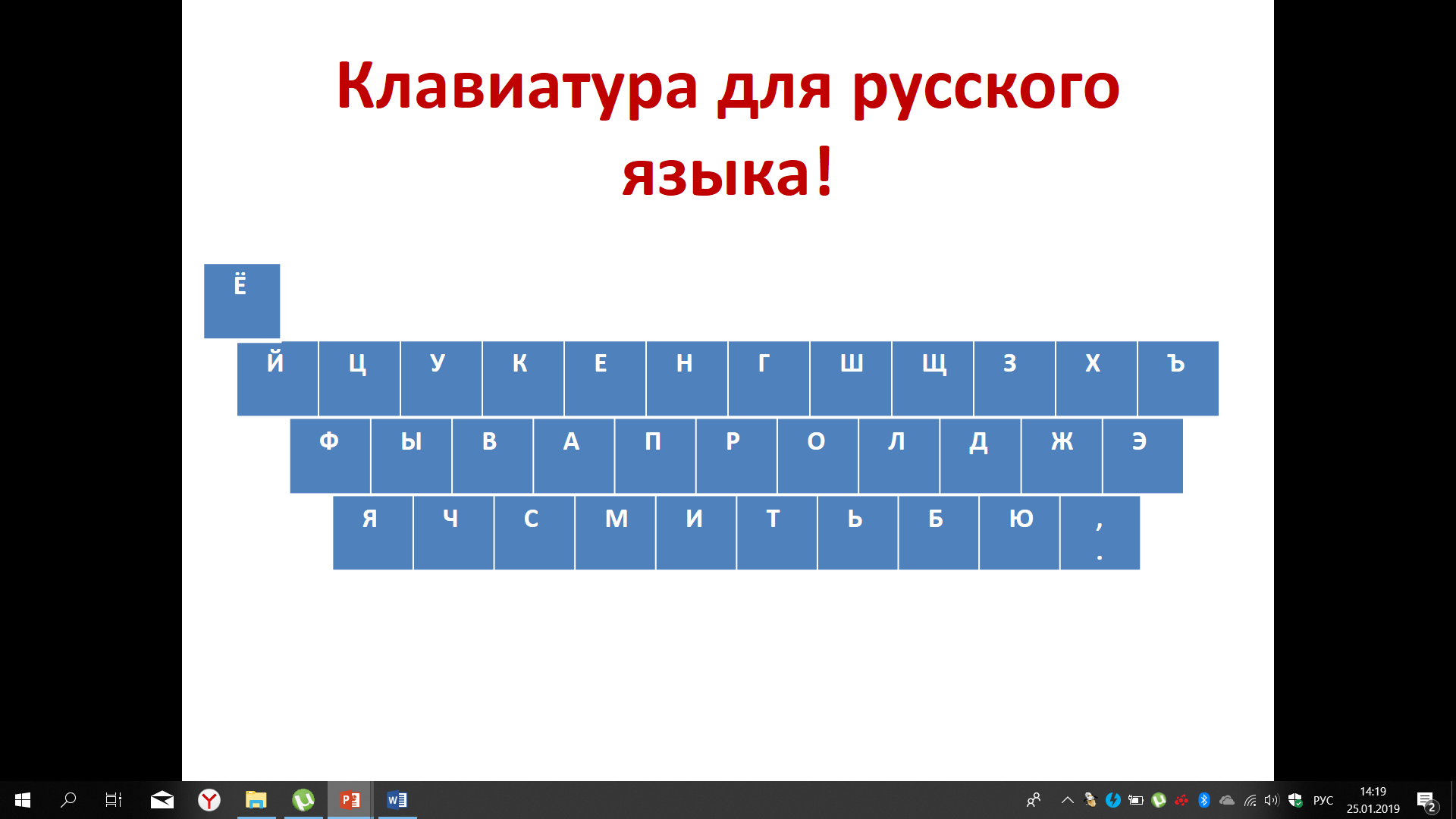
Рисунок 33 – Размещение русских букв на клавиатуре

Ещё раз посмотрим на реально существующие печатающие устройства и на реально существующие клавиатуры. Пример представлен на рисунке 34.

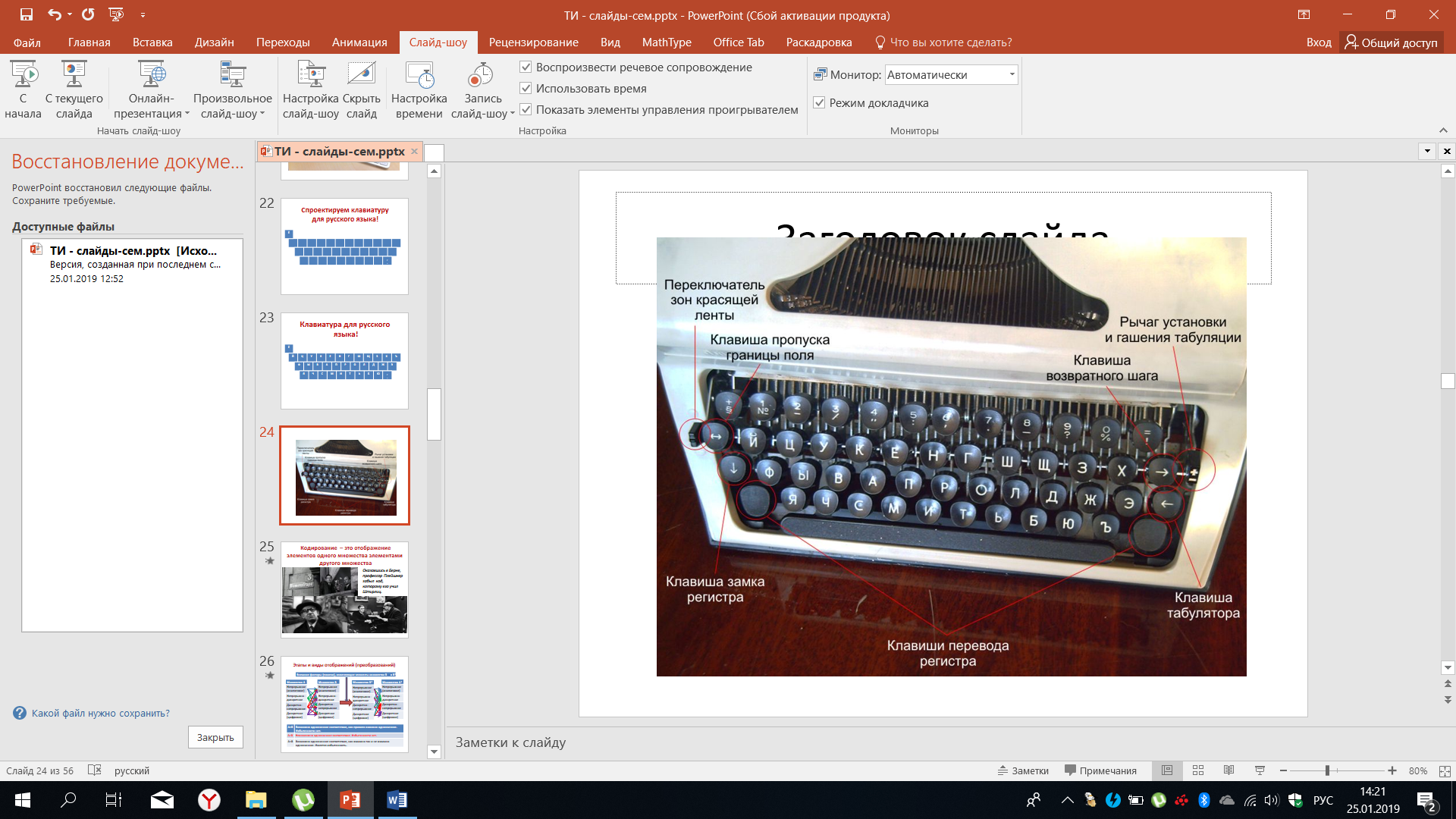
Рисунок 34 – Пример печатающего устройства

Мы рассмотрели случаи, когда те или иные сообщения, например, буквы русского или латинского алфавитов, отображаются с помощью кодовых комбинаций. Другими словами, с помощью чисел в различных системах счисления, чаще всего в двоичной системе счисления, если мы говорим о современных цифровых системах связи.

Кодирование - это отображение элементов одного множества элементами другого множества.

Отображение букв какого-либо алфавита в виде чисел - это кодирование. Вспомним, как в известном фильме профессор Плейшнер, оказавшись в Берне, забыл тот код, которому его учил Штирлиц. Он не заметил цветка в окне, забыл тот код, о котором они договаривались.

Попробуем подойти к этому с более общих позиций. Исходное множество А, которое сформирует исходное сообщение, может быть как непрерывным (аналоговым), непрерывно – дискретным, дискретно – непрерывным, так и дискретным (или цифровым). При преобразовании элементов этого множества в множество B (или другими словами, множество сигналов, которые передаются по линии связи), оно также может быть как непрерывным, так и непрерывно-дискретным, дискретно - непрерывным и дискретным. Ровно так же множество B*, соответствующее сигналу, принятому из канала связи, может быть в одном из четырёх указанных видов. Восстанавливаемые множество А* также может быть как аналоговым, так и цифровым, также непрерывно - дискретным или дискретно – непрерывным.

В современных системах связи все виды сообщений мы стараемся преобразовать к цифровому виду для того, чтобы была возможность использовать вычислительную технику, обрабатывающую эти цифровые сигналы. Далее цифровой сигнал преобразуется к тому виду, который максимально удобен для передачи по тому или иному каналу связи.

Вид сигнала выбирается таким, чтобы были согласованы его характеристики с характеристиками канала связи. Если мощности множеств совпадают, то возможно взаимно-однозначное соответствие. При этом избыточности нет, то есть каждой букве исходного сообщения ставится в соответствие определенная кодовая комбинация, их количество равно количеству различных кодовых комбинаций.

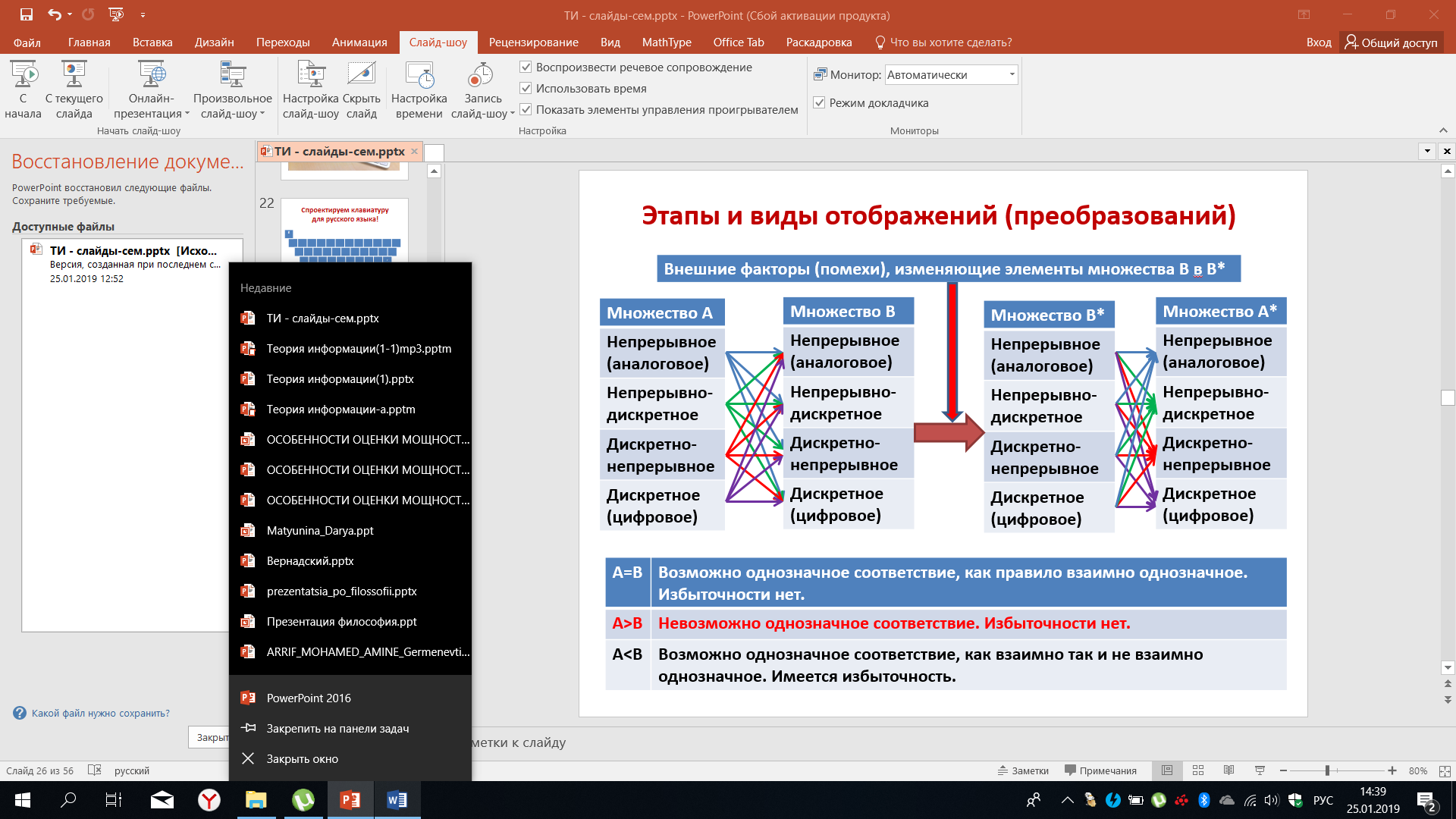
Рисунок 35 – Этапы и виды отображений

Если A > B, то невозможно однозначное соответствие. Избыточности нет на практике. Подобные ситуации, хотя и встречаются, но крайне. Если A > B, то это означает, что разные сообщения мы будем кодировать одной и той же кодовой комбинацией, что не позволит на приёме выявить различия. В случае, если A < B, то возможно взаимно-однозначное соответствие, возникает определённая избыточность, то есть часть кодовых комбинаций оказывается не задействованной для кодирования тех или иных сообщений.

Конечно, эту избыточность можно использовать для достижения дополнительных положительных результатов, что и делается для так называемых помехоустойчивых кодов, позволяющих обнаруживать и даже исправлять помехи в канале связи. Они строятся исходя из этой избыточности, то есть в этом случае принципиально выбирается такое соотношение, чтобы А было меньше B. Возникает избыточность, эту избыточность можно использовать для помехоустойчивого кодирования.

Если в целом попытаться охарактеризовать цели кодирования, то можно представить себе следующие:

1. первичное кодирование с целью достижения скорости кодирования, равной энтропии источника. В этом случае избыточность стремится к нулю. Это задача сводится к тому, чтобы минимизировать количество символов в кодовых комбинациях, приходящихся на одно сообщение.

Например, если у нас 8 сообщений и мы хотим закодировать каждое сообщение двоичным кодом, то мы должны потратить на одно сообщение 3 символа в кодовой комбинации. Но если сообщение появляется с неравный вероятностью, то, используя неравномерное кодирование, можно снизить количество символов, затрачиваемых на кодирование одного сообщения.

2. Выбор первичного кодирования с целью минимизации искажений элементов. Дело в том, что если множество А определено одной метрикой, а множество B и элементы множество B определены другой метрикой, то в конечном итоге нас будет интересовать минимизация искажений в множестве A.

Это довольно непростая задача, поскольку можно постараться минимизировать количество ошибок или искажения в множестве B, но это не означает, что будет достигнута минимизация в множестве A. Для каждого конкретного случая нужно искать решение. К сожалению, общего решения на сегодняшний день не существует.

3. Не взаимно - однозначное кодирование для достижения специальных целей. В данном случае этот пункт сформулированный несколько обще, означает, что, выбирая тот или иной способ кодирования, мы каждый раз должны хорошо себе представлять те цели, которые должны быть нами достигнуты при выборе способов кодирования.

Например, когда при плохой радиосвязи между собой люди ведут переговоры, они очень часто одно и то же важное слово повторяют несколько раз. Это и есть пример неоднозначного, не взаимно - однозначного кодирования. Если слово повторяется несколько раз, мы прекрасно понимаем, для чего это делается в условиях плохого приема. Нужно постараться обойти помехи, это достигается путем многократных повторов наиболее важных слов. В данном случае мы достигаем вот эту цель и это выделяется как отдельная цель кодирования.

4. Шифрование - это фактические изменения, связанные с изменением либо алфавита, либо последовательности (использование традиционного алфавита или дополнительные изменения, меняющие исходный закодированный сигнал в другой сигнал, в другое сообщение, по заранее оговоренному правилу).

Например, если мы договоримся, что традиционный белый цвет мы будем называть чёрным, тем самым мы внесем шифрование в передачу сообщения о цвете. Однако и на передаче и на приёме мы должны знать об этих изменениях для того, чтобы можно было восстановить исходное сообщение.

5. Согласование с характеристиками среды передачи, то, что относится к выбору того или иного вида сигналов, которые передаются по каналам связи.

Чаще всего здесь применяются методы, которые называют методами модуляции. В общем случае методы модуляции можно также классифицировать, как определенный методы кодирования.

6. Помехоустойчивое кодирование, которое можно реализовать при внесении дополнительной избыточности в сообщение или сигнал, отображающий исходный.

Если есть избыточность, ее можно конструктивно использовать для выявления возможных ошибок и даже их исправления.

Каждая из этих целей заслуживает отдельного рассмотрения, здесь не существует абсолютно исчерпывающих общих решений.

Поговорим немного о защите информации. Защита информации базируется на криптографии и криптоанализе.

Криптография - это раздел прикладной математики, изучающий модели, алгоритмы, программные и аппаратные средства, преобразования информации для шифрования в целях сокрытия содержания, предотвращения видоизменений несанкционированного использования.

Криптография даёт возможность преобразовывать сообщение таким образом, что прочтение, восстановление содержащиеся в нём информации, возможно только при знании ключа. Например, во времена, когда складывалась письменность. История доносит до нас что те, кто владеет этой письменностью, специально вносили определённые сложности в прочтении письменной речи по сравнению с тем, как в отдельности произносится те или иные звуки. Это характерно для известных французского и английского языков. Это своеобразная шифрование, защита от тех, кто не был посвящен в секреты прочтения письменных текстов.

Криптоанализ - это раздел прикладной математики, изучающий модели, методы, алгоритмы программные и аппаратные анализы, криптосистемы или её входные и выходные сигналы, это дешифрование с целью извлечения конфиденциальных параметров, включая открытый текст.

Совокупность криптография и криптоанализа составляет основу криптологии. В криптологии широко используются методы теории вероятности. Криптология будет больше всего интересоваться применимостью теории информации в качестве сообщений, подлежащих шифрованию и расшифровыванию. Рассматриваются тексты, построенные на некотором алфавите.

Алфавит - это конечное множество, используемое при кодировании информационных знаков.

Текст - это упорядоченный набор из элементов алфавита.

Самое простое - это алфавит, состоящий из букв русского алфавита, а текст - это то, что мы с вами привыкли читать. Однако в общем случае, и в особенности в плане применимости для искусственных информационных систем, компьютеров, примером алфавита чаще является алфавит, состоящий из двух знаков, из двух элементов.

Обозначим:

Z₂ - двоичный алфавит {0,1};

Z₈ и Z₁₆ - восьмеричный и шестнадцатеричный алфавиты;

Z₂₅₆ – символы, входящие в стандартные коды ASCII и КОИ-8;

Z₃₃ – 32 буквы русского алфавита (исключая Ё) + 1 пробел.

Можно предложить множество других алфавитов, мы знаем примеры этому. Например, телеграфный аппарат, построенный на азбуке Морзе. В этом случае алфавит включает в себя точку, тире и паузу. Говоря о представление в виде электрических сигналов: короткий сигнал, тире (длинный сигнал), пауза в передаче сигналов. Наверное, есть свой алфавит и у пчёл, и у других живых существ, которые умеют передавать и принимать информацию. Обычно простейшие система шифрования изображается так, как представлено на рисунке 36.

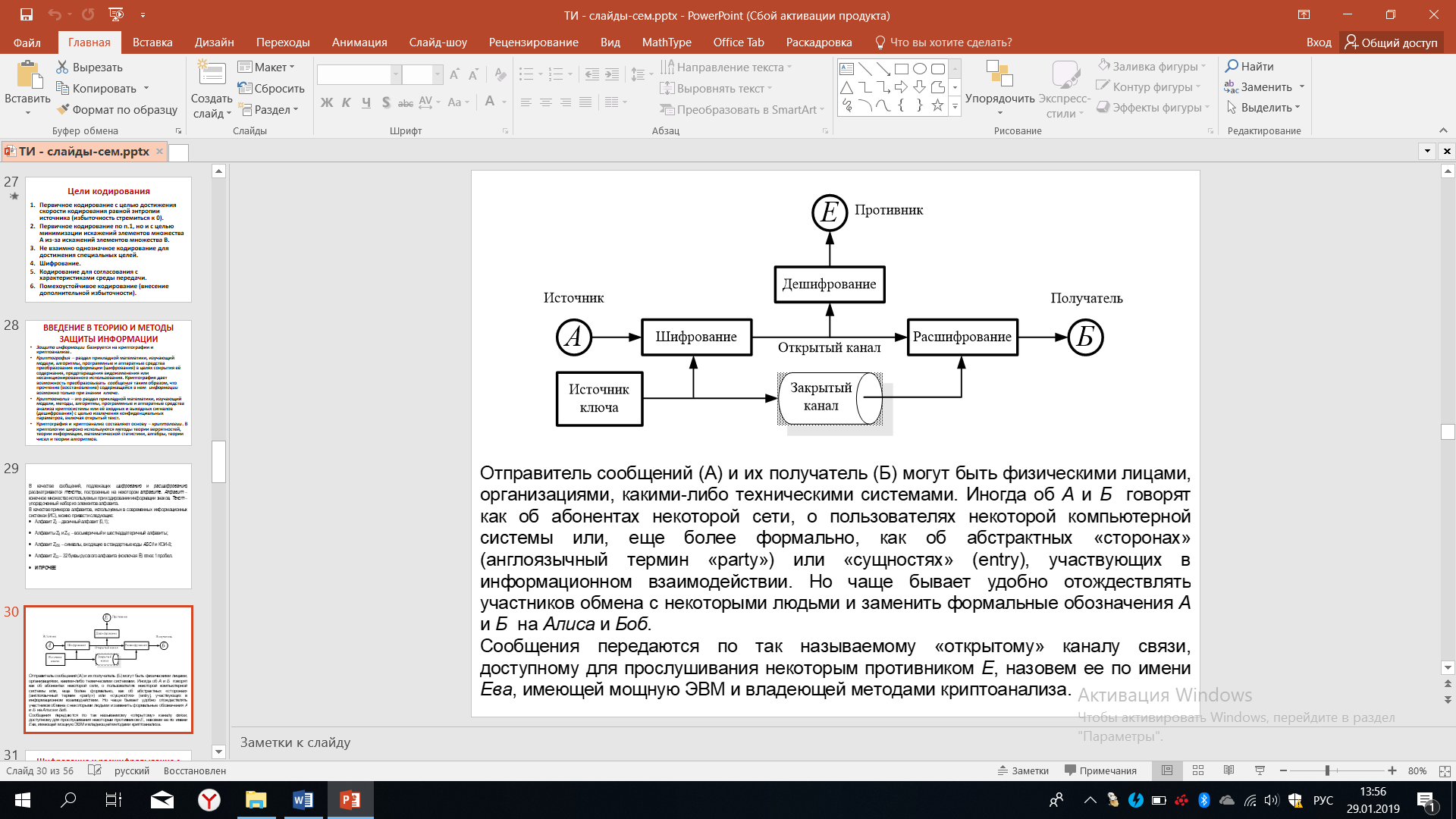
Рисунок 36 – Система шифрования

Отправитель сообщения A (или источник) и получатель сообщений Б, которые могут быть физическими лицами, организациями или компьютерами, техническими системами. Зачастую они рассматриваются как абоненты некоторые сети, как определенные стороны или сущности, участвующие в информационном взаимодействии.

Повелось так, что этих двух участников (A и Б) отождествляют с некими личностями, которых зовут Алиса и Боб. Сообщение передается по так называемому открытому каналу связи, для открытой линии связи и в силу своей открытости этот канал доступен для прослушивания некоторым противником Е. Продолжая уже имеющуюся договоренность об Алисе и Бобе, назовем этого противника по имени - Ева и будем полагать, что Ева имеет достаточно мощную вычислительную технику, владеет методами криптоанализа и может несанкционированно дешифрировать ту информацию, которая передается от источника.

Мы видим, что информация шифруется, передается через открытый канал, расшифровывается на приёме и выдается получателю. Противник его подслушивает и может дешифрировать то, что передается по открытому каналу. Для того, чтобы на приёме можно было расшифровать поступающие сообщение, надо знать ключ. Можно заранее об этом договориться, а можно передавать этот ключ, изменяя его время от времени для того, чтобы усложнить Еве дешифрирование сообщения. Тогда информация о ключе должна передаваться по закрытому каналу. Под понятием закрытого канала подразумевается тот канал, к которому противник не сможет получить доступ, а если сможет, то вероятность такого события должна быть крайне мала.

Разберем один из наиболее простых и понятных способов шифрования и расшифровывания, которое называют кодом Цезаря. Известно, что император Цезарь использовал этот метод для шифрования своих сообщений.

Суть этого метода в следующем:

Если n {\displaystyle n} - количество букв в алфавите,

m j {\displaystyle m_{j}} - номер буквы из открытого текста,

k j {\displaystyle k_{j}} - ключ (целое число),

то зашифрованная буква по коду Цезаря имеет номер:

c j = m j + k j ( mod n ) {\displaystyle c_{j}=m_{j}+k_{j}{\pmod {n}}} ,

при расшифровывании:

Например, при буква «А» станет «Г», а буква «Ю» - «Б».

Например, если взять буквы русского алфавита и выбрать первую букву А, букву имеющую номер 1 и прибавить к ней число 3, а число 3 - это выбранный ключ, то мы получим число 4, что будет соответствовать букве Г.

Способ кодирования по коду Цезаря достаточно прост и при определённом старании можно добиться вскрытия этого кода, даже не зная ключа. То есть можно очень быстро узнать то, о чём между собой разговаривают Боб и Алиса. Попробуем и мы сделать это. Предположим, что было передано слова МЕЬКЧ. На рисунке 37 мы видим это слово, заключенная в кавычки. Конечно, не просто догадаться, что это за слово. Однако составим таблицу, где укажем все возможные ключи.

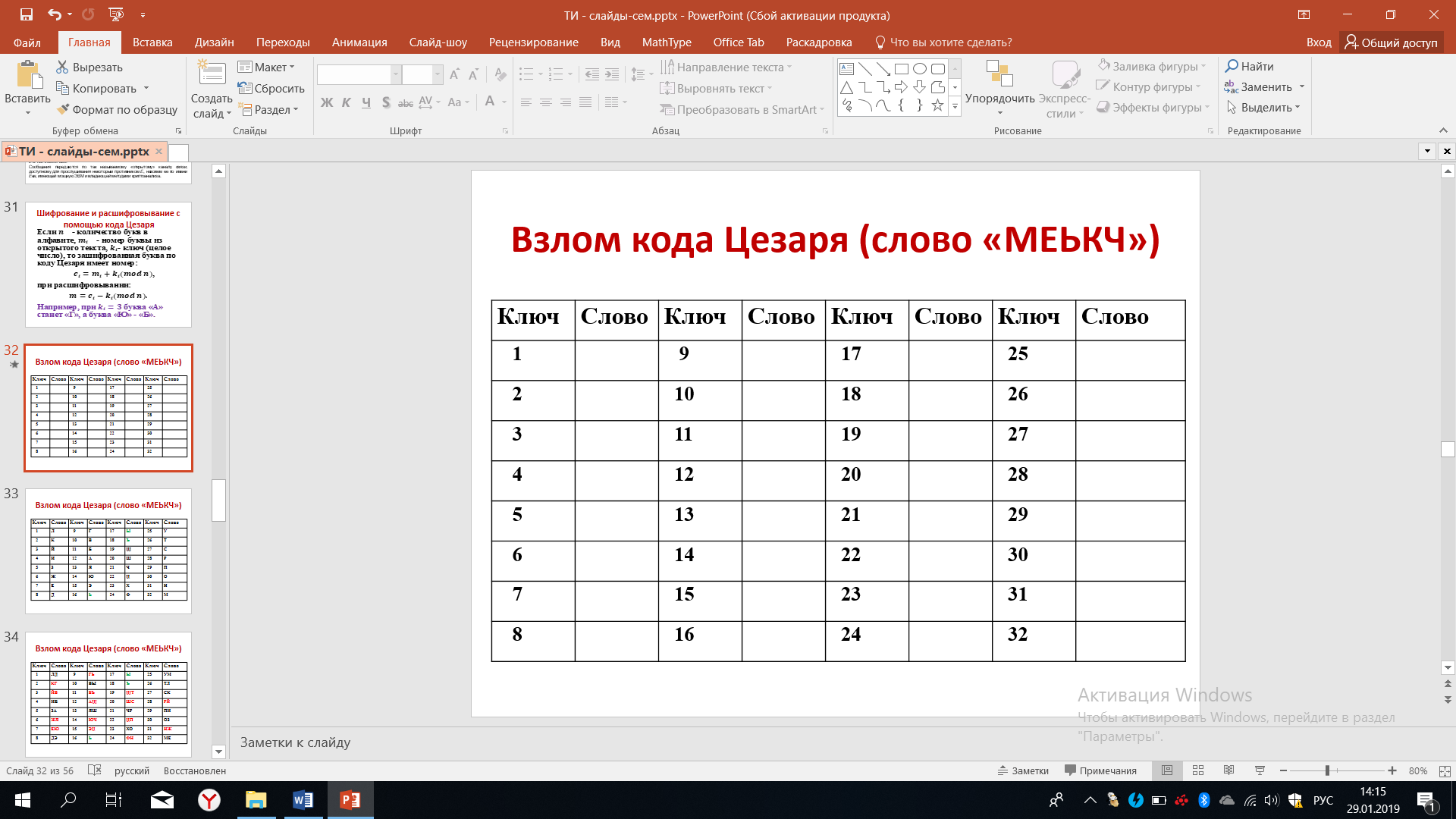
Рисунок 37 – Таблица ключей кода Цезаря

Поскольку используется алфавит из 32 букв, то понятно, что ключ может принимать одно из 32 значений. Итак, расшифруем первую букву М. Если ключ был равен единице, если ключ был равен двум, если ключ был равен трём и так далее.

Если ключ был равен единице, то это означает что буква М в исходном случае было буквой Л, если ключ был равен двум, то буква М была буквой К и т.д. Однако уже после первого опыта мы можем исключить из рассмотрения включи равные 16-17-18, потому что мы знаем, что в русском языке не существует слов, начинающихся на ь, на букву ы или на ъ.

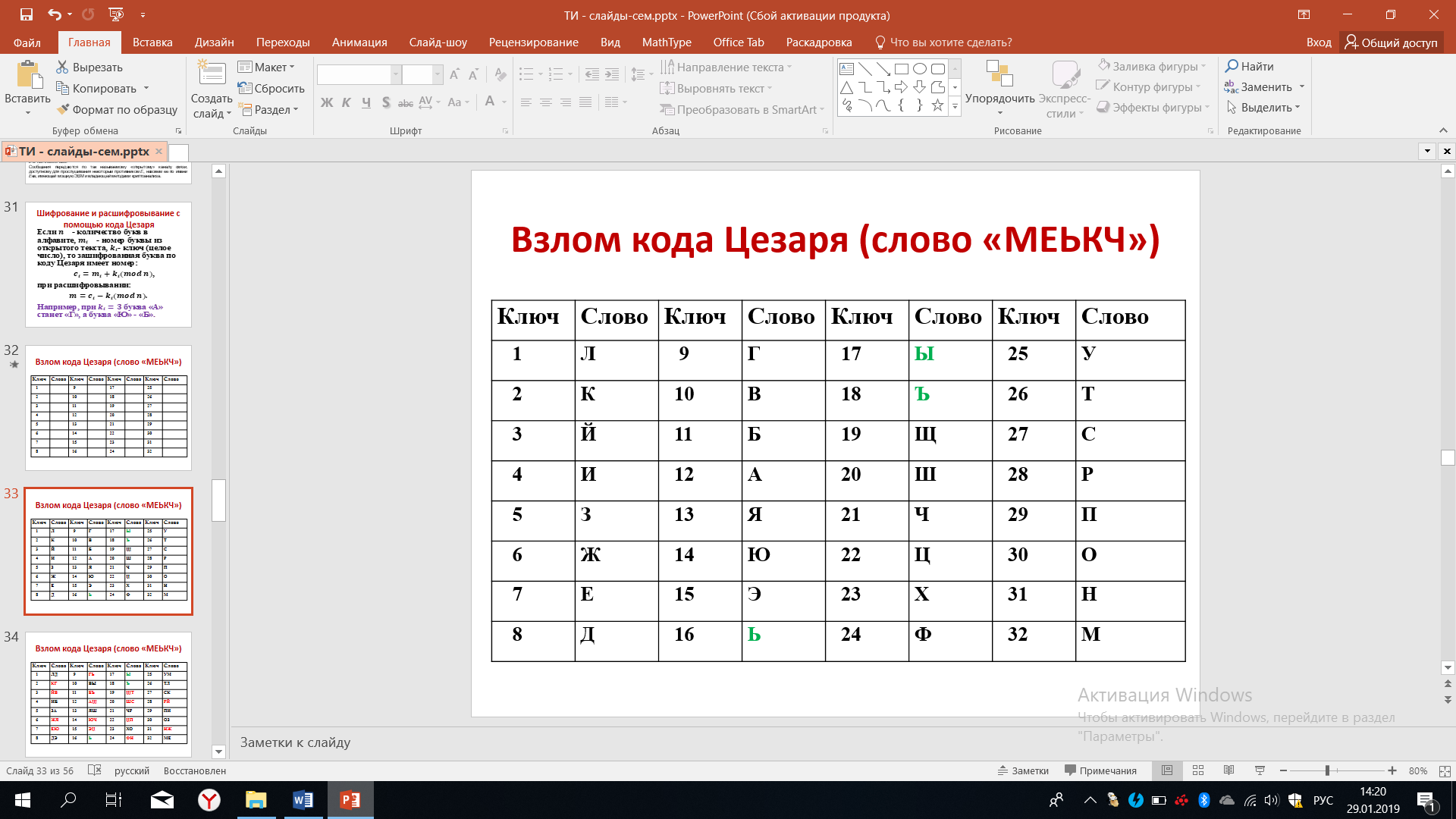
Рисунок 38 – Расшифровка буквы М

Теперь расшифруем букву Е, вторую букву слова для всех оставшихся ключей, если ключ равнялся единице, буква Е будет расшифрована как Д и т.д. При этом шаге мы можем отбросить ещё целый ряд расшифрованных пар.

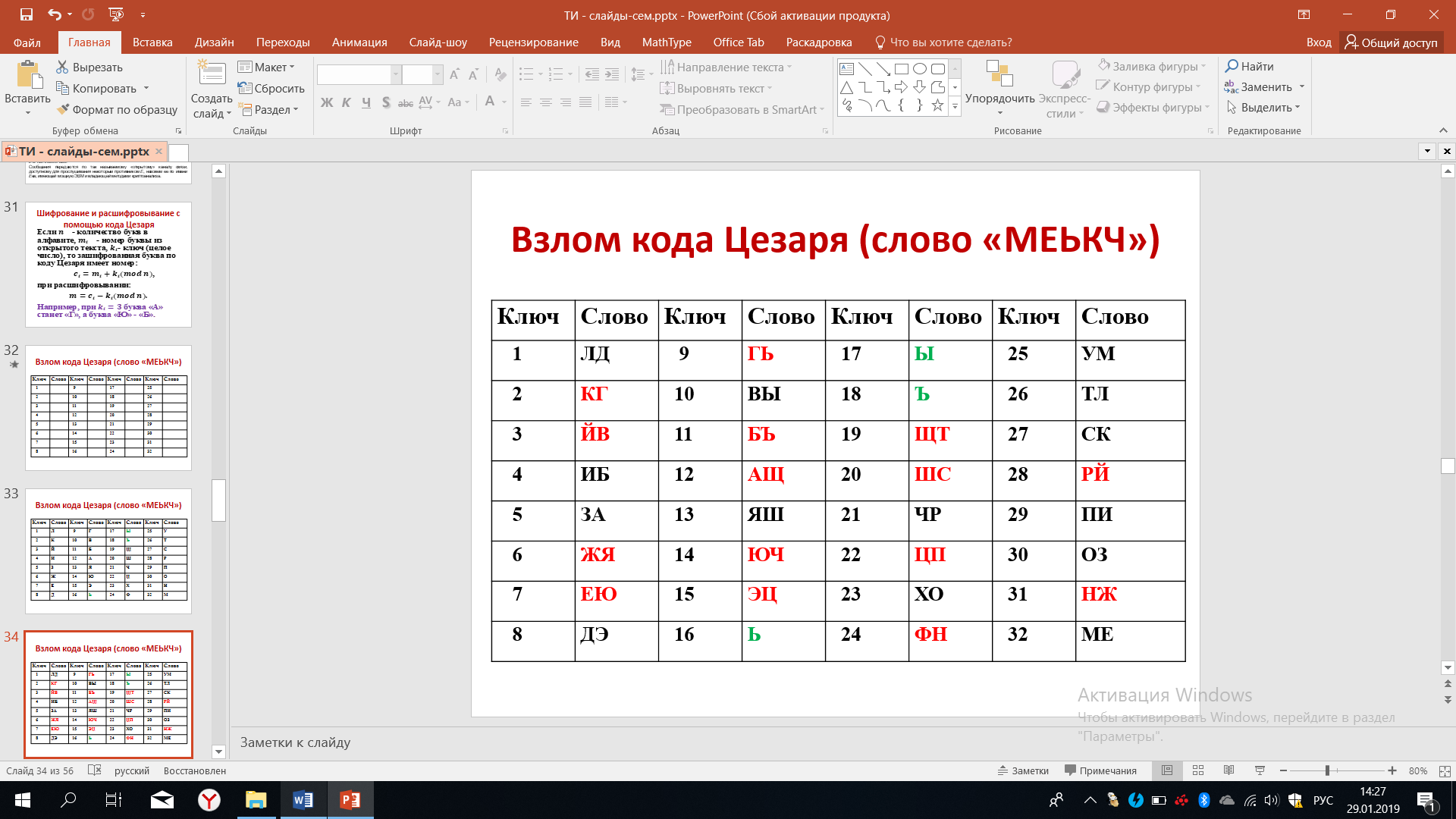
Рисунок 39 – Расшифровка буквы Е

Продолжим расшифровывать третью букву. В этом случае количество возможных вариантов ключей ещё больше уменьшится, останется всего 3 варианта, что представлено на рисунке 40. Во всех других случаях складываются слова, которых нет в русском языке.

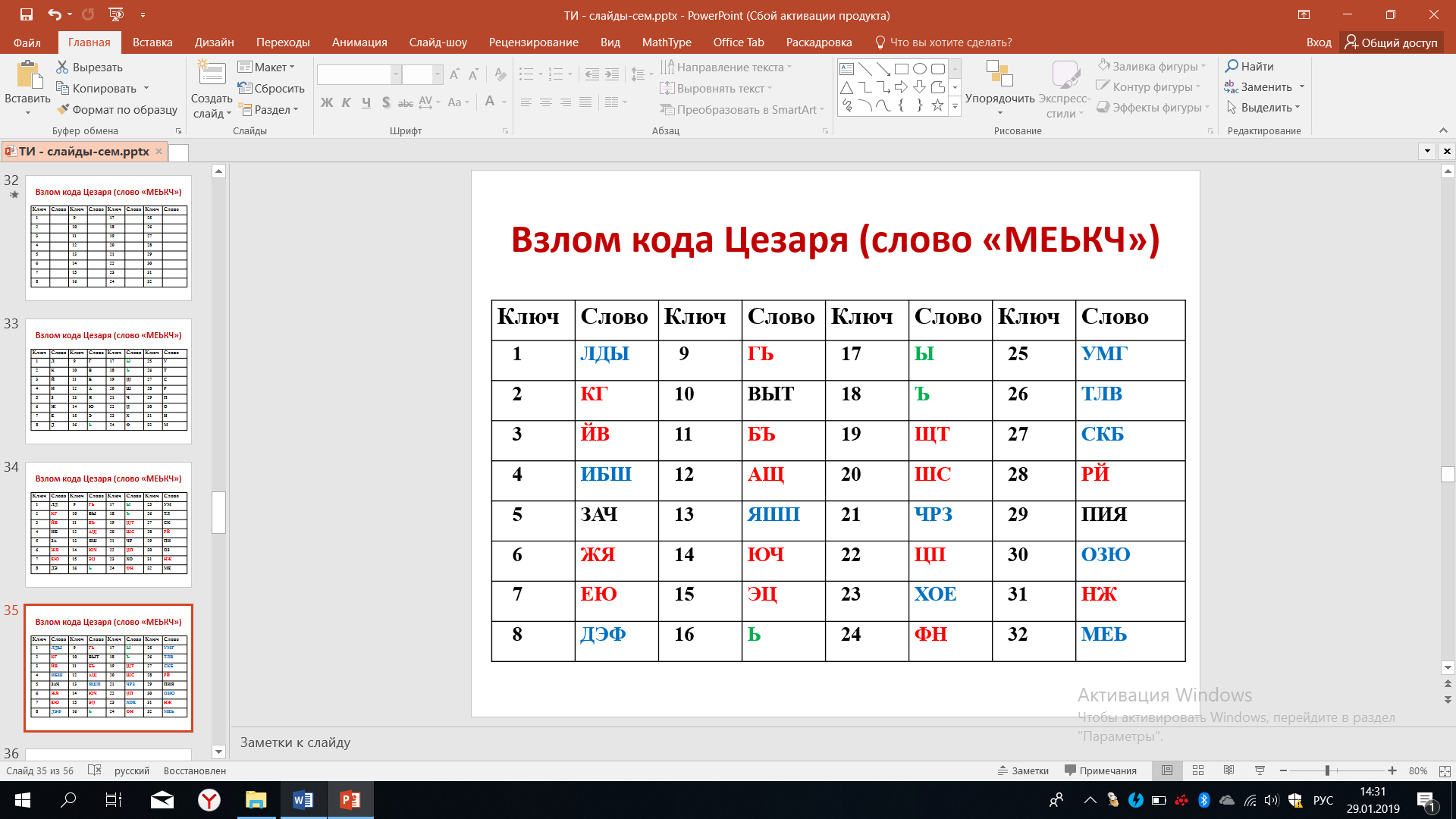
Рисунок 40 – Расшифровка буквы Ь

После расшифровывания 4-й буквы останется два слова – ЗАЧЕ и ПИЯН.

Рисунок 41 – Расшифровка буквы К

Наконец, расшифровывание 5-й буквы приводит к тому, что мы получаем единственно верное слово ЗАЧЕТ при ключе равном 5. Не так много времени нам потребовалось для того, чтобы осуществить расшифровку, а компьютер это сделает намного быстрее.

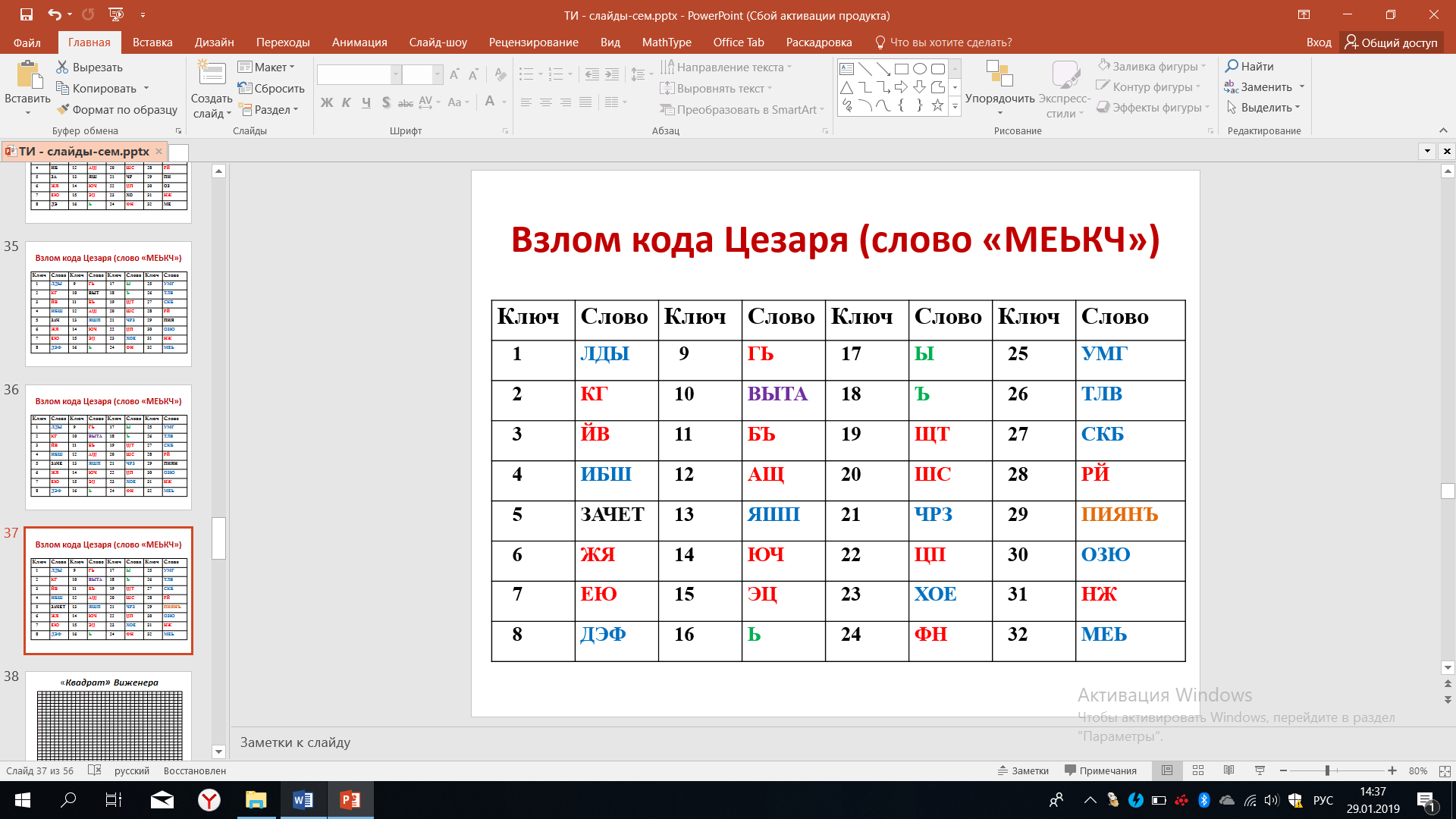
Рисунок 42 – Расшифровка буквы Ч

Рассмотрим еще один способ шифрования, с помощью так называемого квадрата Виженера, названного по имени того, кто первым предложил подобный способ и то, как строится этот квадрат, который на первый взгляд кажется очень сложным, но на самом деле он поддается определённому правилу.

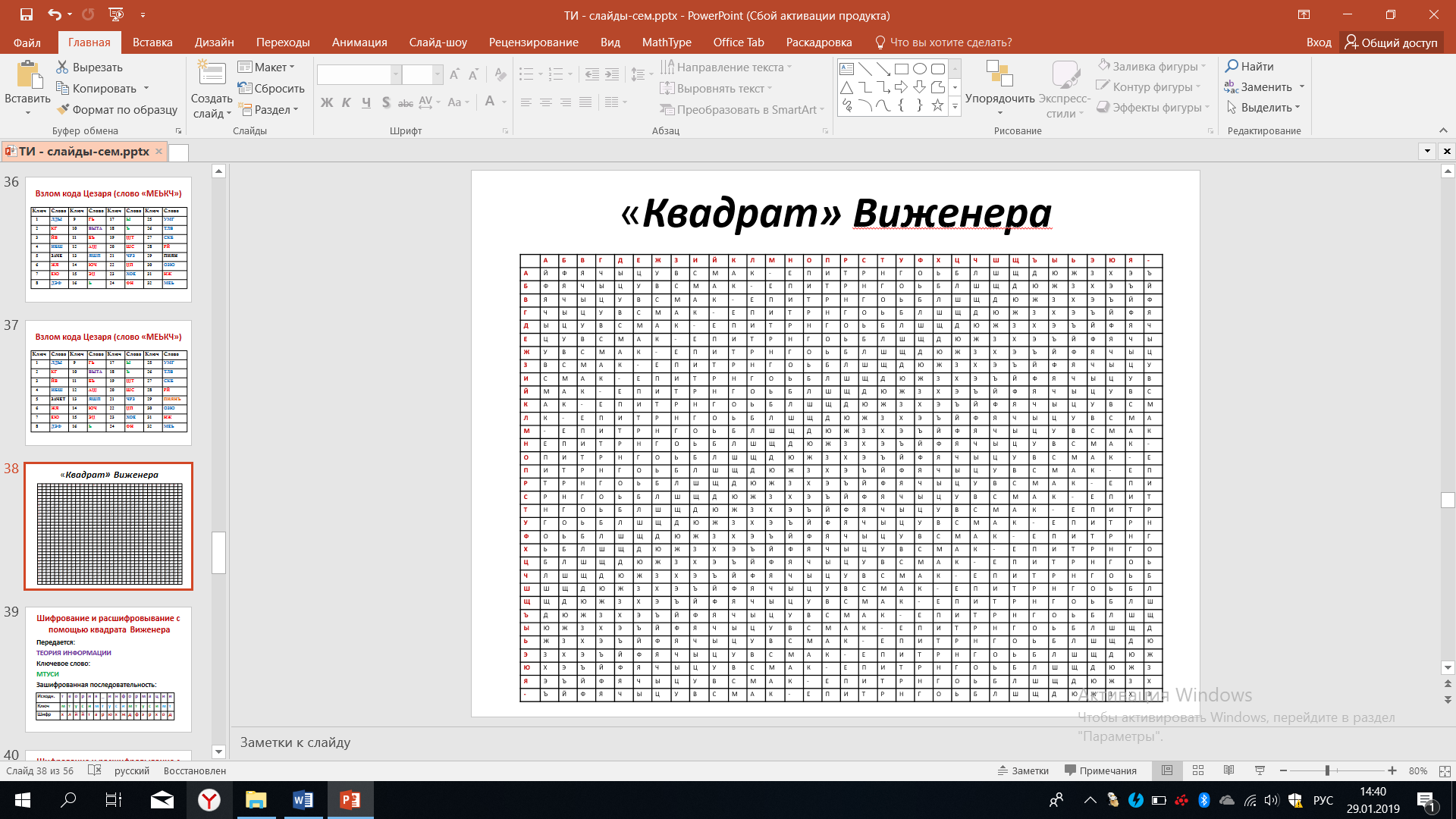
Рисунок 43 – Квадрат Виженера

Верхняя строчка - это алфавит в принятом порядке. Первый слева столбец - это тот же алфавит, в принятом порядке. Таким образом квадрат Виженера - это матрица, соответствующей размерности. Первая строчка квадрата, которая в нашем примере начинается с буквы Й, вторая буква Ф, третья буква Я, четвертая буквы Ч и т.д., соответствует совершенно произвольному выбору последовательности букв русского алфавита. Другими словами, тот алфавит, который был изображён красным цветом в верхней строчке, произвольным образом перепутан во второй строке.

Нам необходимо вписать все буквы алфавита в произвольном порядке. Нами был выбран тот порядок, который предложен в данном примере. Вторая строчка квадрата, изображённая чёрным цветом, соответствует первой строчке, смещенной на один разряд влево.

Посмотрите, из первой строчки чёрного цвета буква Ф сместилась влево на один разряд. Третья строчка - это первая строчка, смещенная на два разряда или вторая строчка, смещенная влево на один разряд. В дальнейшем, повторяя все эти процедуры, мы заполняем все оставшиеся строчки квадрата Виженера. По договоренности можно смещать буквы не влево, а вправо, это не внесет каких-либо существенных изменений, но об этом надо договориться сразу.

Разберем пример шифрования с помощью квадрата Виженера. Предположим, мы хотим передать два слова - теория информации. В качестве ключевого слова или ключа выберем название нашего университета – МТУСИ.

А теперь составим таблицу, в первой строчка которой записывается передаваемая информация – «теория информации», во второй строчке записываются ключи, следующие друг за другом: МТУСИ, МТУСИ, МТУСИ, как на рисунке 44.

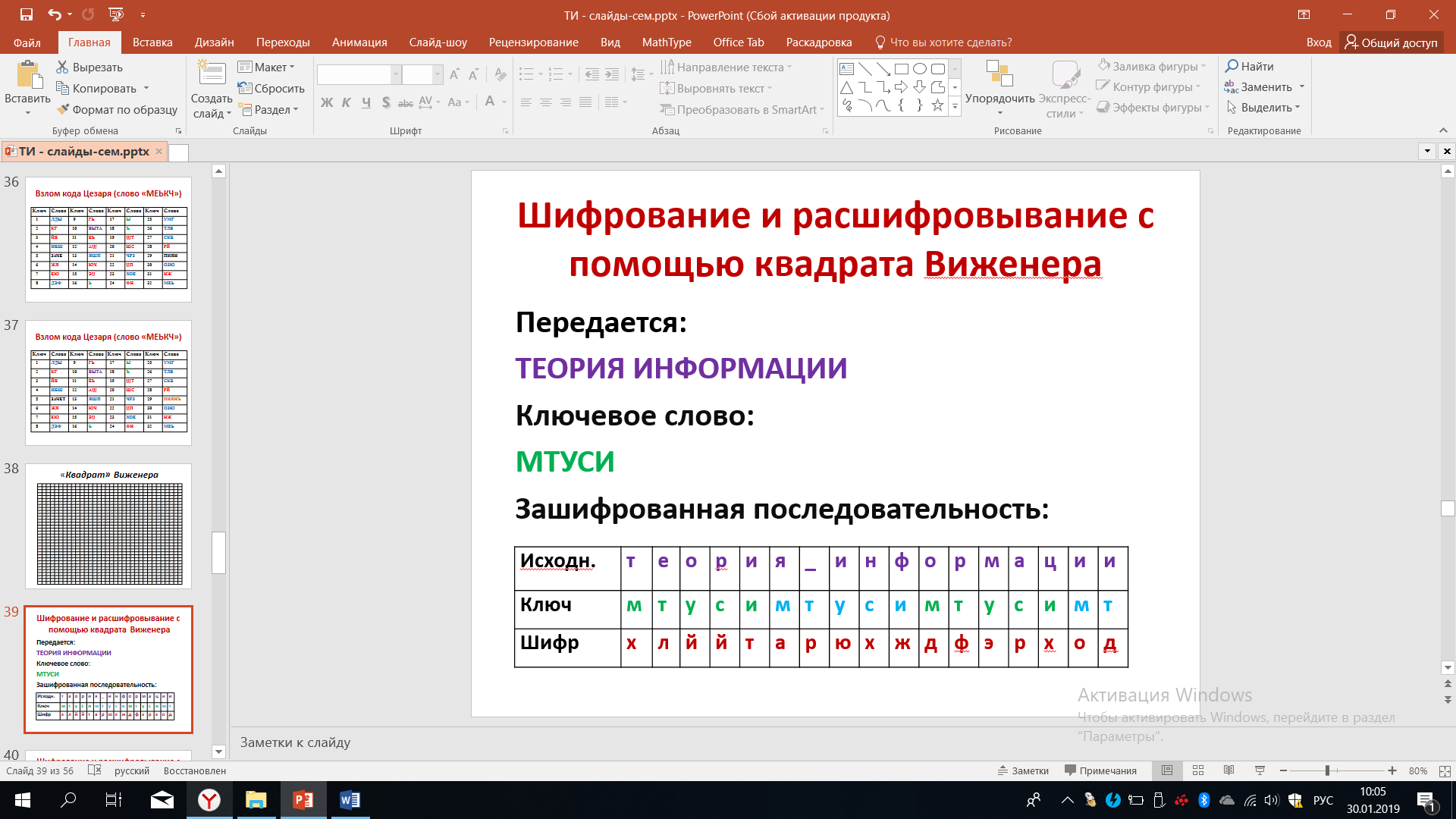
Рисунок 44 – Шифрование по квадрату Виженера

Первая буква исходного сообщения - буква Т. Находим эту букву в крайне левой части матрицы Виженера, в самом первым столбце. Итак, мы нашли букву Т, теперь выбираем строчку, которая начинается с найденной буквы. Далее в первой строке квадрата Вижинера ищем первую букву ключа - М (ту, которая записана под нашей буквой Т) и выбираем столбец, который будет опускаться вниз от буквы М. На пересечении выбранного столбца и строки мы находим букву Х.

Продолжаем дальше: в левом столбики находим букву Е, фиксируем эту строчку. В верхней строке находим букву Т, фиксируем соответствующий столбик. На пересечении строчки, начинающейся с буквы Е со столбиком, начинающимся с буквы Т, мы находим букву Л. Продолжая дальше, мы находим все остальные буквы зашифрованного текста, он в таблице представлен в последней строчке. Пытаться, прочитав его, понять, что зашифровано - крайне сложно.

Расшифровывание последовательности букв с помощью квадрата Виженера происходит в обратном порядке. На приеме мы знаем ключ - МТУСИМТУСИМТУСИМТ, поэтому в крайнем левом столбике квадрата Виженера находим букву М и, оттолкнувшись от этой буквы, в её строчке находим букву Х. Обнаружив букву Х, мы двигаемся наверх, где в первой строке квадрата по нашему столбцу обнаружим букву Т. Далее по крайнему левому столбику мы находим вторую букву ключа - букву Т и, оттолкнувшись от неё вправо, по данной строчки мы разыскиваем букву Л. Обнаружив букву Л, двигаемся по столбику вверх и обнаруживаем, что это соответствует букве Е в верхней строчке.

Далее, будучи достаточно внимательным, можно легко осуществить расшифровывание поступившей информации и восстановить исходное сообщение – «теория информации». Но уже при использовании такого квадрата Виженера мы начинаем испытывать определенные трудности. А в компьютерной реализации всё выглядит намного проще, главное, что при ней практически не будет ошибок при шифровании и расшифровывание, если кто-то, конечно, намеренно не стремится допустить ошибки.

Обратимся к рисунку 45, на котором показаны методы аналого-цифрового преобразования. Мы видим, что основным в решении этой задачи является квантование и дискретизация, которые позволяют непрерывный сигнал представить в виде последовательности отсчетов, а затем каждый отсчет в соответствии сего значением кодируется, исходя из той кодовой комбинации, которая соответствует определенному уровню.

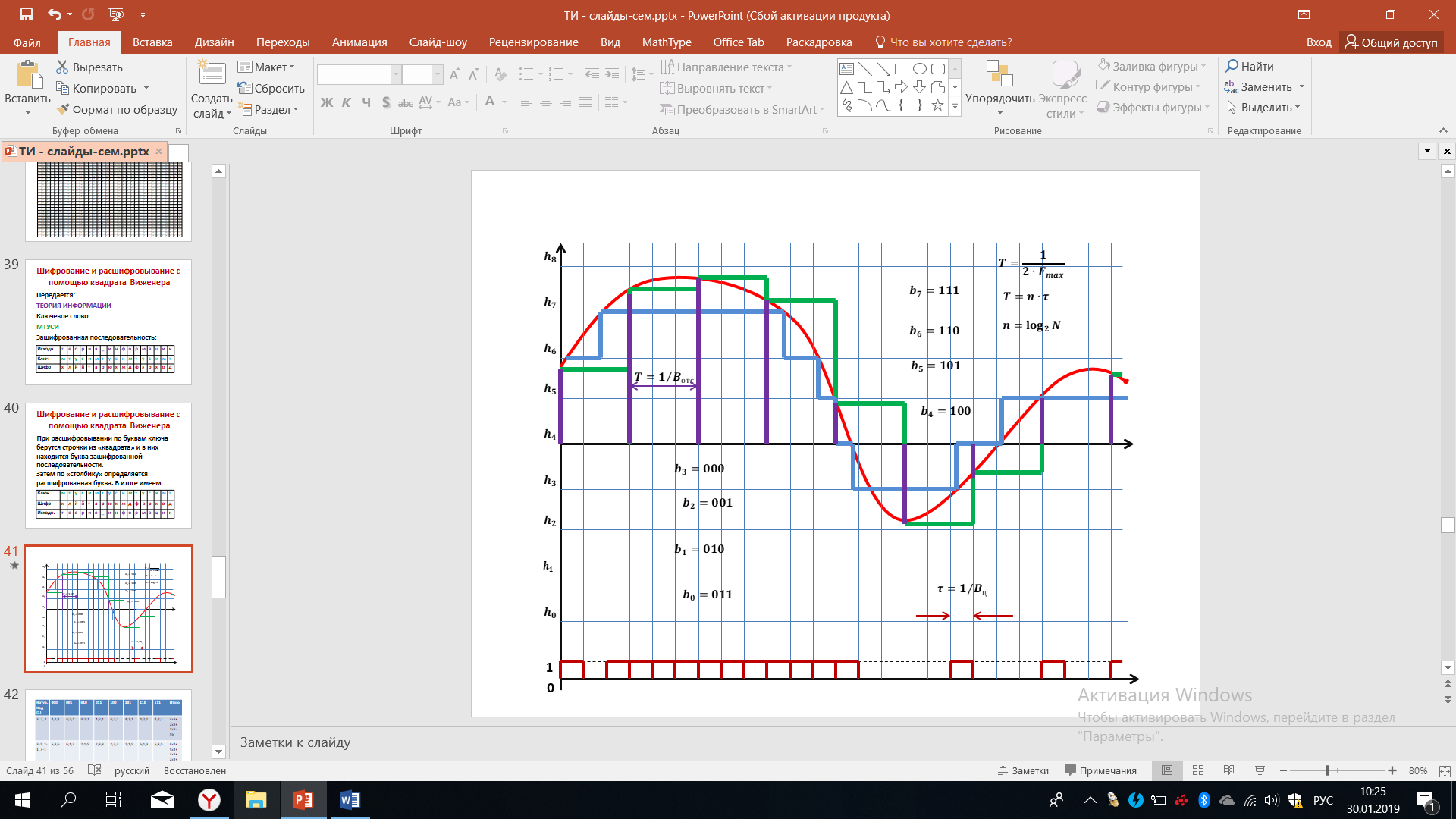
Рисунок 45 – Аналогово-цифровое преобразование

В данном примере выбрано 8 уровней, поэтому мы имеем 8 кодовых комбинаций: b₀,b₁,…,b₇, каждый из которых состоит из 3 символов и соответствует определенному уровню. Обратим внимание на то что, b₀ в данном примере соответствует кодовой комбинации 011, b₁ выбирается равный кодовой комбинации 010, b₂ выбирается равный кодовой комбинации 001 и т.д. На самом деле можно выбрать и другие способы кодирования, например, в виде двоичной кодовой комбинации отражать номер уровня: 4й уровень - 100, 5й – 101, 6й – 110, 7й – 111.

Мы видим, что в верхней части так и сделано: двоичные кодовая комбинация соответствует определенным десятичным цифрам, а в нижней части принят инверсный способ кодирование. Всего может быть много различных способов кодирования, а именно (2ⁿ)!, где n=log₂N - число символов в кодовой комбинации. Выражение под факториалом в нашем случае 2³=8, а общее число разных кодовых комбинаций - 8!.

Мы видим, что число различных вариантов кодирования нарастает очень и очень быстро. Оказывается, что в определённых случаях из-за влияния помех в канале связи, которые будут искажать цифровой сигнал, представленной кривой на рисунке. При последующем восстановление определённые методы кодирования уровней будут иметь преимущество. Исследуем этот вопрос.

Давайте вспомним формулы, показанные в верхней части рисунке 45, которые устанавливают соответствие между интервалом дискретизации Т и максимальной частотой спектра непрерывного сигнала, соответствие между интервалом дискретизации и длительностью элементов цифрового сигнала (показанного внизу), а также соответствие между числом символов в кодовой комбинации и значениями отчетов, общим количество отсчетов. Эти величины связаны через логарифм. Перейдем к изучению того, как способы кодирования отсчетов могут влиять на качество восстановления сигналов при действии помех и возникновения ошибок в цифровом дискретном сигнале.

Рассмотрим первый вариант кодирования уровней квантования так называемым натуральным кодом. В этом случае уровню h₀ соответствует кодовая комбинация – 000, уровню h₁ - 001 и т.д. В натуральном коде номеру уровня в десятичной системе счисления соответствует кодовая комбинация в двоичной системе счисления.

В верхней части таблицы 13 приведены восемь различных кодовых комбинаций, соответствующих слева-направо уровням h₀, h₁, h₂,…, h₇.

Таблица 13 – Натуральный код

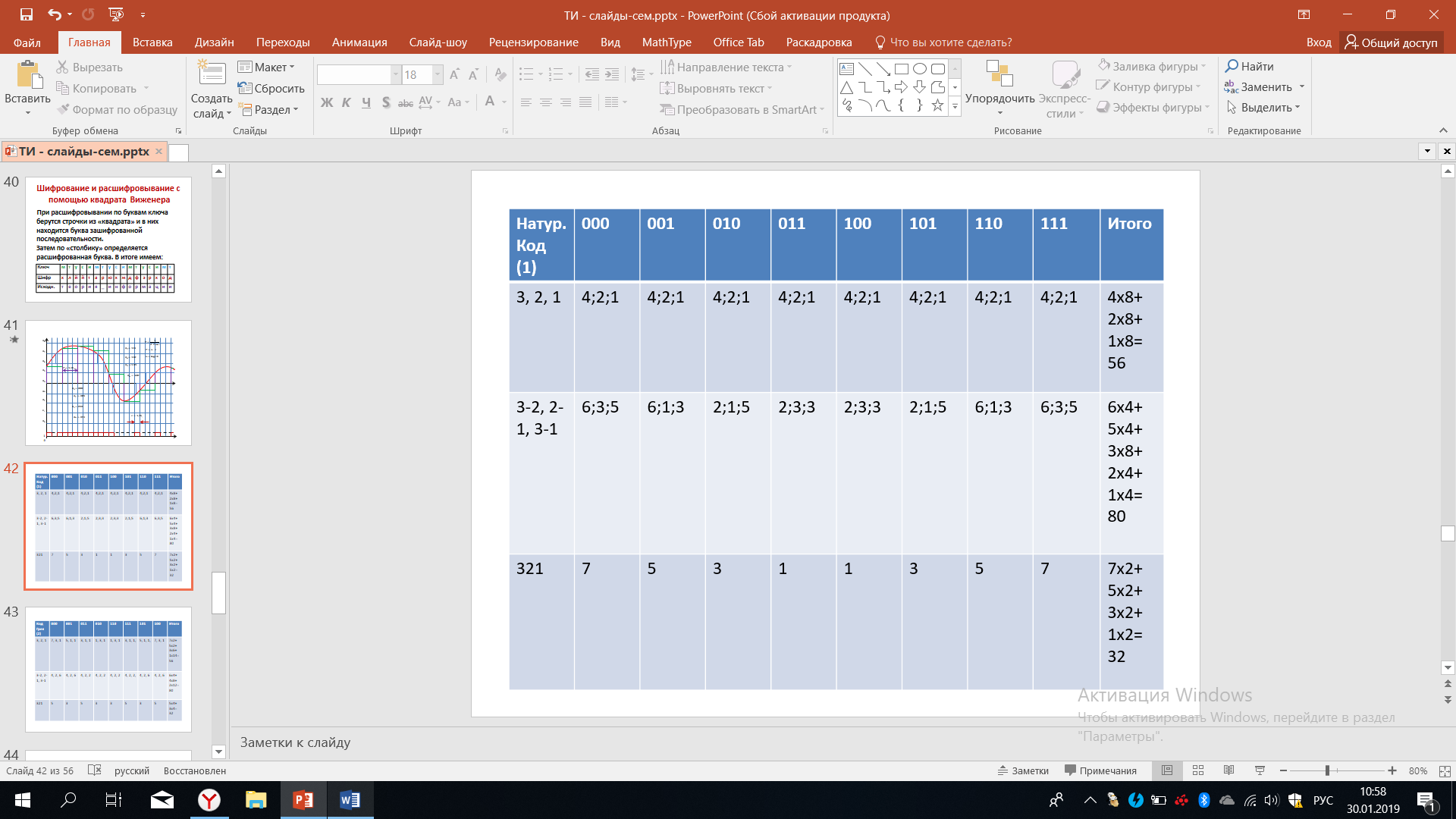
Из-за действия помех могут возникать ошибки в кодовых комбинациях, при этом может быть искажен только один символ или два, или даже 3. Давайте последовательно рассмотрим все возможные варианты. Условимся кодовые комбинации, которые показаны в верхней строке, нумеровать справа-налево, например, для кодовой комбинации соответствующие уровню h₁, a именно кодовой комбинации 001, первым символом будем называть правую единичку, центральный символ будет вторым (это символ 0) и, наконец, третий символ (самый левый) это тоже 0.

В левом столбике этой таблицы, во второй строке указаны цифры 3, 2, 1 - это в наших условных обозначениях будет соответствовать тому, что искажен соответствующий (ошибочно принят соответствующий) символ кодовой комбинации. Итак, начнем рассмотрим цифру 3 - это означает, что третий символ в кодовой комбинации меняет свое значение.

Первая кодовая комбинация – 000. Что произойдет, если третий символ в этой кодовой комбинации будет искажен? Если этот символ будет искажен, то кодовая комбинация превратится в комбинацию 100. Давайте найдём такую кодовую комбинацию в верхней строчке. Мы видим, что комбинация 100 стоит от кодовой комбинации 000 на 4 уровне (шага по строке) правее, что мы и отметим во второй строчке - ставим цифру четыре, после которой точку с запятой.

Следующую ситуацию мы будем рассматривать при сбое или при искажении при ошибочном приеме второго символа. Что произойдет, если будет искажен второй символ в кодовой комбинации? Тогда комбинация 000 станет комбинацией 010, находим её в верхней строчке и видим, что она стоит от комбинации 000 на два уровня правее, что мы и отмечаем.

А теперь рассмотрим ошибку в первом символе, то есть крайним справа. В этом случае комбинация 000 будет преобразована в комбинацию 001. Находим эту комбинацию в верхней строчке, это комбинация, которая расположена рядом (справа, 1 шаг), что соответствует искажению или ошибке при восстановлении на один уровень, что мы и записываем.

Итак, мы получаем следующий результат: искажения 3-го, то есть крайне левого символа в кодовой комбинации приведет к ошибке в четыре уровня искажения, 2-го символа в кодовой комбинации приведет к искажению на два уровня, искажения первого символа, то есть крайне правого изменит комбинацию на 001, что соответствует искажению на один уровень.

Теперь надо повторить все те же рассуждения для следующей кодовой комбинации, а именно 001. Рассмотрим сбой крайне левого символа. В нашем понимании это третий символ, поскольку здесь мы считаем справа налево. Значит, комбинация 001 станет комбинацией 101. Несложно увидеть, что в этом случае ошибка будет на 4 уровня, что мы отмечаем. Ошибка во 2м символе приведет к искажению на два уровня. Наконец, если будет искажен первый символ, то есть крайний правый, то комбинация 001 станет комбинацией 000, а это соответствует отличию на один уровень, что мы видим исходя из верхней строчки. Если продолжить подобные рассуждения в отношении всех других кодовых комбинаций, то мы увидим, что во всех случаях мы получаем один и тот же спектр - будем употреблять такой термин.

Подводим итог: искажения в 4 уровня встречается 8 раз, прибавляем к этому искажении в 2 уровня, которые тоже встречаются 8 раз и прибавляем к этому искажения на 1 уровень, которые тоже встречаются в 8 раз. Тогда получаем цифру искажений 56, учитывая, что можно считать равновероятным сбой как первого, так и второго, так и третьего уровня. Подобного рода суммирования будут оправданы во второй и в третьей строчке.

Мы представляем варианты различных двукратных ошибок, это указано в левом столбце. Когда искажается сразу и 3й, и 2й символ кодовой комбинации. Далее вариант, когда искажается сразу 2й и 1й символ кодовой комбинации. Наконец, третий вариант из всех возможных, когда сразу искажается 3й и 1й символы в кодовой комбинации. Других вариантов не может быть.

Рассмотрим кодовую комбинацию 000, если искажен 3й и 2й символ, значит комбинация станет 110. В верхней строчке обнаруживаем эту комбинацию, видим, что от исходной кодовой комбинации она отстоит на 6 уровней, пишем цифру 6. Рассматриваем следующий вид сбоя, когда искажается 2й и 1й символ, тогда кодовая комбинация 000 преобразуется в комбинацию 011. Находим эту кодовую комбинацию в верхней строке, видим, что она стоит от кодовой комбинации 000 на 3 уровня правее, что мы и отражаем в соответствующем столбике. Наконец, рассматриваем сбой 3го и 1го символа, комбинация 000 станет комбинацией 101. Находим эту комбинацию в верхней строке, видим, что она стоит на пять уровней правее. Таким образом, в итоге мы записываем, что при разных вариантах двукратных сбоев мы получаем искажения на 6 уровней квантования, на 3 уровня квантования, на 5 уровней квантования.

Продолжая подобные рассуждения, получаем спектры ошибок для всех двукратных сбоев. По сравнению с предыдущими вариантами ошибок, здесь значительно больше разнообразия. В итоге спектр можно отобразить так, как это сделано в крайнем столбце. Мы видим, что в данном случае искажения в 6 уровней встречаются четыре раза, к этому прибавляются искажения в 5 уровней, которые также встречаются 4 раза искажение в 3:00 уровня встречаются в 8 раз искажения в 2:00 уровня встречаются четыре раза и искажения в 1 уровень, которые также встречается 4 раза.

Полагая, что все варианты сбоев равновероятны, мы получаем итоговую сумму равную 80. Последняя строчка данной таблицы соответствует ситуации, когда искажены все три символа. Проведем обсуждения в отношении комбинаций 000 при искажении всех трёх символов. Комбинация 000 превратиться в 111, что соответствует искажению в 7 уровней. Если мы рассмотрим комбинацию 001, то искажения всех трёх символов приведет к комбинации 110, находим эту комбинацию в верхней строке, видим, что 110 от исходной комбинации 001 отстоит на 5 уровней, что мы и записываем.

Аналогично получаются все остальные цифры - итоговый результат, который представлен в крайней правой колонке: 7 уровней искажается в двух случаях, 5 уровней также в двух случаях, мы имеем искажения на 3 уровня в двух случаях и на 1 уровень также в двух случаях. Всего происходит искажений на 32 уровня. Надо отметить, что здесь мы приняли условности, состоящее в том, что все случаи искажения символов в кодовых комбинациях равновероятны. Поэтому мы использовали простое арифметическое суммирование.

На самом деле в каналах связи помехи приводят к различным ошибкам с различной вероятностью. Если учитывать это обстоятельство, то нам надо находить не арифметическое среднее, а математическое ожидание. Каждому искажению будет присваиваться своя вероятность возникновения этого искажения, что сделает расчёты более громоздкими и сложными. В нашем же случае нам важно разобраться с тем, как разные способы кодирования приводят к различным результатам по искажениям кода.

В итоге натуральный код был нами разобран, мы получили для него спектр ошибок при различных однократных сбоях, при различных двукратных и трехкратном сбоях. Помимо этого кода, можно рассмотреть и другие: код Грея, код в импульсно-кодовой модуляции (ИКМ), код МИ-2, МИ-3, случайный код и т.д. Рассмотрим примеры в таблицах 14-18.

Итак, код Грея кодирует уровни квантования следующим образом: 000, 001, 011, 010, 110, 111, 101, 100.

Таблица 14 – Код Грея

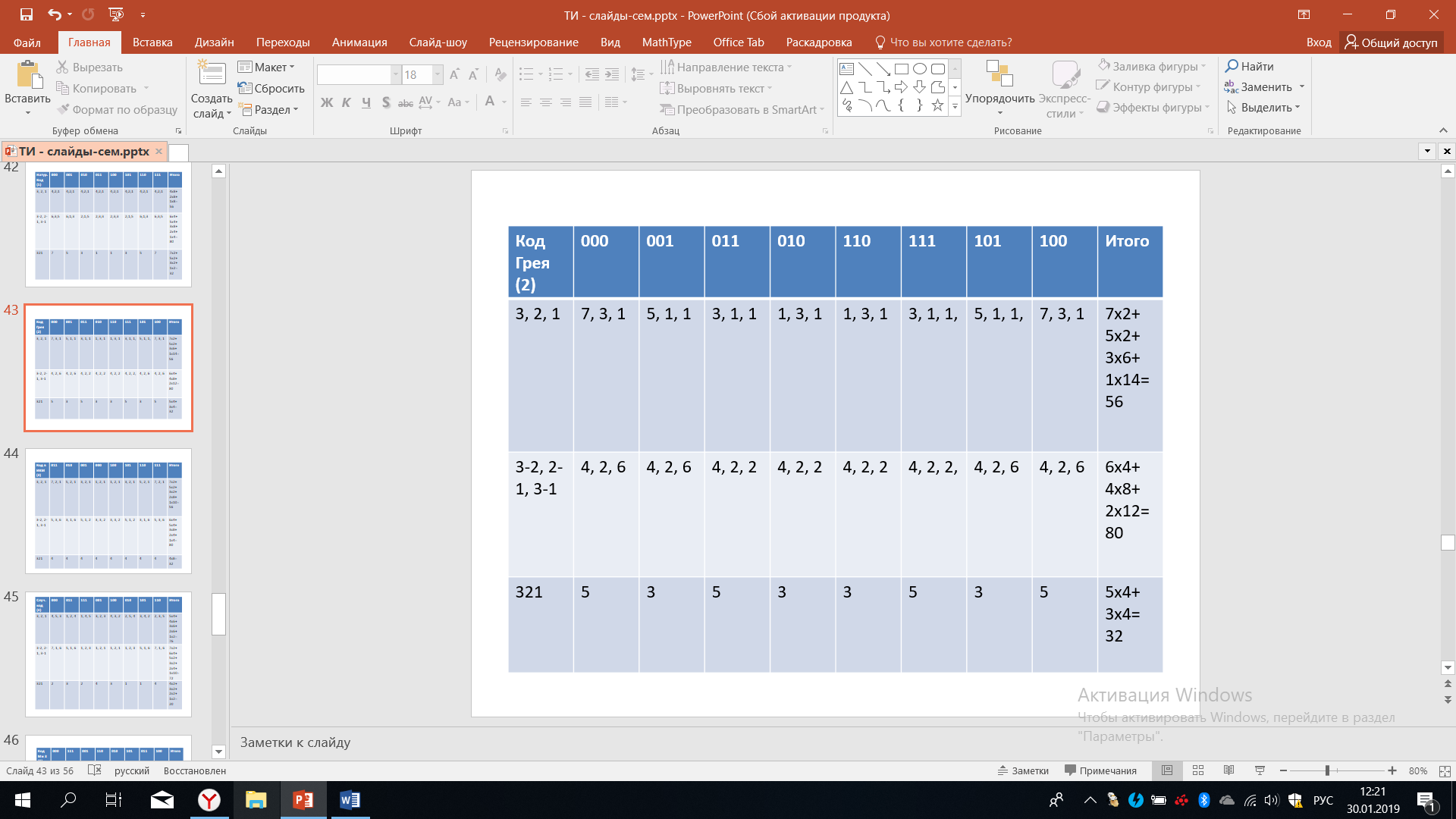
Рассмотрим код в ИКМ - это тот вариант, который был рассмотрен при аналого-цифровом преобразовании. Он кодирует уровни квантования, как 011, 010, 001, 000, 100, 101, 110, 111.

Таблица 15 – Код в ИКМ

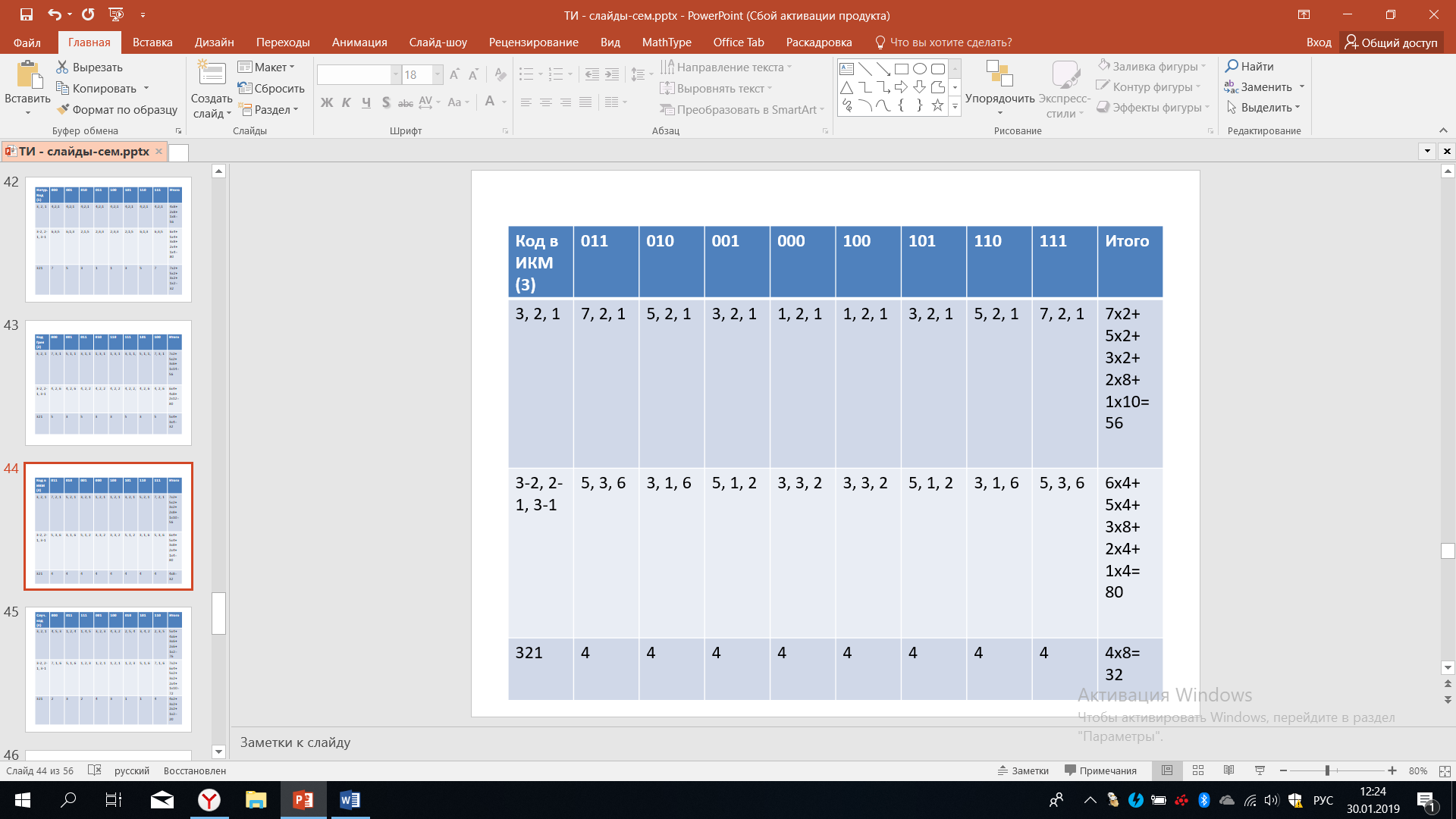
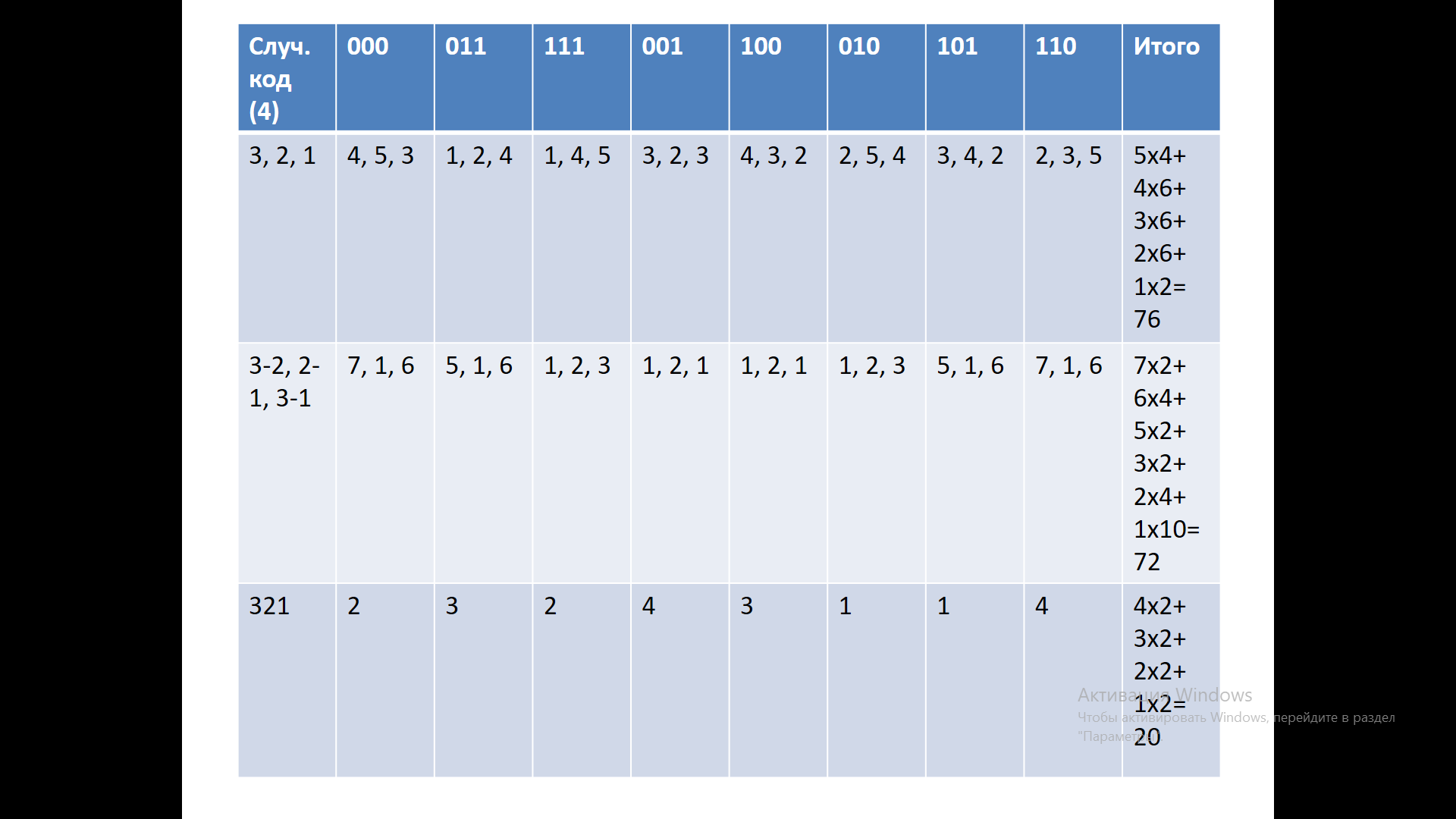
Рассмотрим еще один вариант, назовем его случайный код. Случайный он потому, что наугад была выбрана последовательность кодовых комбинаций: 000, 011, 111, 001, 010, 101, 110.

Таблица 16 – Случайный код

Как мы уже не раз отмечали, количество различных вариантов кодирования очень быстро нарастает с увеличением длины кодовой комбинации. Даже при 3-символьной кодовой комбинации это число равное (8)! исключительно велико. Если вычислить это выражение, то это будет 40320 различных вариантов. Для особо любопытных можно предложить посчитать и другие значения числа вариантов кодирования. При большем n очень быстро нарастает число различных вариантов. Тем не менее можно применить определенные усилия и найти некоторые хорошие кодовые комбинации, хорошие решения, что является нетривиальной задачей. В данном случае мы не будем этим заниматься, просто запомнив, что всегда можно найти самый хороший вариант.

Теперь рассмотрим следующий код, который мы назовем МИ-3, а предыдущие рассуждения нам помогут. Мы понимаем, что это код, для которого ошибка при искажении 3-х символов будет минимальна, поэтому этот код назвали МИ-3. Итак, для данного кода характерно то, что кодовые комбинации, отличающиеся друг от друга на три разряда, располагаются буквально рядом: 000, 111, 001, 110, 010, 101, 011, 100.

Таблица 17 – Код МИ-3

Этот вариант интересен тем, что при таком варианте кодирования искажения минимальны в случае трехкратный сбоев, для однократных и двукратных сбоев эти искажения имеют спектр, который показан в крайнем правом столбике. Мы чуть позже сравним все эти варианты кодирования и попробуем сделать некоторые выводы.

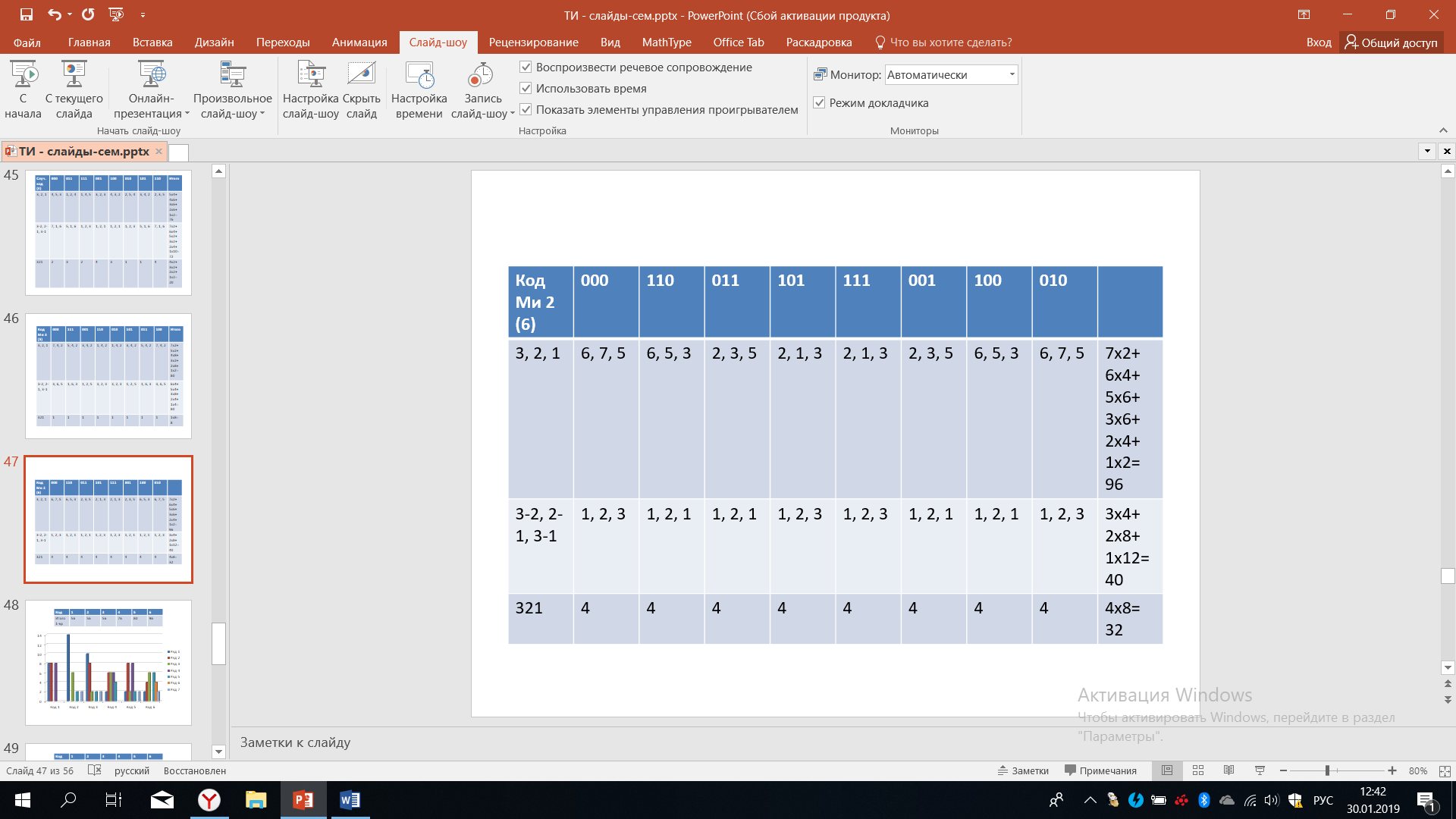
Пока что рассчитаем еще один вариант кодирования, который мы назвали МИ-2. При этом варианте кодирования минимальными будут искажения при двукратных сбоях, поэтому МИ-2 для всех других случаев искажения будут иметь то значение, которое получается после расчётов исследования, которые мы уже многократно делали. Итогом является то, что показано в крайне правой части этой таблицы.

Таблица 18 – Код МИ-2

Подведем некоторые итоги: при рассмотрении 6 вариантов кодирования на рисунке 46 представлены результаты в отношении однократных сбоев. В верхней таблице мы видим итоговый результат, что однократные сбои при первом способе кодирования в сумме приводят к 56 искажениям, для 2го и 3го варианта тот же результат, для 4го варианта - 76, для 5го ещё больше - это 80, и наконец, для 6го варианта искажения достигает 96 единиц. В этом смысле 6-й вариант наименее предпочтителен. На рисунке 46 также представлено распределение спектров.

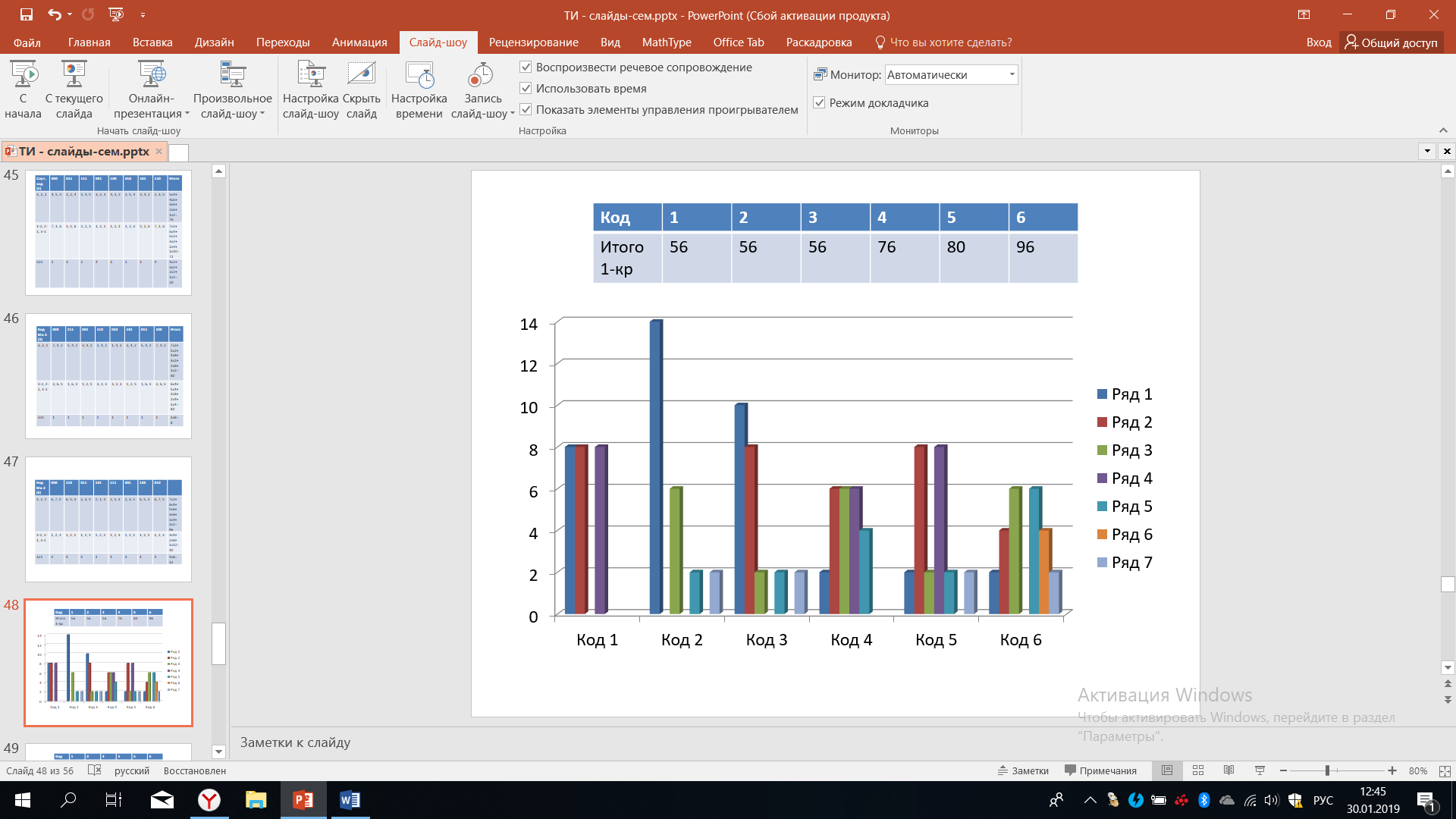
Рисунок 46 – Анализ однократных ошибок

Для кода номер один мы видим, что спектр его достаточно равномерный и искажения величиной в один уровень встречаются 8 раз, в два уровня встречаются тоже 8, в три уровня также встречаются 8 раз. Для кода номер два искажения в один уровень встречаются 14 раз, искажения в три уровня встречается 6 раз, искажения в пять уровней встречаются дважды и искажения в семь также встречаются дважды.

Для сравнения вот эти данные несут достаточно большую информацию, мы можем оперировать ими в случае различных распределений вероятностей, которые могут характеризовать тот или иной поток ошибок. Например, когда мы считаем, что все случаи равновероятны, то мы можем вычислять среднее как среднеарифметическое. А если здесь имеют место не равновероятные процессы возникновения ошибок, то нам надо будет учитывать значения, которые здесь изображены, а также вероятность их возникновения. Обратимся к шестому коду, он наиболее разнообразен. Мы видим, что искажения на один уровень встречается дважды, искажения на два уровня встречаются 4 раза, искажения на три уровне встречаются 10 раз, искажения на четыре уровня в данном случае отсутствуют, искажения в пять уровней также встречается 6 раз, искажения шесть уровней 4 раза, искажения в семь уровней встречаются дважды.

При этом присутствует даже определенная симметрия относительно искажения в четыре уровня. Итак, мы должны увидеть, что разные способы кодирования имеют очень разные спектры искажений, получаемых при одном и том же характере ошибок. Это должно подталкивать нас к поиску наилучших способов кодирования. Действенно, при тех условиях о которых мы должны знать заранее, то есть мы должны заранее знать, какой характер имеют возникающие ошибки, тогда можно провести точную оценку.

На рисунке 47 представлены спектры ошибок в случае различных двукратных сбоев для всех рассмотренных кодов из 40320 возможных вариантов. Даже эти коды, как мы видим, отличаются друг от друга. Для каждого кода имеются свои особенные спектры. Выбирая тот или иной способ кодирования, мы должны знать распределение ошибок и, воспользовавшись этим, можно провести точную оценку того, для какого способа кодирования ошибка будет минимальной.

Рисунок 47 – Анализ двукратных ошибок

На рисунке 48 представлены результаты возникших искажений для шести рассмотренных кодов в случае трехкратных ошибок. В данном случае мы видим, что первый код обладает самым разнообразным спектром искажения, коды номер три, пять и шесть наименее разнообразны в этом смысле, причём наилучший результат в коде номер пять. Для этого кода все возможные искажения равны единице, максимальные искажения возникают для кода номер один - там возможно искажения в 7 единиц, то есть на 7 уровней и это возможно в двух случаях из восьми возможных вариантов. Точный анализ и точный результат по выбору кодов можно получить, зная точное распределение ошибок.

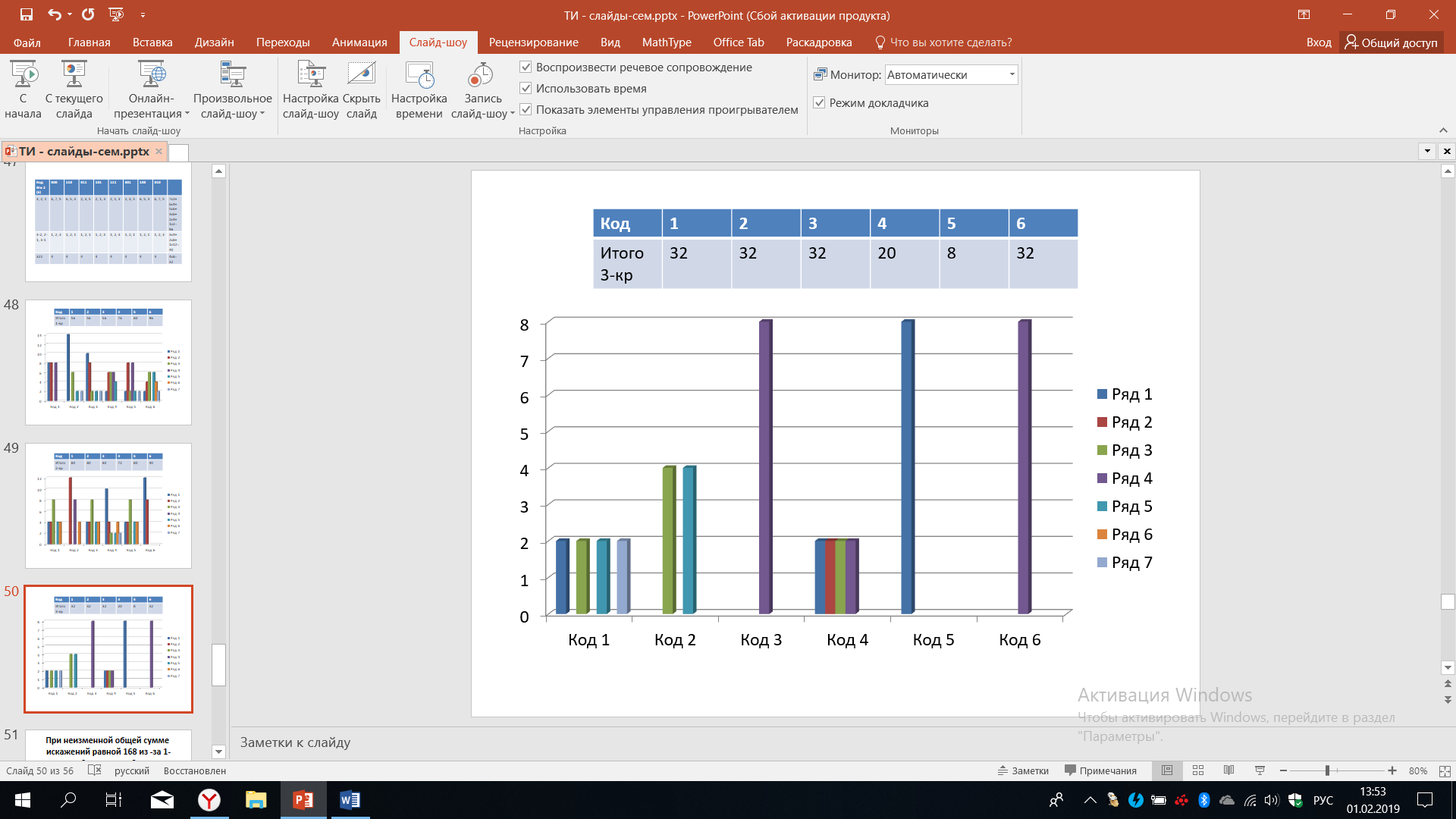
Рисунок 48 – Анализ трехкратных ошибок

Подведем предварительный итог: рассмотрению 6 вариантов кодирования, можно доказать, что в этом случае общая сумма различных искажений неизменно равна 168 из-за всех возможных однократных, двукратных и трехкратных сбоях или ошибок. Всего может быть, как уже не раз отмечалось, 40320 различных вариантов кодирования.

Таблица 19 – Численные данные анализа ошибок кодирования

Код	1	2	3	4	5	6
1-кр	56	56	56	76	80	96
2-кр	80	80	80	72	80	40
3-кр	32	32	32	20	8	32

Численные данные представлены в таблице 19, с помощью них можно попробовать подвести некие предварительные итоги.

Начнем с самого простого при n=1 мы имеем всего две кодовых комбинаций 0 и 1. Матрица кодовых расстояний D₁ строится следующим образом: верхняя строчка - это расстояние между кодовыми комбинациями. Очевидно, что кодовое расстояние между нулем и нулем равно нулю. Кодовое расстояние между нулем и единицей равно единице, что отражается в верхней строчке матрицы кодовых расстояний. Вторая строчка строится путем сравнения кодовой комбинации один соответственно с нулевой и с единичной.

Итак, при сравнении единицы с нулём - кодовое расстояние равно единице, при сравнении единицы с собой кодовое расстояние равно нулю. Мы получили очень простую матрицу кодовых расстояний.

Первая строчка матрицы кодовых расстояние D₂ строится путем сравнения первой кодовой комбинации - 00 вначале с собой, а затем со всеми остальными – 01,10,11. Итак, при сравнении 00 с самой собой расстояние равно нулю, 00 сравнивается с кодовой комбинации 01 - кодовое расстояние равно единице, кодовая комбинации 00 сравнивается с 10 - кодовое расстояние равно единице, 00 сравнивается с комбинацией 11 - кодовое расстояние между ними равно двум. Поэтому первая строчка матрицы кодовых расстояний 0-1-1-2.

Вторая строчка получается путем сравнения второй кодовой комбинации 01 последовательно со всеми: 01 сравнивается с 00, имеем кодовое расстояние равное единице, потом кодовая комбинация сравнивается сама с собой - кодовое расстояние равно нулю, далее 01 сравнивается с 10 и кодовое расстояние равно двум, наконец 01 сравнивается с 11 - кодовое расстояние равно единице. Мы получаем вторую строчку матрицы кодовых расстояний 1-0-2-1.

Третья строчка получается путем сравнения третьей кодовой комбинации 10 последовательно со всеми: 10 сравнивается с 00 - кодовое расстояние равно единице, 10 сравнивается с 01 - кодовое расстояние равно двум, кодовая комбинация сравнивается сама с собой - кодовое расстояние равно нулю, наконец, 10 сравнивается с 11 - кодовое расстояние равно единице. Мы получили третью строчку матрицы кодовых расстояний 1-2-0-1.

Теперь кодовая комбинация 11 сравнивается последовательно со всеми кодовыми комбинациями: сначала с кодовой комбинацией 00 - строчка начинается с цифры 2, далее 11 сравнивается с 01 - между ними отличие в одном разряде, при сравнении 11 с 10 также кодовое расстояние равное единице, и, наконец, 11 сравнивается сама с собой - кодовое расстояние равно нулю. В итоге нижнее завершающая стручка матрицы кодовых расстояний 2-1-1-0.

После определенного анализа и достаточно простых наблюдений, можно в общем виде записать рекуррентную формулу для построения матрицы кодовых расстояний при любом n.

В общем виде имеем:

где

Если мы посмотрим на матрицу D₂, то мы видим, что это правило очень четко выполняется при построении из матрицы D₁. Действительно верхний левый угол - это матрица D₁, нижний правый угол - это матрица D_1, правый верхний угол - это матрица D₁, где все элементы увеличены на единицу, наконец, нижний левый угол - это тоже матрица D_1, увеличенная на 1.

Вот такое интересное правило построения матрицы кодовых расстояний. Эта матрица замечательна тем, что в ней представлены все возможные кодовые расстояния, которые существуют при сравнении всех возможных кодовых комбинаций между собой. Из-за ошибок в канале связи одно сообщение может быть принято, как другое сообщение, в этом случае говорят, что возникают потери информации. Потери информации удобно отразить в виде матрицы потерь, где числа L_i,j, стоящие в матрице, означают потери в случае ,если это сообщение будет принято как другое.

В данный матрице мы видим числа l₁₁, l₂₂ и так далее. В нашем определение это соответствует тому, что первое сообщение будет принято, как первое - это l₁₁ или второе сообщение будет принято, как второе это l₂₂. Вполне логично положить эти числа равными нулю, поскольку при этом никаких потерь не происходит. Следовательно, в этой матрице потерь на главной диагонали будут располагаться нули. А все остальные это числа, характеризующие потери, например, l₂₁ - это потери в том случае, если второе сообщение будет принято как первое сообщение, l₁₂ - это потери, если первое сообщение будет принято как второе.

В общем случае l₁₂ может не совпадать с l₂₁, хотя довольно часто оказывается, что матрица потерь имеет симметрию относительно главной диагонали, тогда l₁₂ будет равно l₂₁, l_1n будет равно l_n1 и т.д. Но в общем случае это далеко не так. Например, вам передаётся первое сообщение о том, что вы заработали 100 руб. и второе сообщение о том, что вы заработали 1000 руб. Эти сообщения передаются, например, в кассу, где вы должны получить эти деньги. Если произойдет ошибка и вместо первого сообщения будет принята второе, то вам в кассе выдадут вместо 100 руб. 1000 руб., а если второе сообщение будет принято как первое, то вам выдадут вместо 1000руб. -100 руб. Попробуйте оценить и в первом и во втором случае те потери, которые возникнут у банка, выдающего эти деньги и возможные потери для вас, как человека, который в одном случае получит излишние деньги, а в другом случае не получит честно заработанные деньги.

Данный пример говорит о том, что определение матрицы потерь - это очень непростая задача, но исключительно важная для того, чтобы можно было оценивать и выбирать наилучшие способы кодирования, о которых мы говорили. Зачастую оценкой является средние потери, которые можно рассчитать по формуле, приведенной ниже:

где p_i - это вероятность возникновения той или иной ошибки, приводящей к тем или иным потерям; l_i,j - потери, которые будут происходить; матрица условных вероятностей о том, что будут принято сообщение a_j*при условии, что передавалось сообщение a_i.

Для лучшего понимания и наглядности при различных исследованиях и выборах наилучших вариантов кодирования или вариантов каких-либо других преобразований, удобно рассматривать векторное представление тех сложных процессов, которые происходят. Удобно осуществлять анализ элементов разложения этого сложного процесса. Часто мы используем для этого достаточно наглядные представления в метрическом соответствии с теми определениями, которые мы сейчас с вами вспомним.

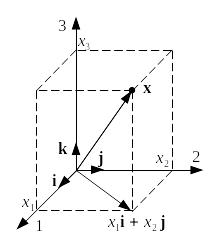
Рисунок 49 – Векторное представление

На рисунке 49 изображено то пространство, которое характерно для часто используемых нами примеров. Для того чтобы проводить сравнение количественных оценок, нам необходимо ввести метрику или расстояние между элементами данного пространства, элементами данного множества. Эти элементы должны удовлетворять аксиомам, которые представлены ниже.

Метрическое пространство. Пусть задано множество произвольных элементов – векторов сигнального пространства. Множество называется метрическим пространством, если для каждых двух произвольных элементов , этого множества введена неотрицательная функция , называемая метрикой или расстоянием, которая удовлетворяет следующим аксиомам:

а) только тогда, когда ;

б) - аксиома симметрии;

в) - аксиома неравенства треугольника для расстояния.

Если вспомнить матрицу потерь, о которой мы говорили ранее, то в общем отдельные особенности этой матрицы потерь могут не совпадать с тем, что мы только что определили.

Мы каждый раз должны их оценить на предмет адекватности тем реальным сообщениям, которые передаются, насколько принимаемое нами соответствует той реальности, которая присутствует при описании или оценки тех или иных сообщений.

Разберем несколько примеров. Мы знаем о матрице потерь, рассмотрим некоторые случаи, когда мы имеем дело с четырьмя сообщениями, расстояние между которыми А. Это расстояние можно отождествить с потерями, расстояние между которыми оценивается геометрическим расстоянием между вершинами квадрата. При этом сторона квадрата равна l.

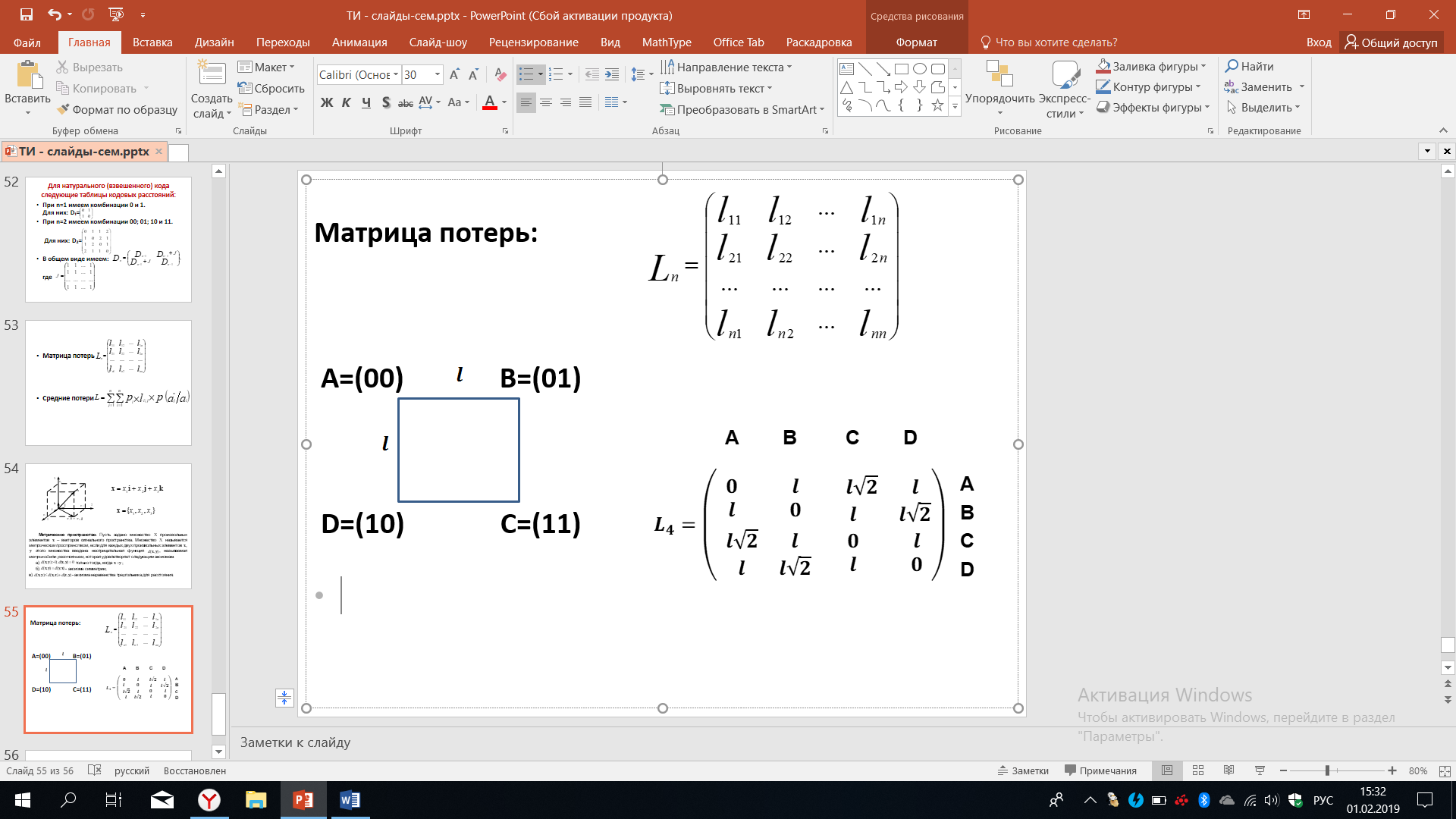
Рисунок 50 – Квадрат потерь при передаче сообщений

Мы видим, что для данного случая матрица потерь примет вид, показанный ниже. Кодовое расстояние или потери между A и A равны нулю, между B и A – l.

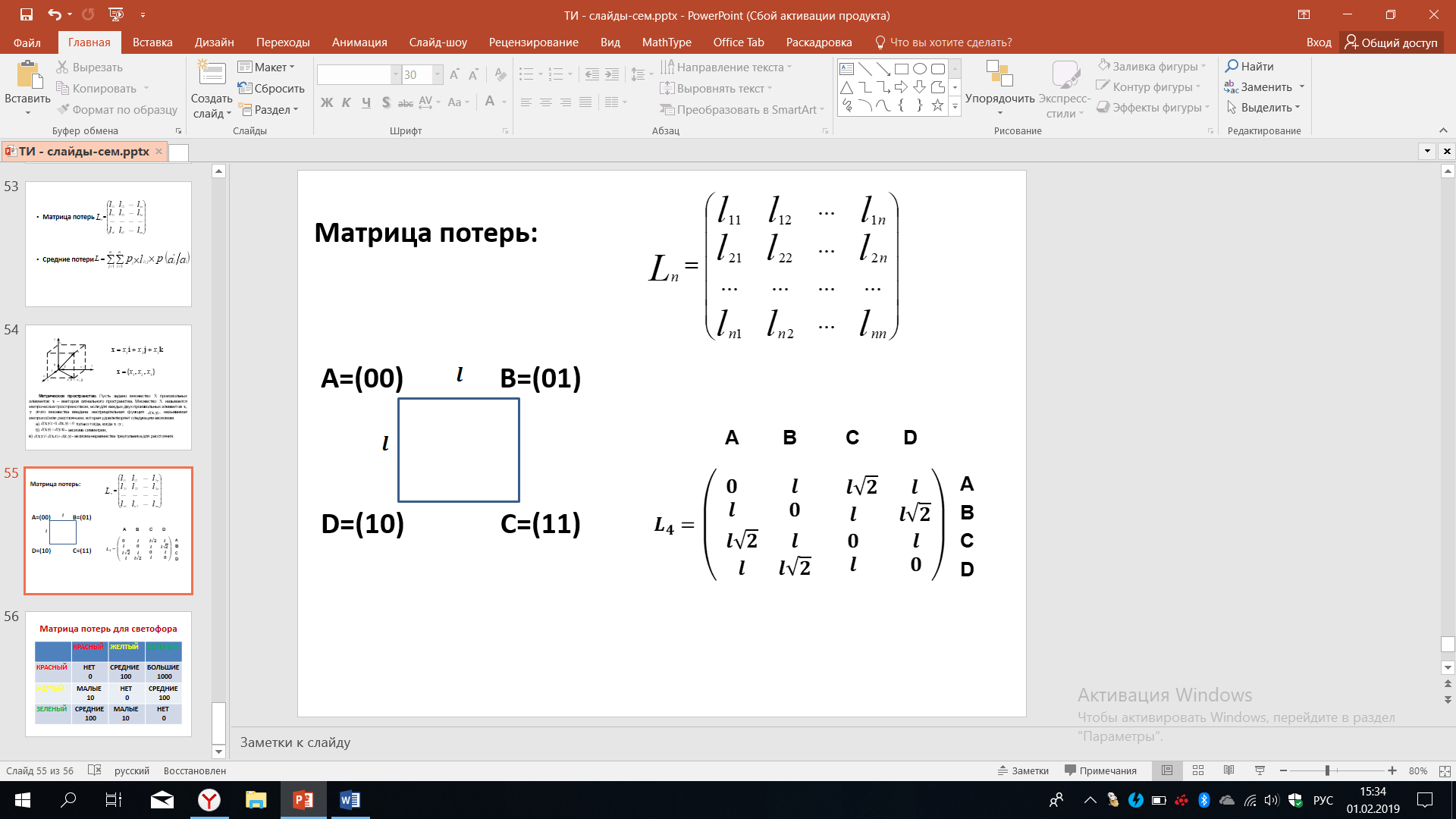
Расстояние между точкой C по отношению к A определяется диагональю данного квадрата и очевидно равно . Из подобных геометрических рассуждений вычисляются все значения для данной матрицы потерь, когда мы договариваемся, что количественным показателем потерь будут являться геометрические расстояние между соответствующими точками. Другими словами, мы отождествляем расстояние с потерями, то есть чем больше расстояние, тем больше потери. Мы строим матрицу потерь.

Рассмотрим еще один случай различных сообщений и, соответственно, построение матрицы потерь. Итак, нашими сообщениями будут различные цвета, которые загораются на светофоре - это всем известный красный, жёлтый и зелёный цвета. Если красный цвет должен был зажечься, и он зажегся, значит никаких потерь нет. Мы будем это отражать в нашей матрице потерь, записав слова НЕТ. Если жёлтый будет принят как жёлтый, потерь нет, мы записываем слово НЕТ. Если должен был загореться зелёный и загорелся зелёный, то опять же потерь нет.

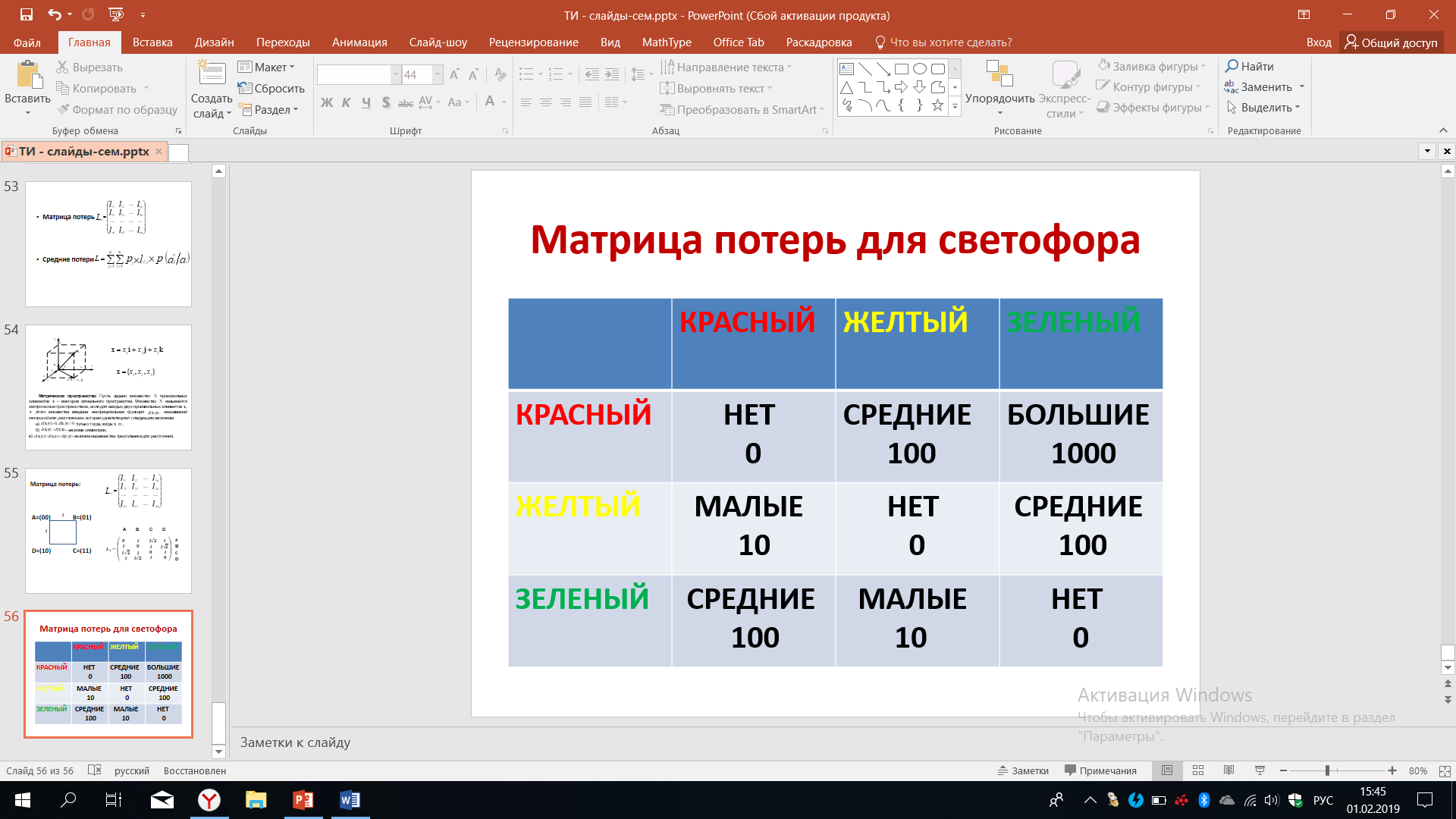
Рисунок 50 – Матрица потерь светофора

Теперь представим себе, что должен был загореться красный и мы будем исследовать строчку, соответствующую красному цвету. Итак, следуя по этой строчке, рассмотрим события, если должен был загореться красный, а зажегся желтый. Оперируя некими общими соображениями, оценим потери, как средние. Если вместо красного будет гореть зелёный, то такие потери мы оценим, как большие. В этом случае могут наступить очень серьёзные последствия с авариями машин. Запишем это как большие потери.

Рассмотрим следующую строчку, когда должен был загореться желтый цвет, а загорается красный. Желтый цвет призывает водителей остановиться. Но если загорелся красный цвет, то этот призыв будет звучать ещё более явственно, в этом случае разумно потери оценить как малые. Если же вместо желтого загорится желтый, мы уже говорили, что потери нет. Если вместо желтого загорается зеленый, то, поскольку жёлтый предупреждает, но всё-таки не запрещает, как красный свет, появление зелёного цвета в данном случае можно оценить как средние потери.

Нижняя строчка соответствует той ситуации, когда должен был загореться зелёный цвет, а загорается красный. Эти потери оценим как средние, потому что зелёный цвет разрешает движение, а красный запрещает. Это означает, что машины вместо возможного движения получат сигнал о том, что им надо будет остановиться. Это неприятно для тех, кто едет, они много останавливаются, но каких-либо более серьёзных последствий при этом не будет. Если вместо зелёного загорается желтый цвет, то это малые потери по очевидным причинам. Наконец, если зелёный будет принят как зелёный, потери отсутствуют.

Оперируя такими общими понятиями, мы построили матрицу потерь. Однако для количественного оценивания нам нужны числа и здесь есть определенные условности, поскольку, присвоив понятиям средние, малые, большие то или иное число, мы будем получать разные количественные результаты. В зависимости от того, как будут эти присвоения осуществлены, как будет введена метрика, будет определено расстояние. Но мы можем договориться, в качестве примера, что большие потери будут оцениваться нами в 1000, средние в десять раз меньше (а именно 100) и малые потери ещё в десять раз меньше (число 10).

Тогда мы получим количественную оценку для матрицы потерь, уже после этого можно проводить количественные расчеты по выбору тех или иных методов кодирования с целью оптимизации. При этом обратим внимание на то, что вот в этой матрице потерь нет той симметрии, о которые мы говорили ранее. Жёлтый принимаемый как красный не соответствует тому, как красный принимается как жёлтый. Это пример того случая, когда матрица потерь не является симметричной относительно главной диагонали. Но надо согласиться с тем, что она адекватна той ситуации с источником дискретных сообщений, которую мы только что рассматривали. Энтропия максимальна.